How to Create Admirable Plots with rpact

Utilities

Sample size

Power

Power simulation

This document provides many different examples for creating plots with rpact and ggplot2.

Author

Friedrich Pahlke and Gernot Wassmer

Published

March 8, 2023

Preparation

First, load the rpact package

library(rpact)
packageVersion("rpact") # version should be version 3.0 or later

[1] '3.3.4'

Design plots

One-sided design with futility bounds

design <- getDesignGroupSequential(
    kMax = 3,
    typeOfDesign = "OF", sided = 1,
    futilityBounds = c(0, 0.1)
)

plot(design, type = 1)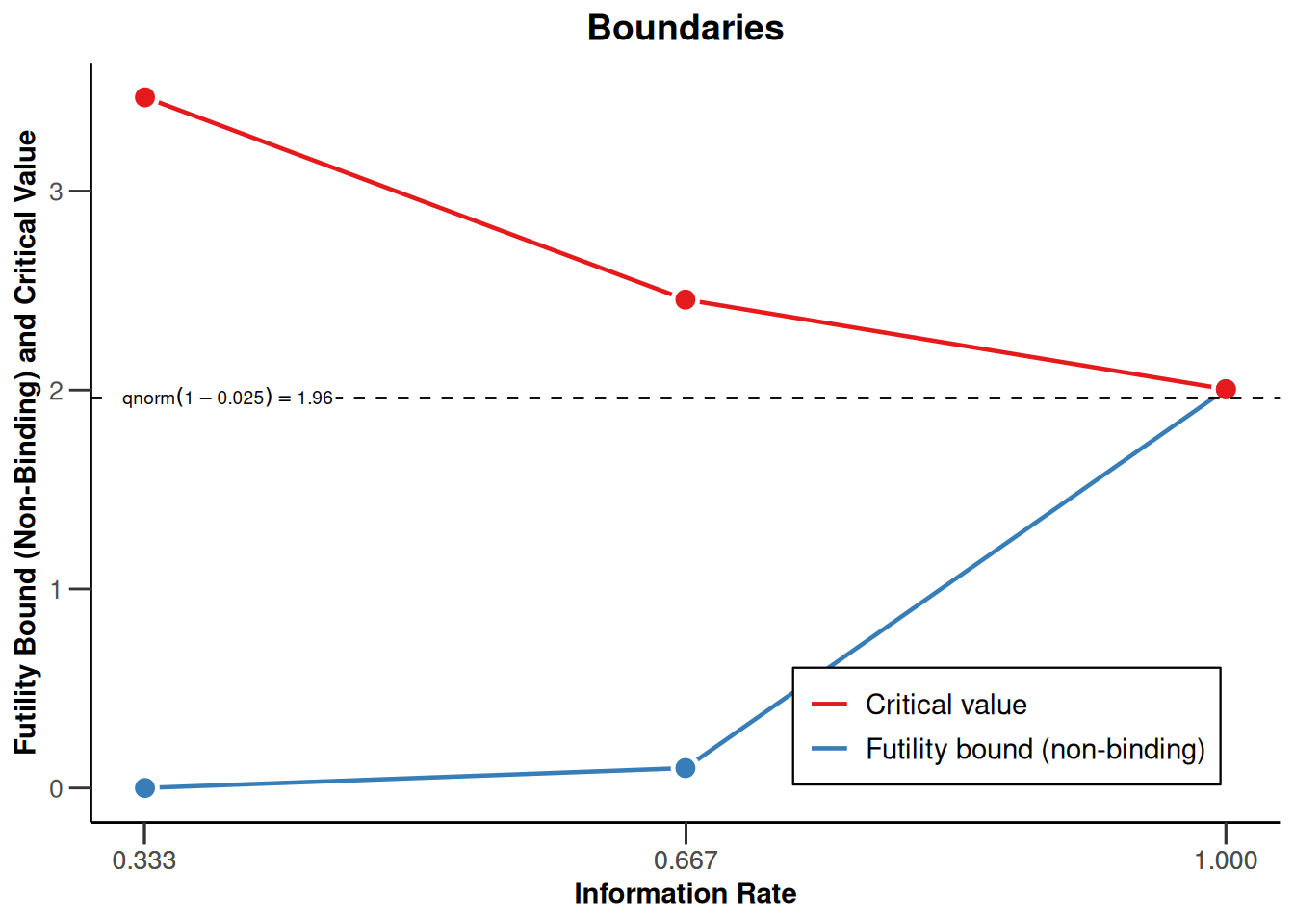

plot(design, type = 5, nMax = 10)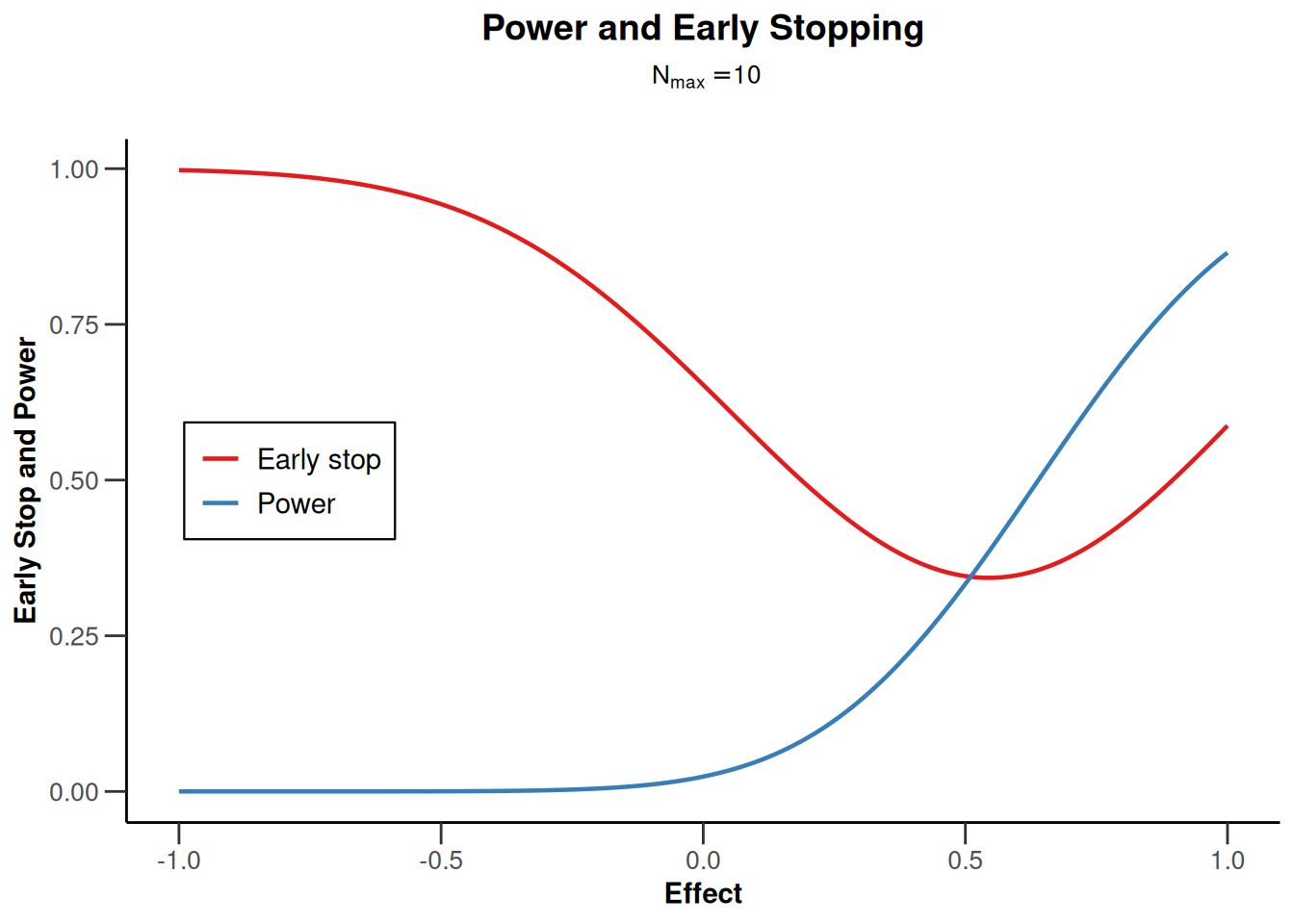

plot(design, type = 6, nMax = 10)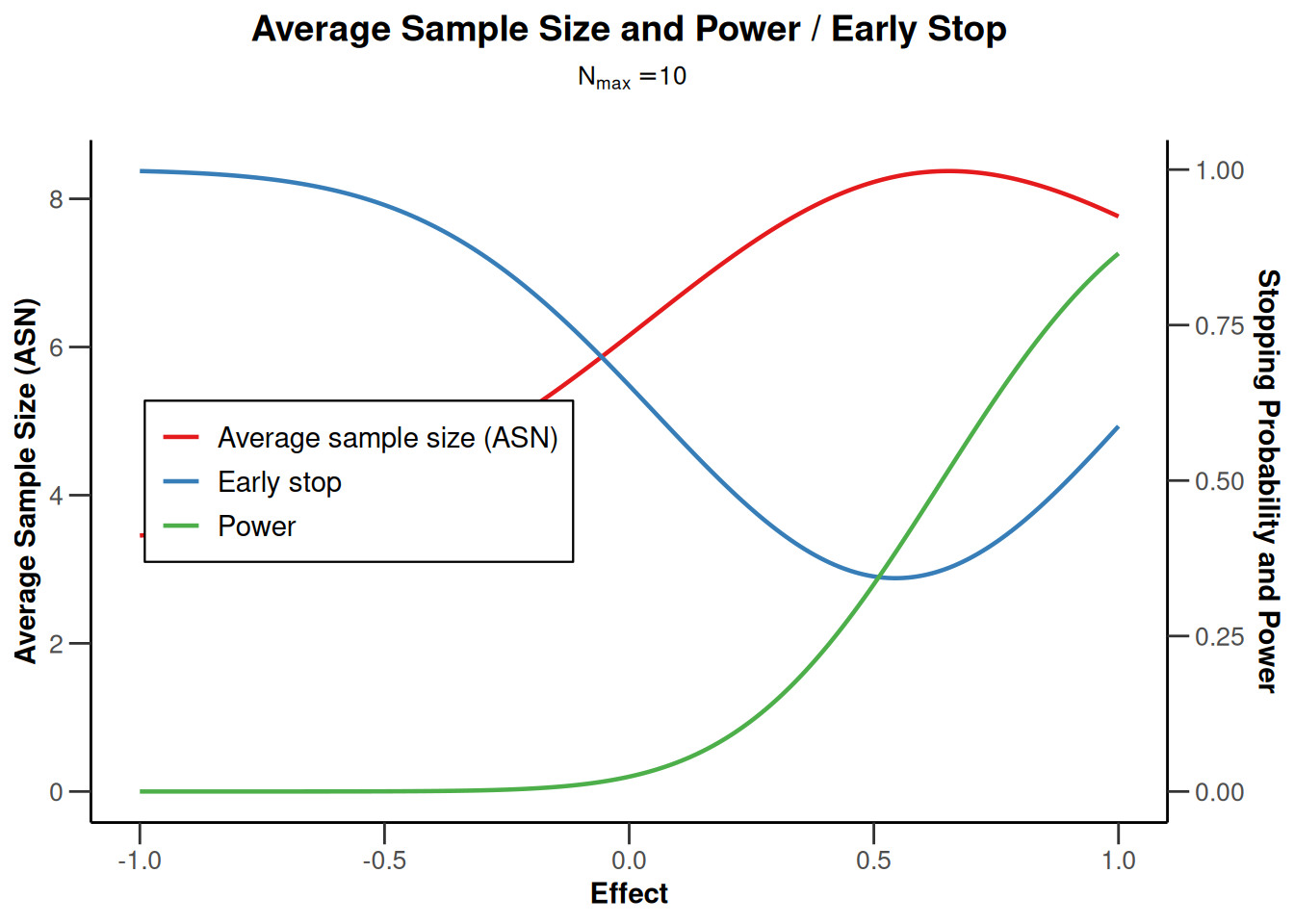

Two-sided design

design <- getDesignGroupSequential(
    kMax = 4, typeOfDesign = "OF", sided = 2, twoSidedPower = TRUE
)

plot(design, type = 1)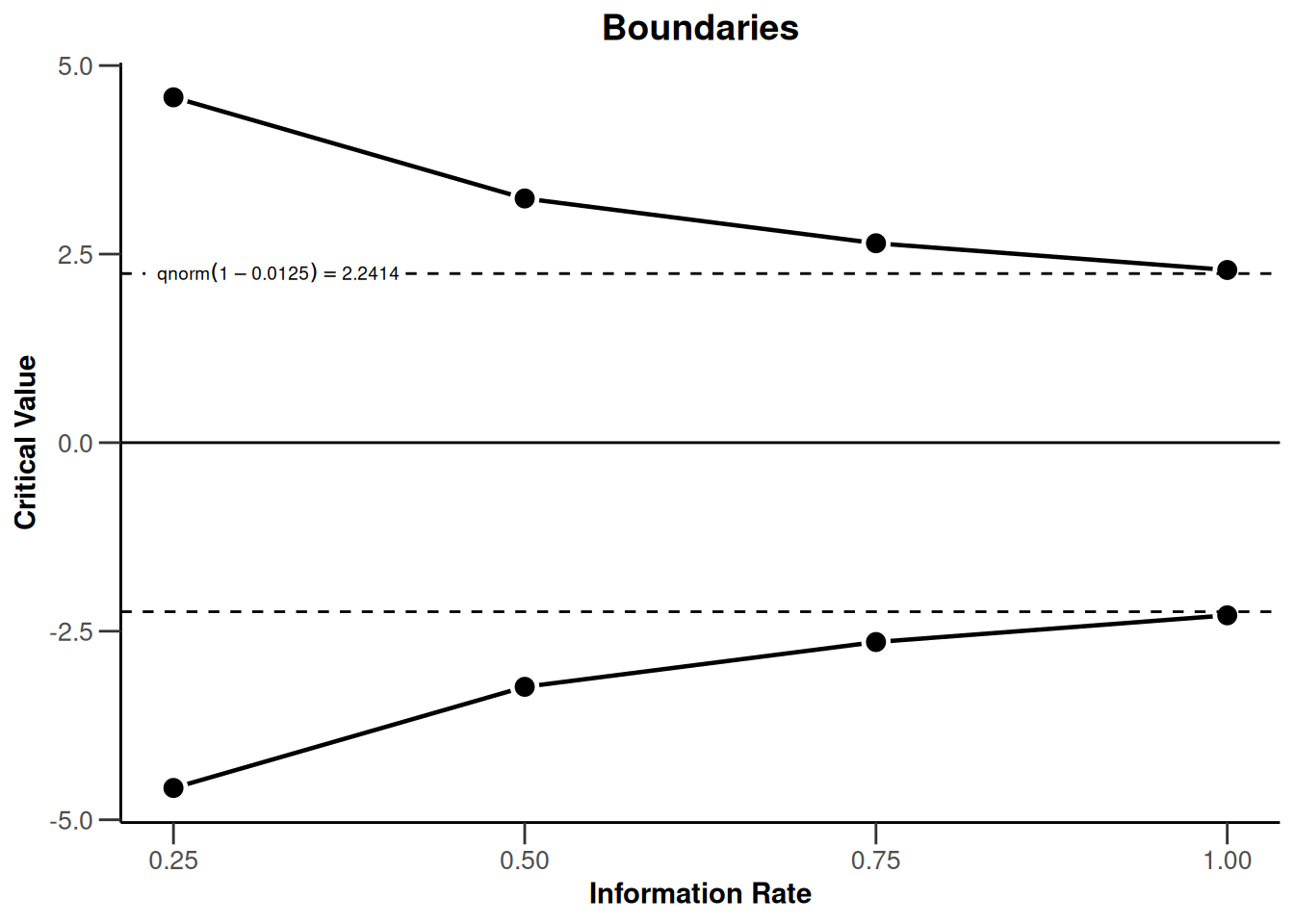

plot(design, type = 5, nMax = 10)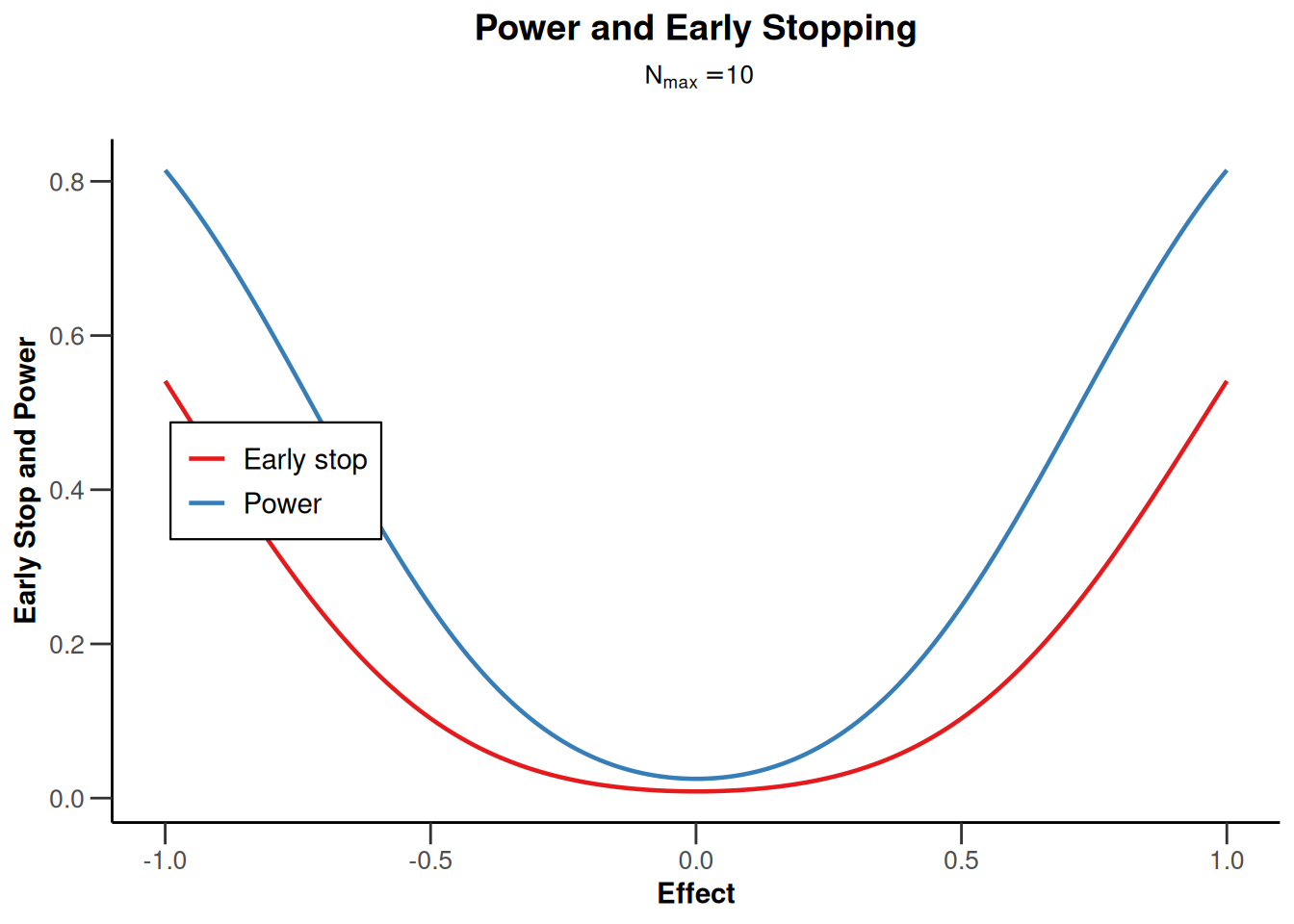

plot(design, type = 6, nMax = 10)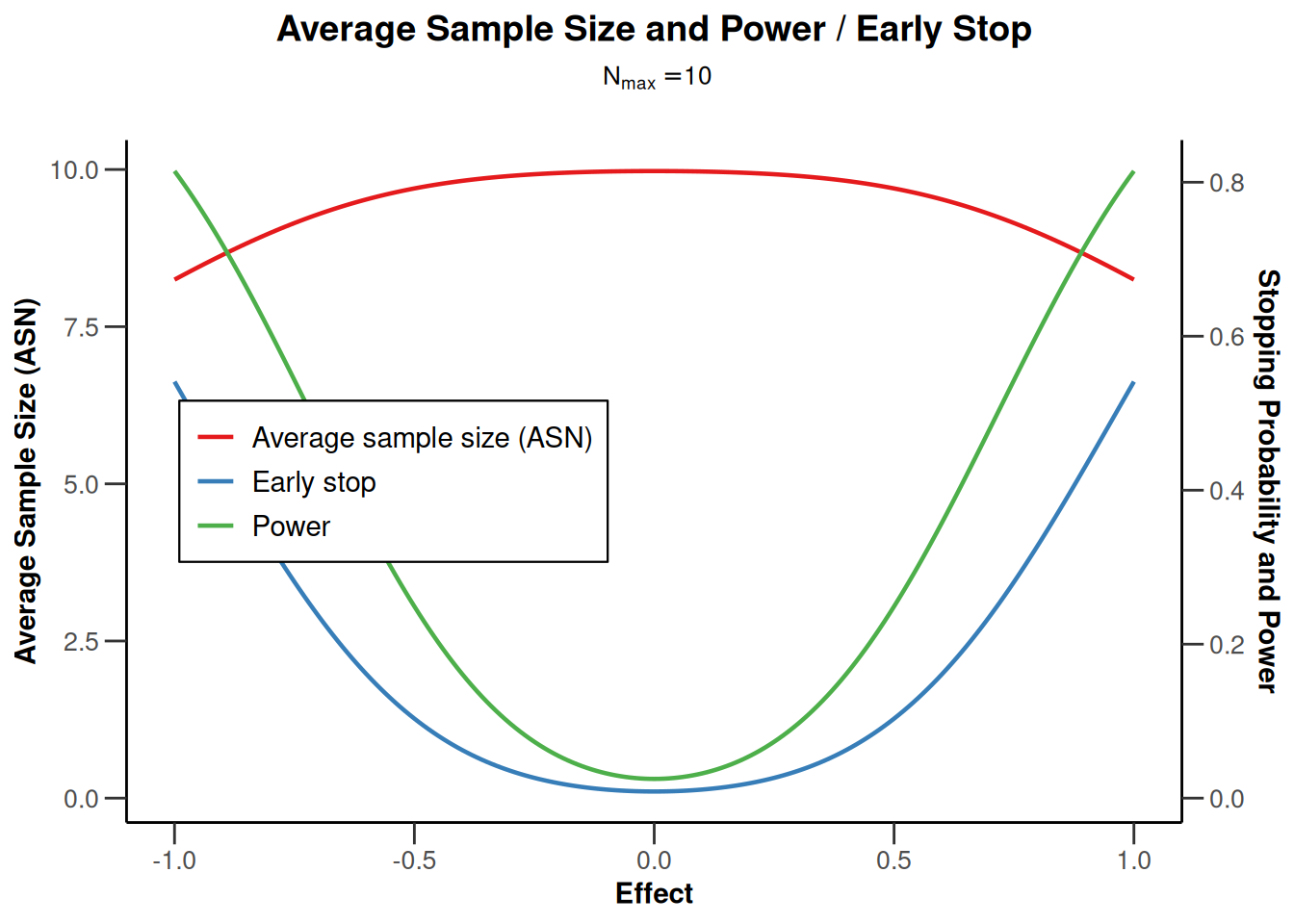

Two-sided design with futility bound

design <- getDesignGroupSequential(
    beta = 0.05, kMax = 4, typeOfDesign = "asOF",
    typeBetaSpending = "bsOF", sided = 2
)

Warning: The two-sided beta-spending approach is experimental and hence not
fully validated (see www.rpact.com/experimental)

plot(design, type = 1)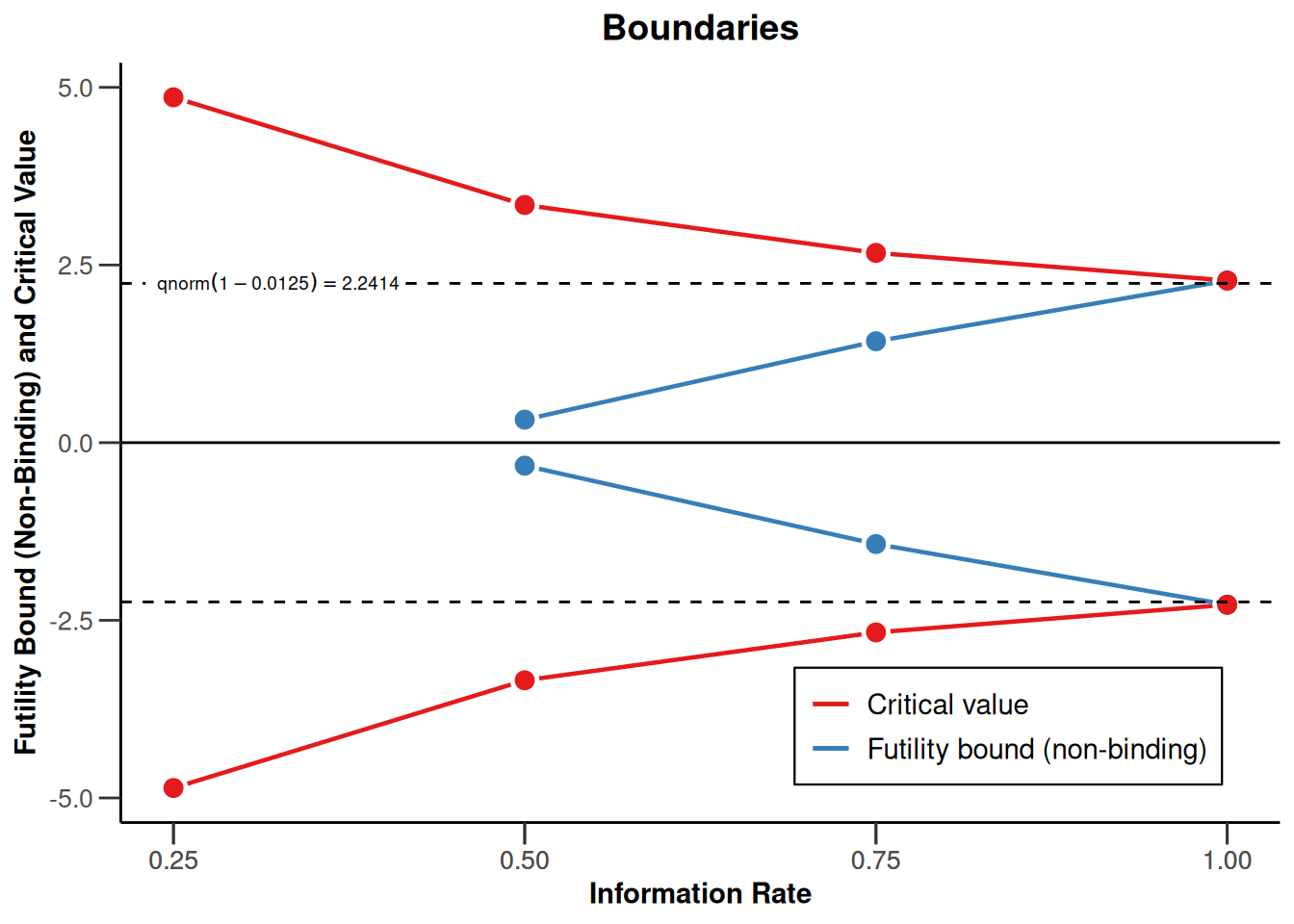

plot(design, type = 5, nMax = 10)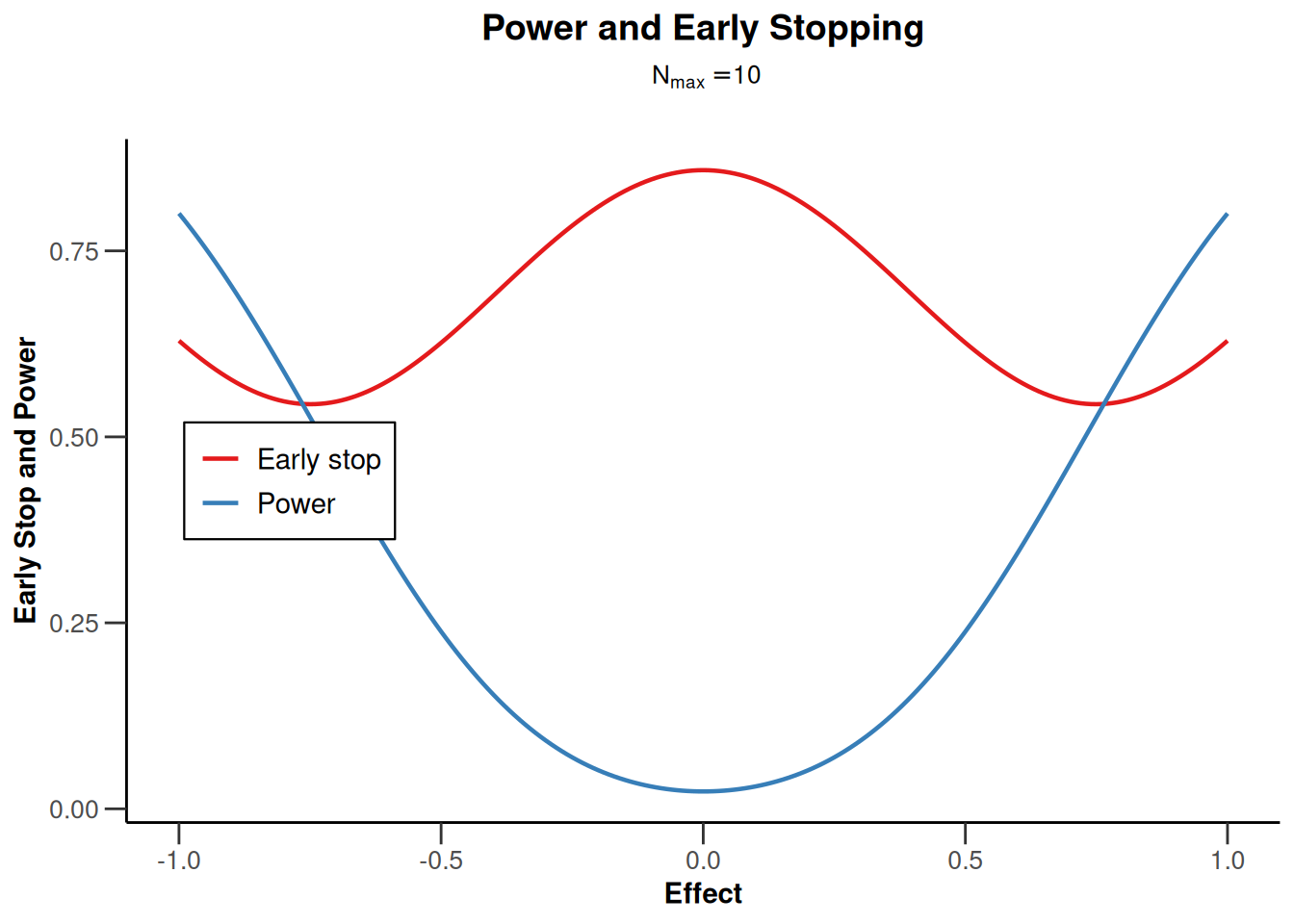

plot(design, type = 6, nMax = 10)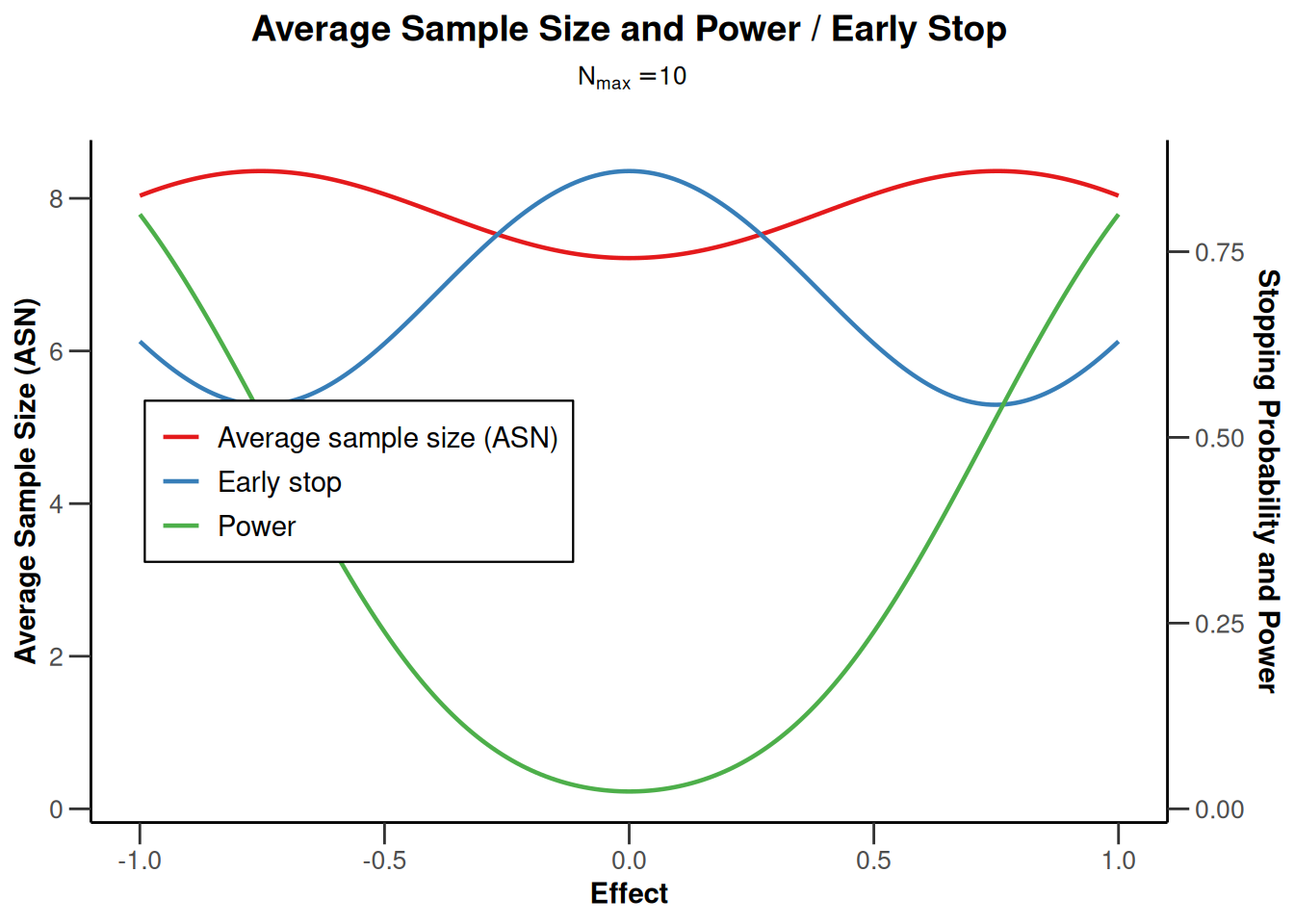

Sample size plots

Sample size means (continuous endpoint)

Sample size means for a one-sided design with futility bounds

sampleSizeMeans1 <- getSampleSizeMeans(
    getDesignGroupSequential(
        sided = 1,
        futilityBounds = c(0, 0.2)
    )
)

plot(sampleSizeMeans1, type = 1)

Warning: Only the first 'alternative' (0.2) was used for plotting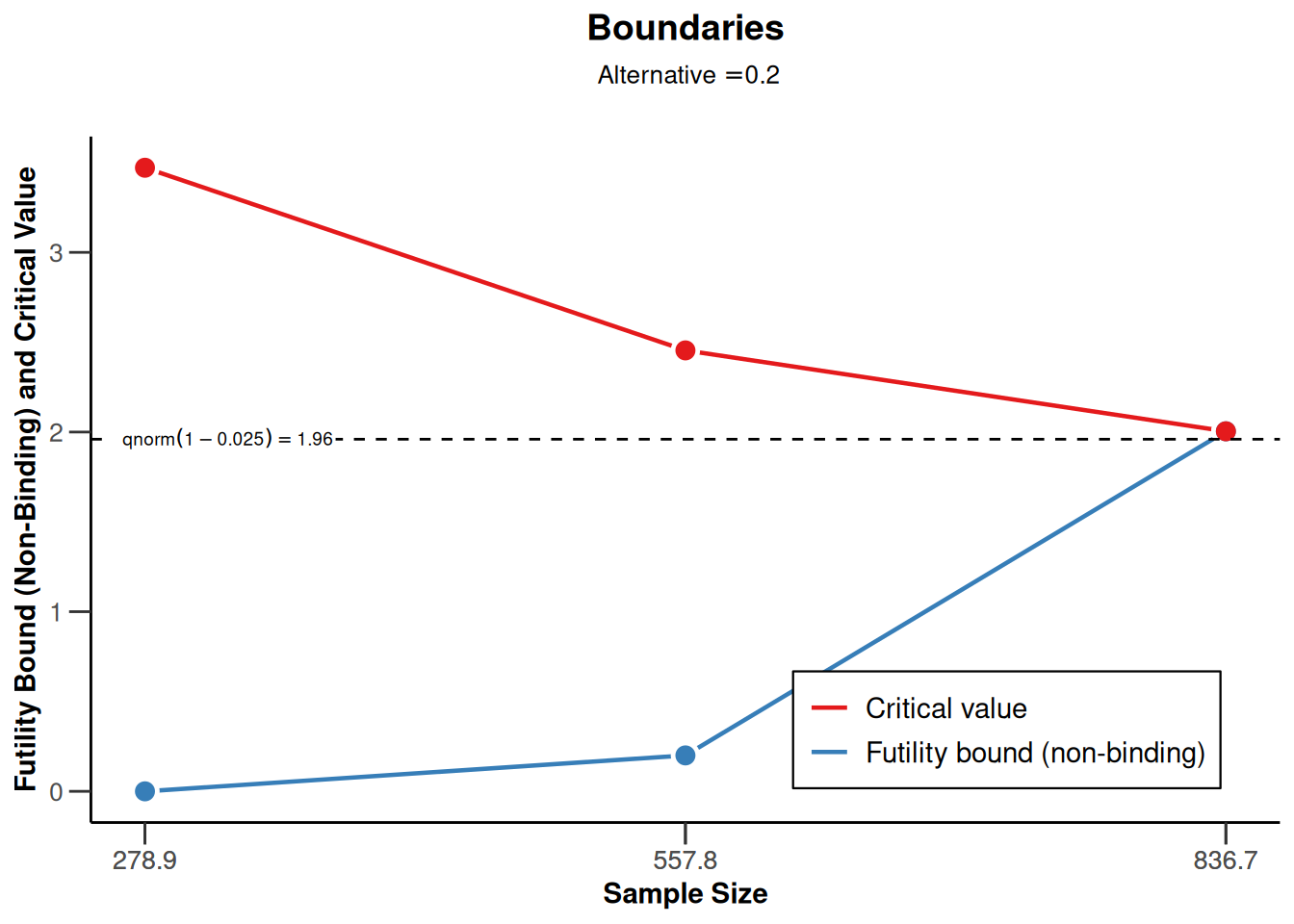

plot(sampleSizeMeans1, type = 2)

Warning: Only the first 'alternative' (0.2) was used for plotting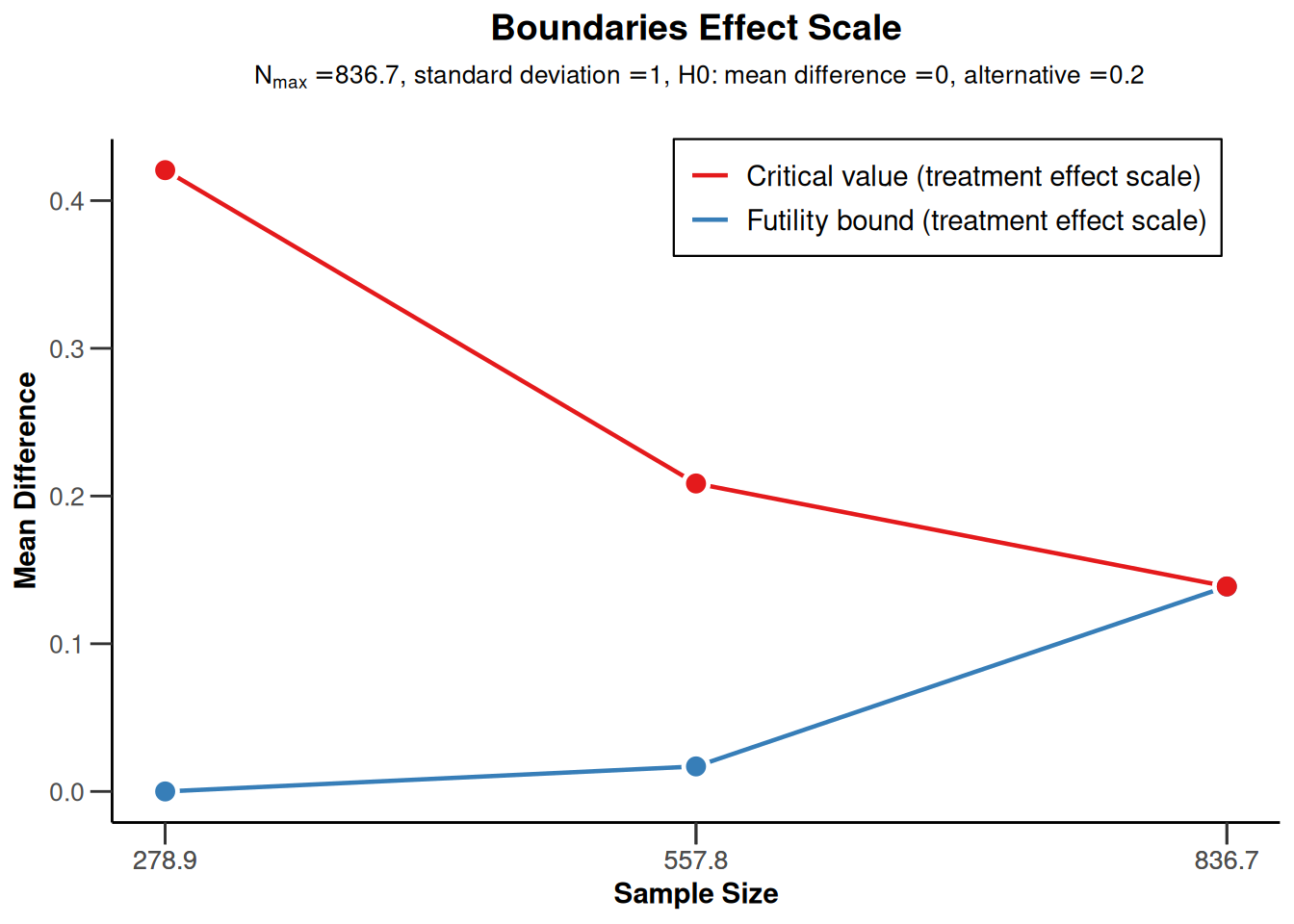

Sample size means for a two-sided design

sampleSizeMeans2 <- getSampleSizeMeans(
    getDesignGroupSequential(sided = 2)
)

plot(sampleSizeMeans2, type = 1)

Warning: Only the first 'alternative' (0.2) was used for plotting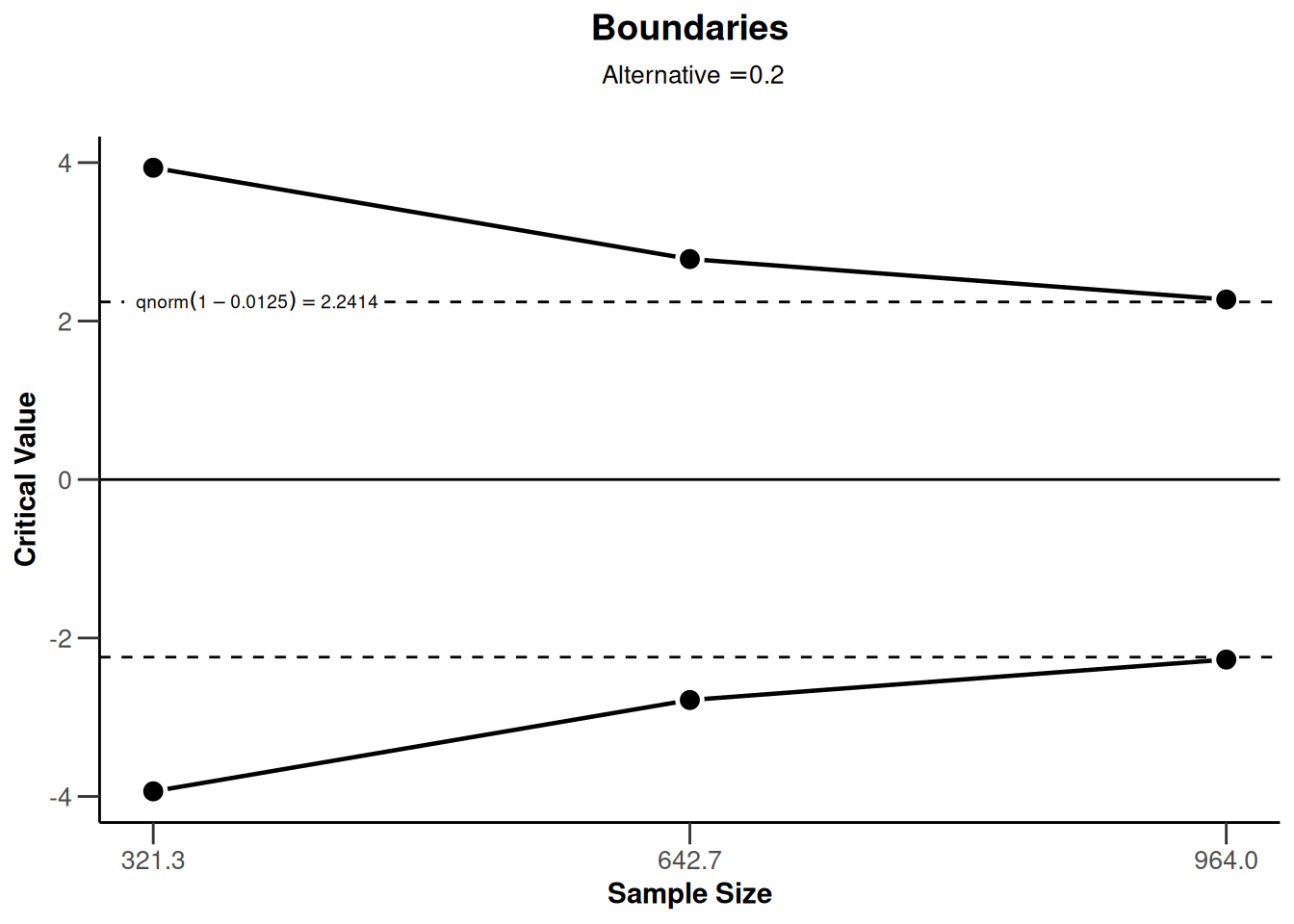

plot(sampleSizeMeans2, type = 2)

Warning: Only the first 'alternative' (0.2) was used for plotting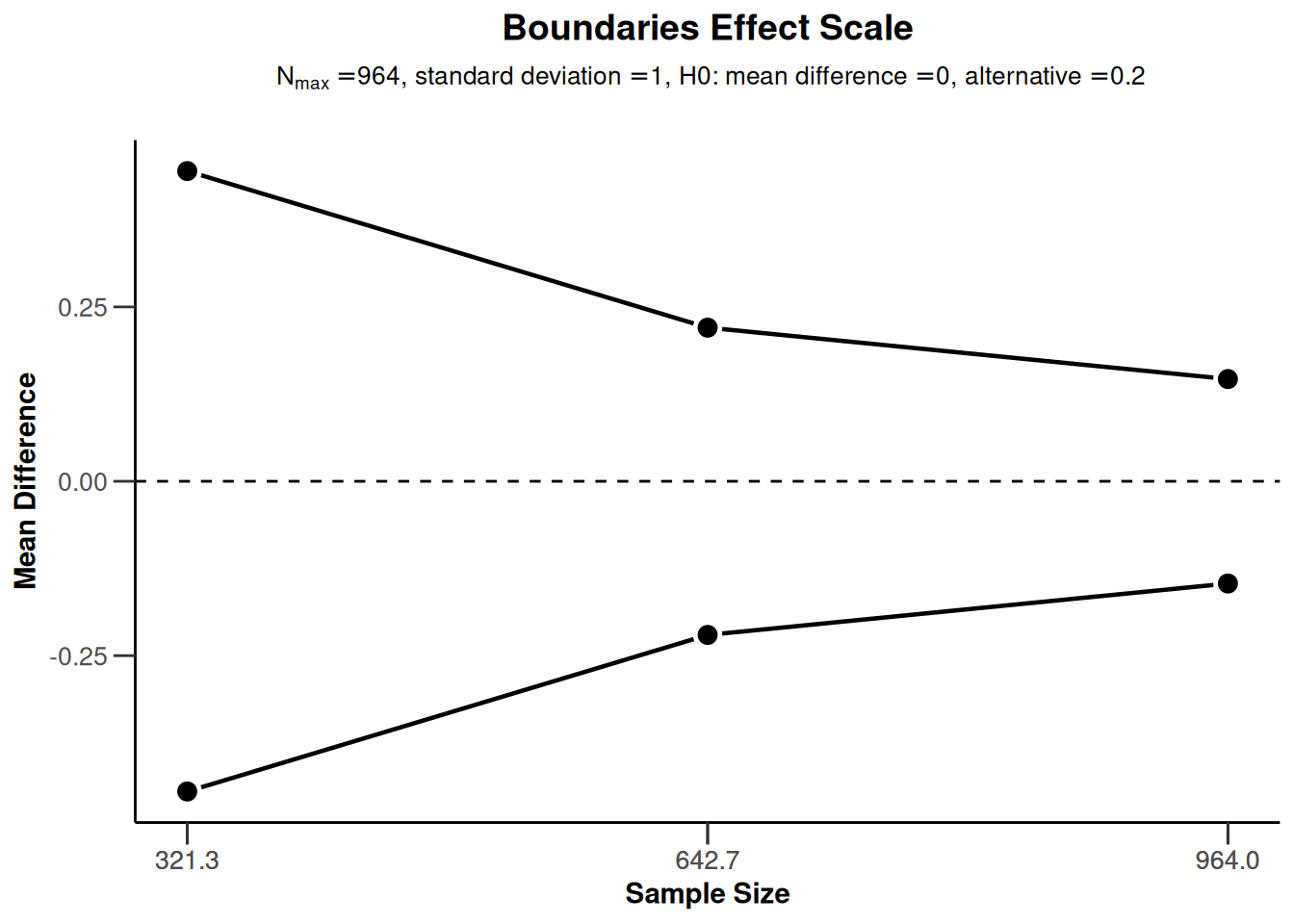

Sample size rates (binary endpoint)

Sample size rates for a one-sided design with futility bounds

sampleSizeRates1 <- getSampleSizeRates(
    getDesignGroupSequential(
        sided = 1,
        futilityBounds = c(0, 0.1)
    )
)

plot(sampleSizeRates1, type = 1)

Warning: Only the first 'pi1' (0.4) was used for plotting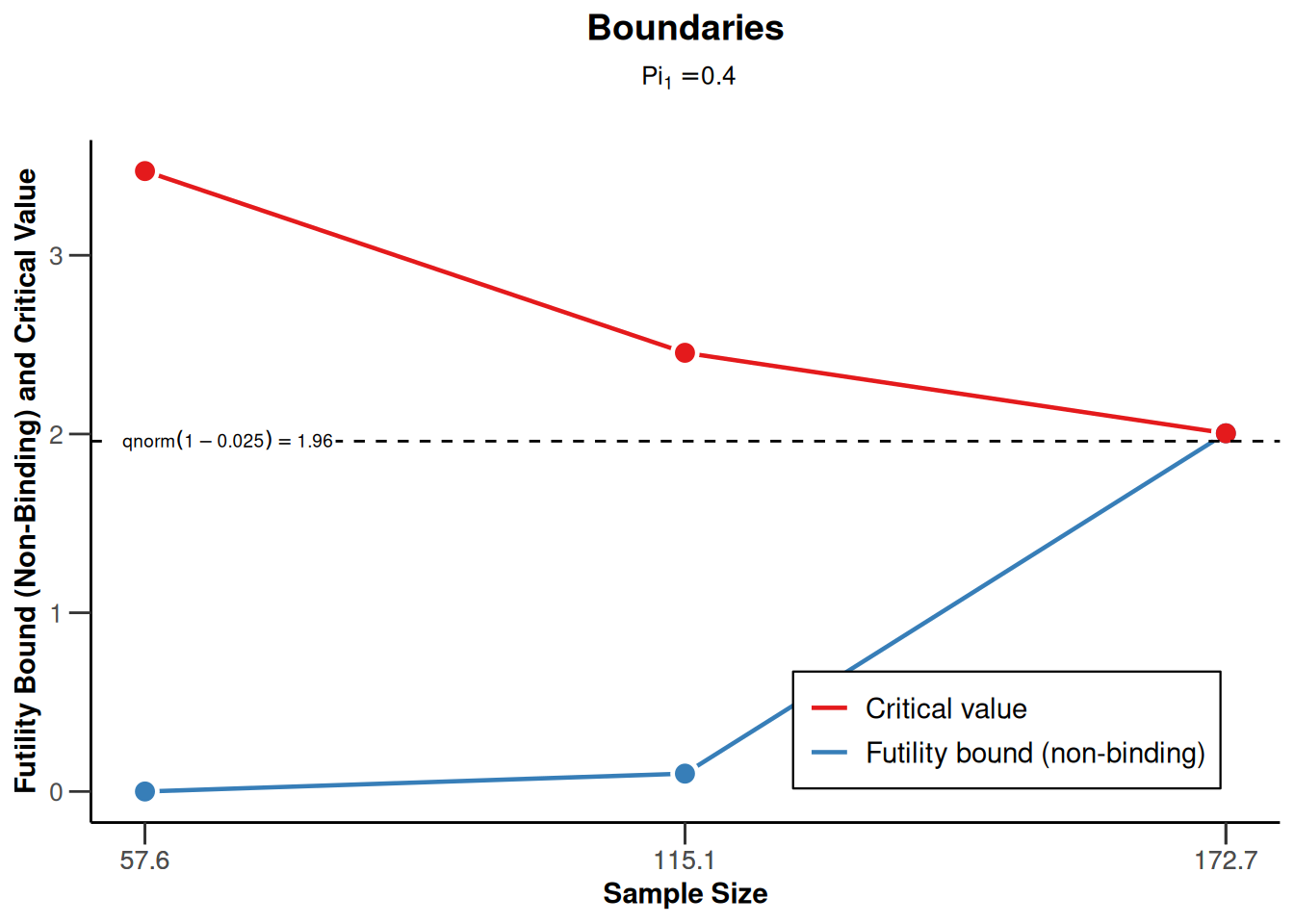

plot(sampleSizeRates1, type = 2)

Warning: Only the first 'pi1' (0.4) was used for plotting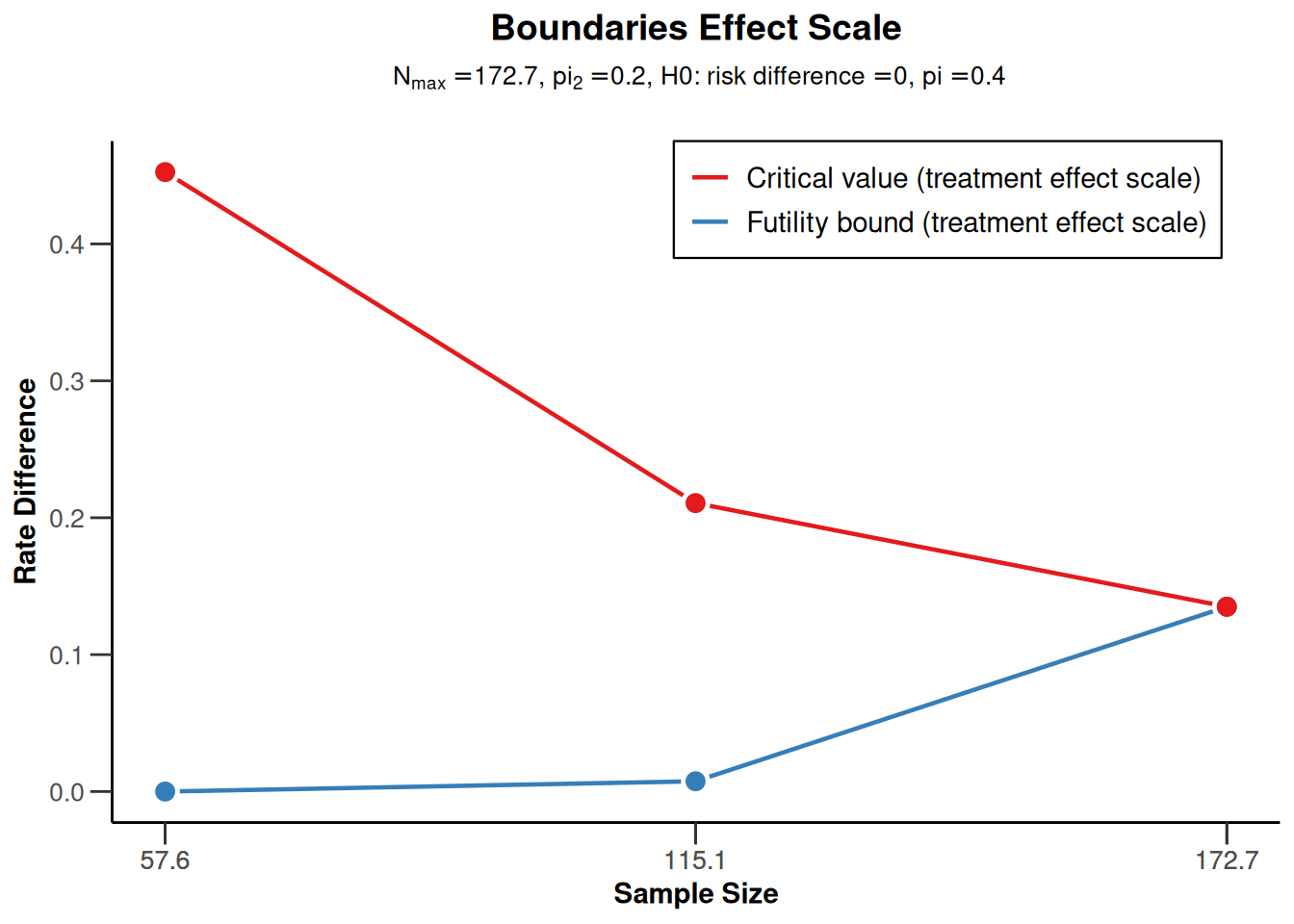

Sample size rates for a two-sided design

sampleSizeRates2 <- getSampleSizeRates(
    getDesignGroupSequential(sided = 2)
)

plot(sampleSizeRates2, type = 1)

Warning: Only the first 'pi1' (0.4) was used for plotting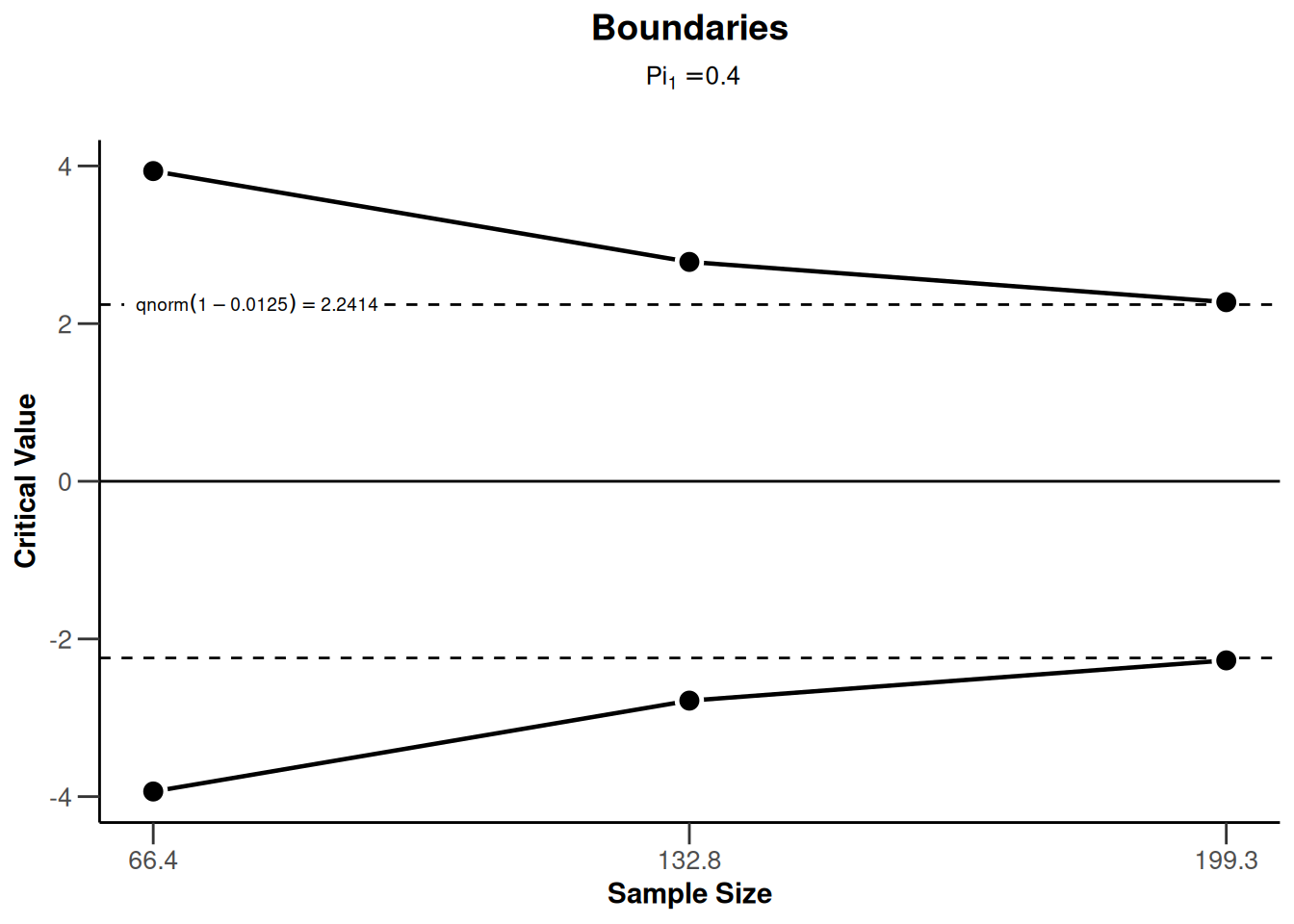

plot(sampleSizeRates2, type = 2)

Warning: Only the first 'pi1' (0.4) was used for plotting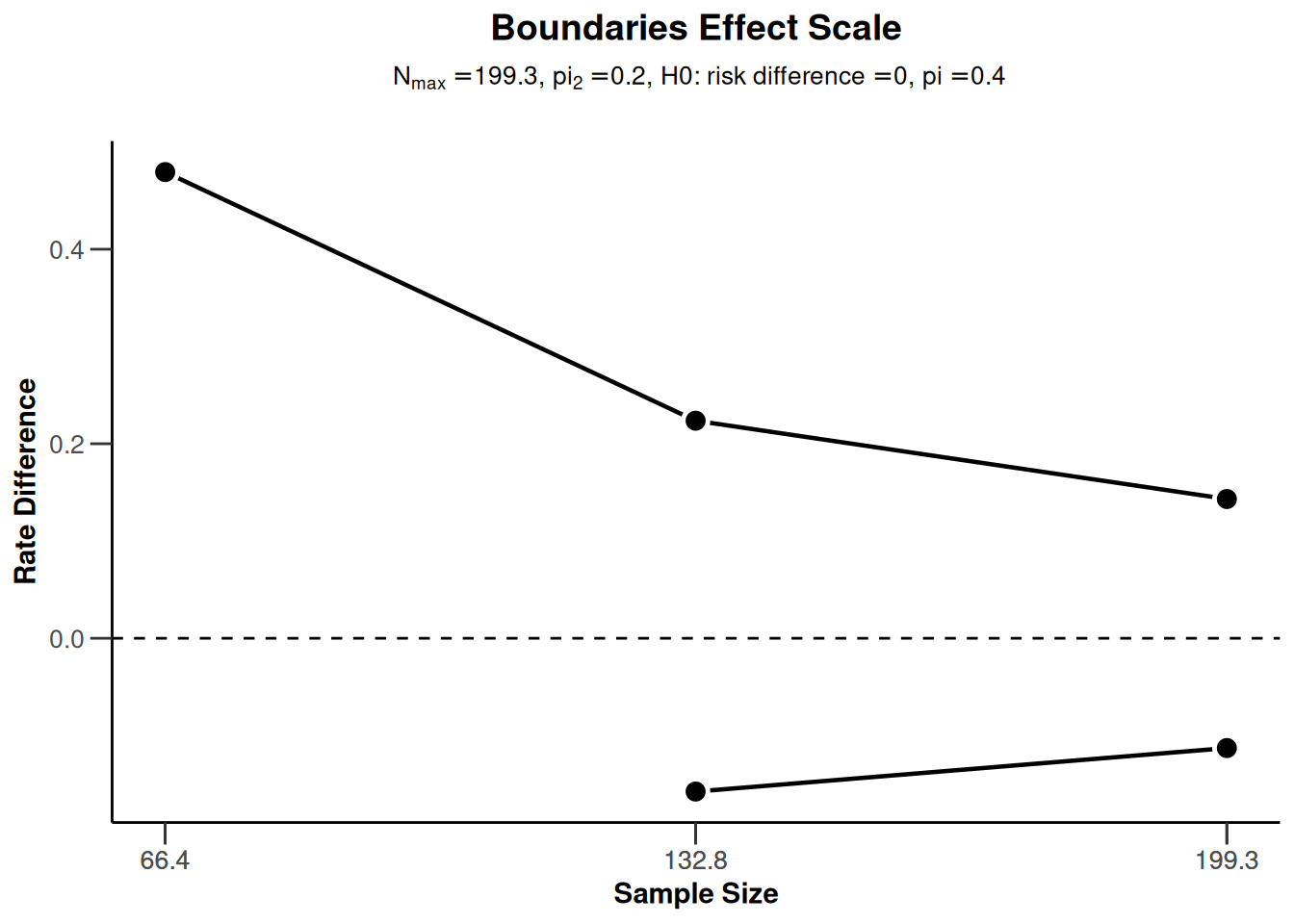

Sample size survival (survival endpoint)

Sample size survival for a one-sided design with futility bounds

design <- getDesignGroupSequential(
    kMax = 3, typeOfDesign = "OF", sided = 1,
    futilityBounds = c(-1, 0.5)
)

piecewiseSurvivalTime <- list(
    "0 - <6" = 0.025,
    "6 - <9" = 0.04,
    "9 - <15" = 0.015,
    "15 - <21" = 0.01,
    ">= 21" = 0.007
)

sampleSizeSurvival1 <- getSampleSizeSurvival(
    design = design,
    typeOfComputation = "Schoenfeld",
    thetaH0 = 1, allocationRatioPlanned = 1, kappa = 1,
    piecewiseSurvivalTime = piecewiseSurvivalTime,
    hazardRatio = c(0.5, 0.9)
)

plot(sampleSizeSurvival1, type = 1)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting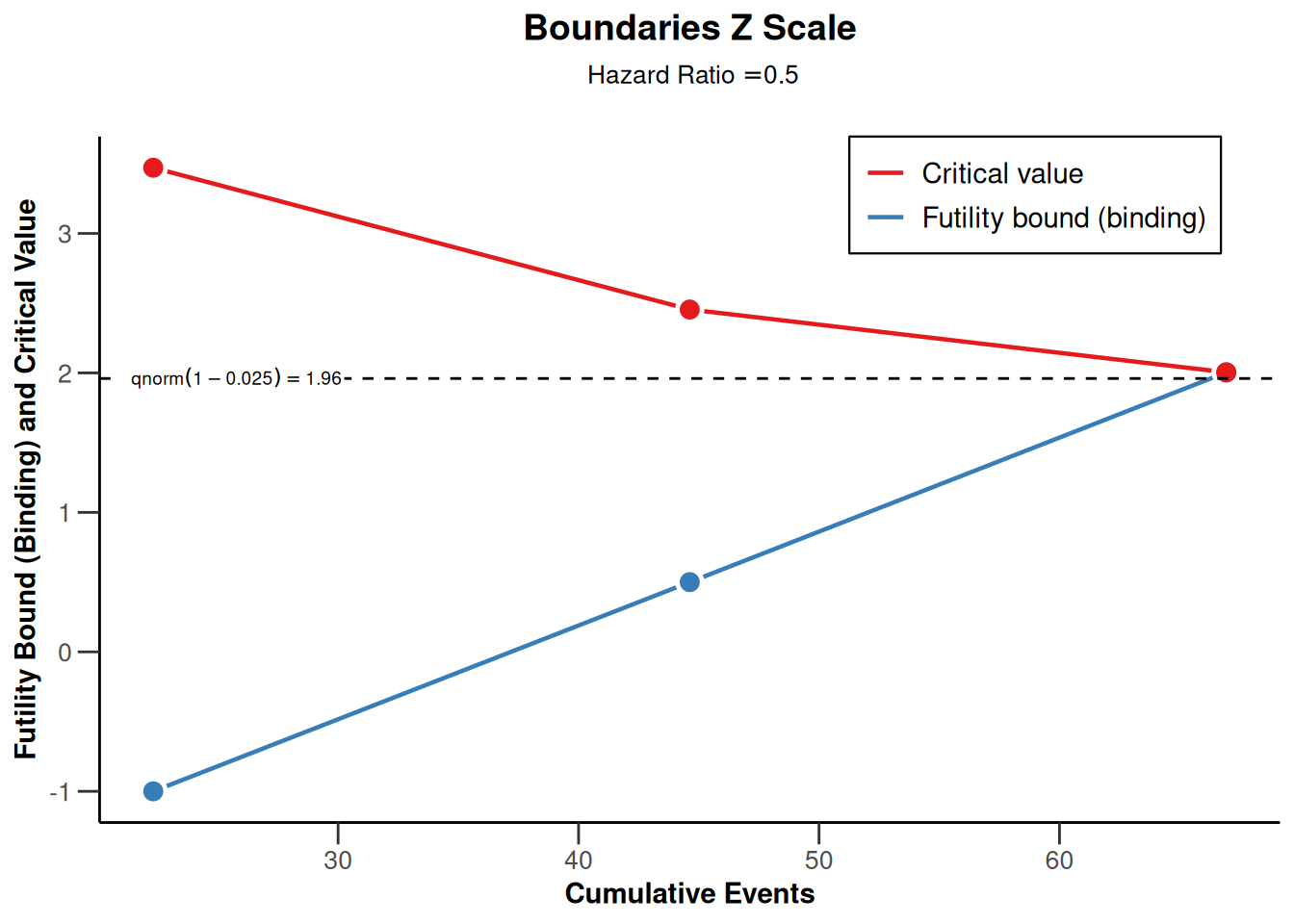

plot(sampleSizeSurvival1, type = 2)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting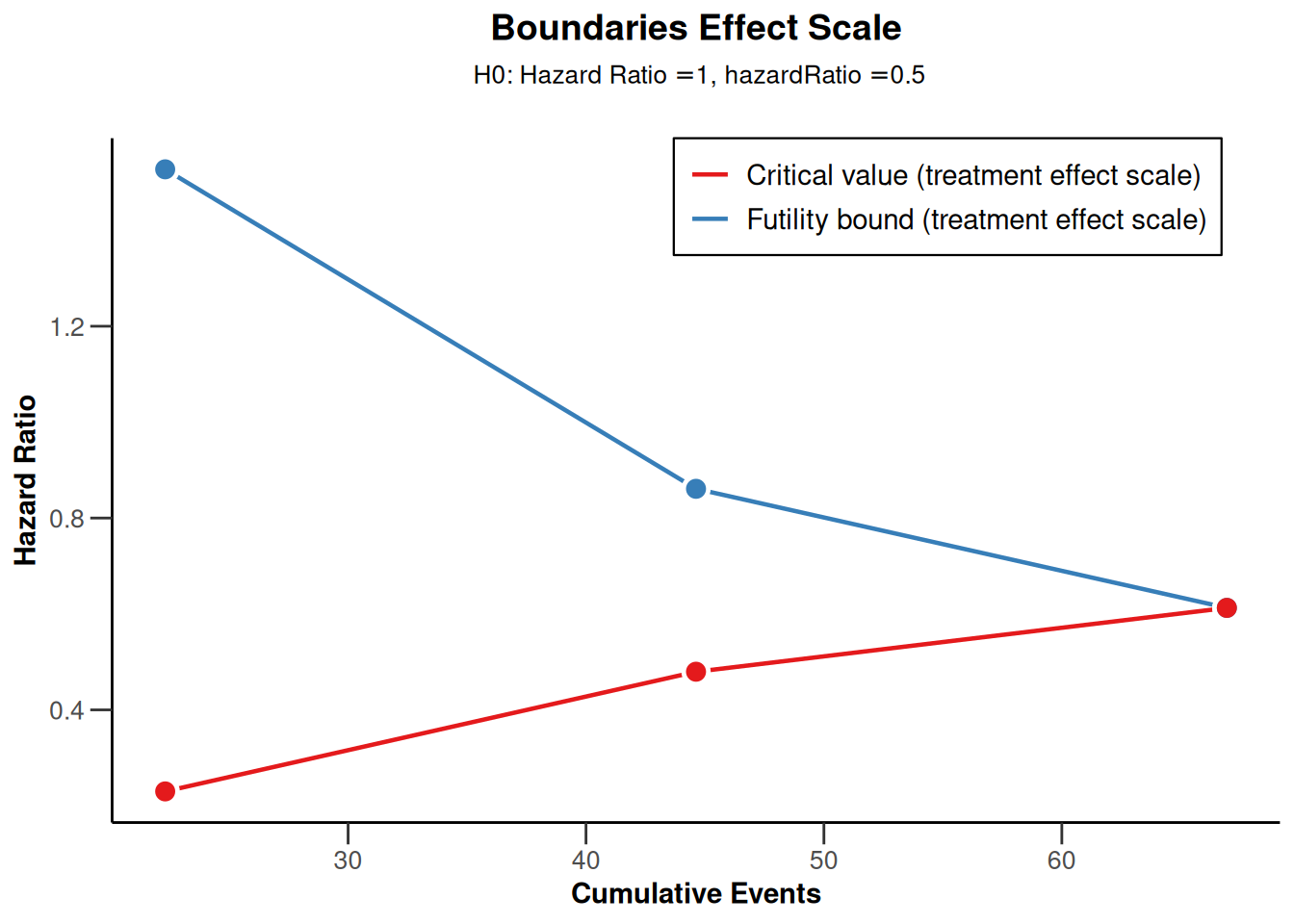

plot(sampleSizeSurvival1, type = 13, legendPosition = 1)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting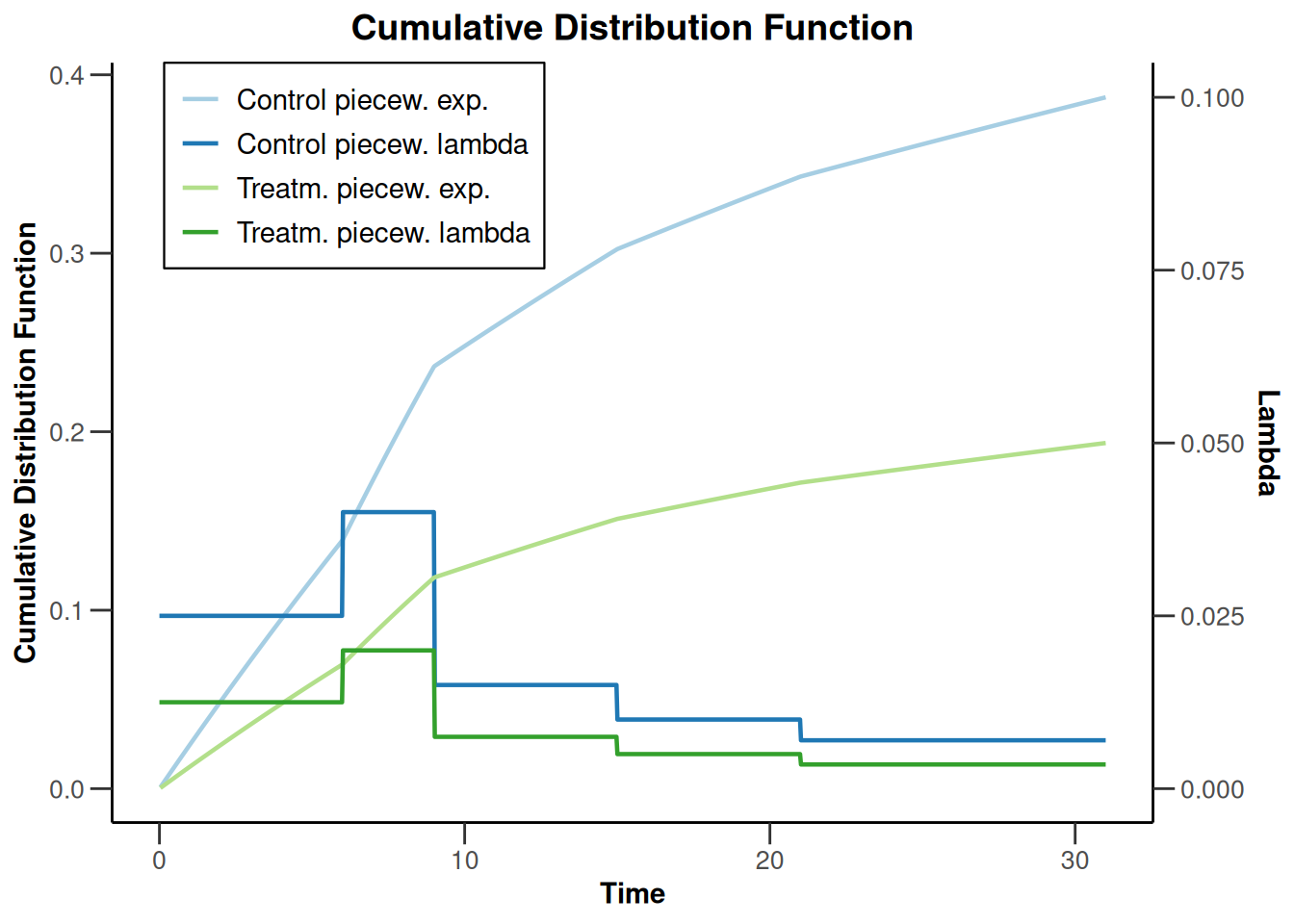

plot(sampleSizeSurvival1, type = 14)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting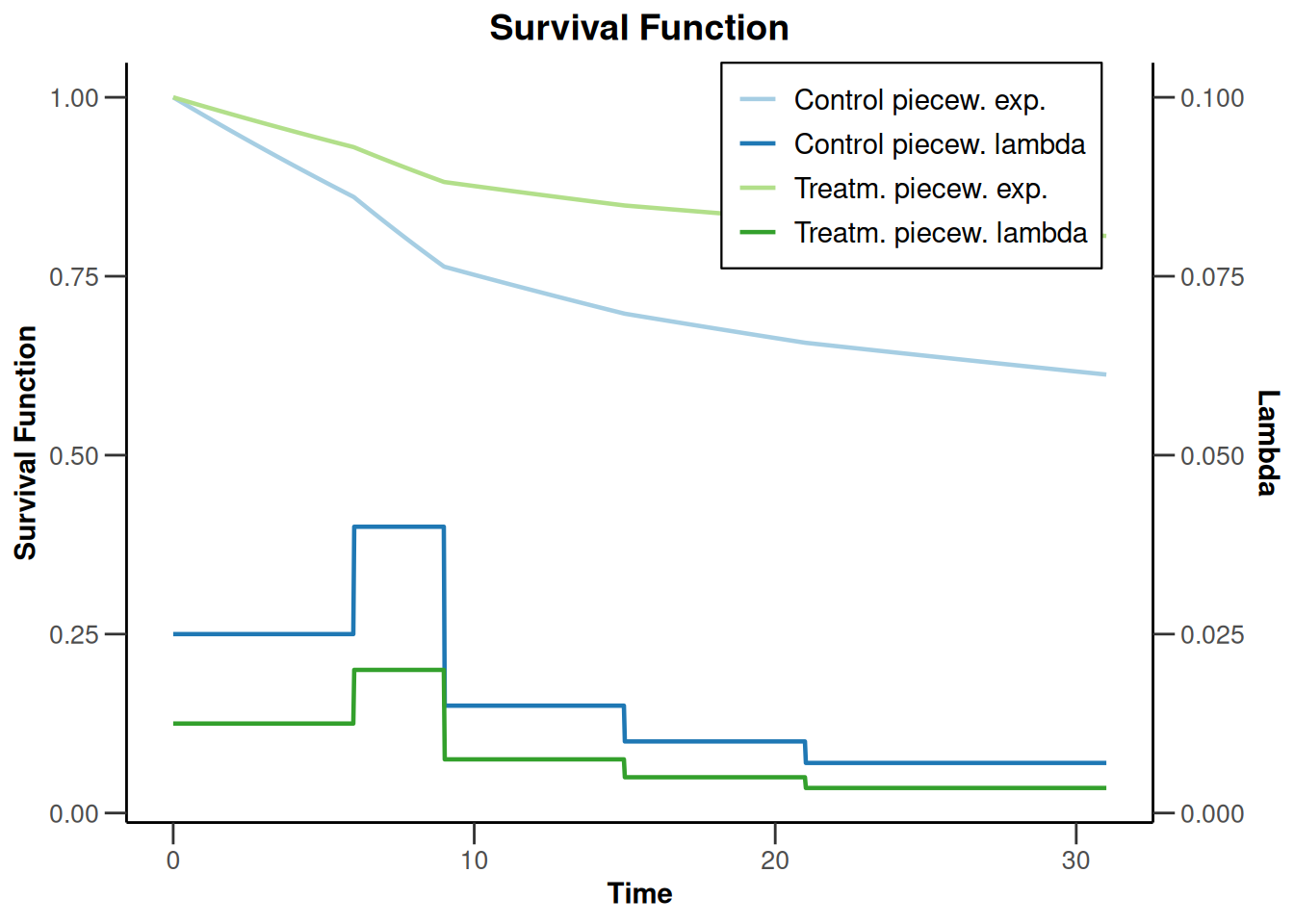

Sample size survival for a two-sided design

design <- getDesignGroupSequential(
    kMax = 3, typeOfDesign = "OF",
    sided = 2, twoSidedPower = TRUE
)

piecewiseSurvivalTime <- list(
    "0  - <14" = 0.015,
    "14 - <24" = 0.01,
    "24 - <44" = 0.005,
    ">= 44" = 0.0025
)
sampleSizeSurvival2 <- getSampleSizeSurvival(
    design = design,
    typeOfComputation = "Schoenfeld",
    thetaH0 = 1,
    allocationRatioPlanned = 1, kappa = 1,
    piecewiseSurvivalTime = piecewiseSurvivalTime,
    maxNumberOfSubjects = 0, hazardRatio = c(0.1, 0.2, 0.5, 0.6)
)

plot(sampleSizeSurvival2, type = 1)

Warning: Only the first 'hazardRatio' (0.1) was used for plotting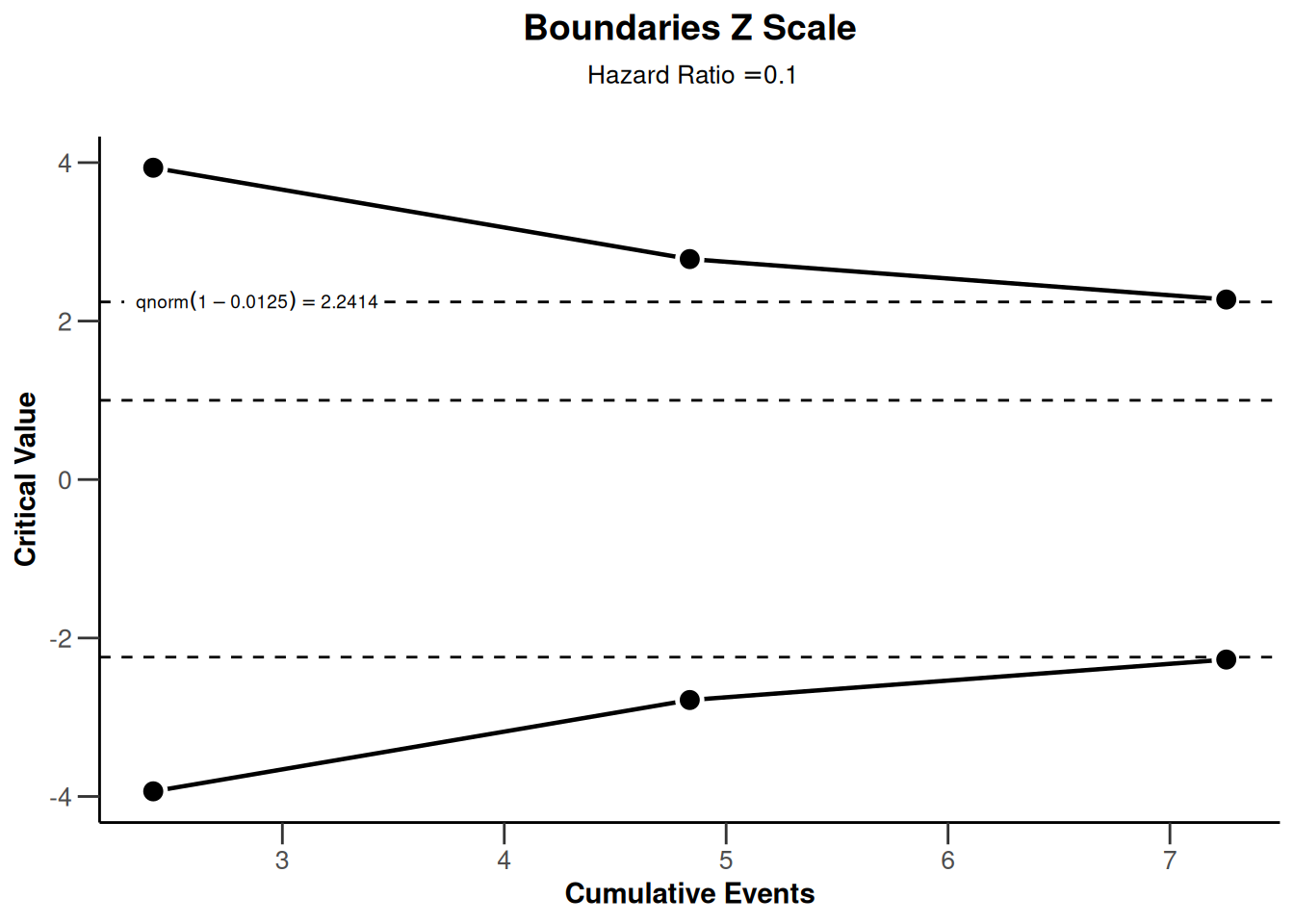

plot(sampleSizeSurvival2, type = 2)

Warning: Only the first 'hazardRatio' (0.1) was used for plotting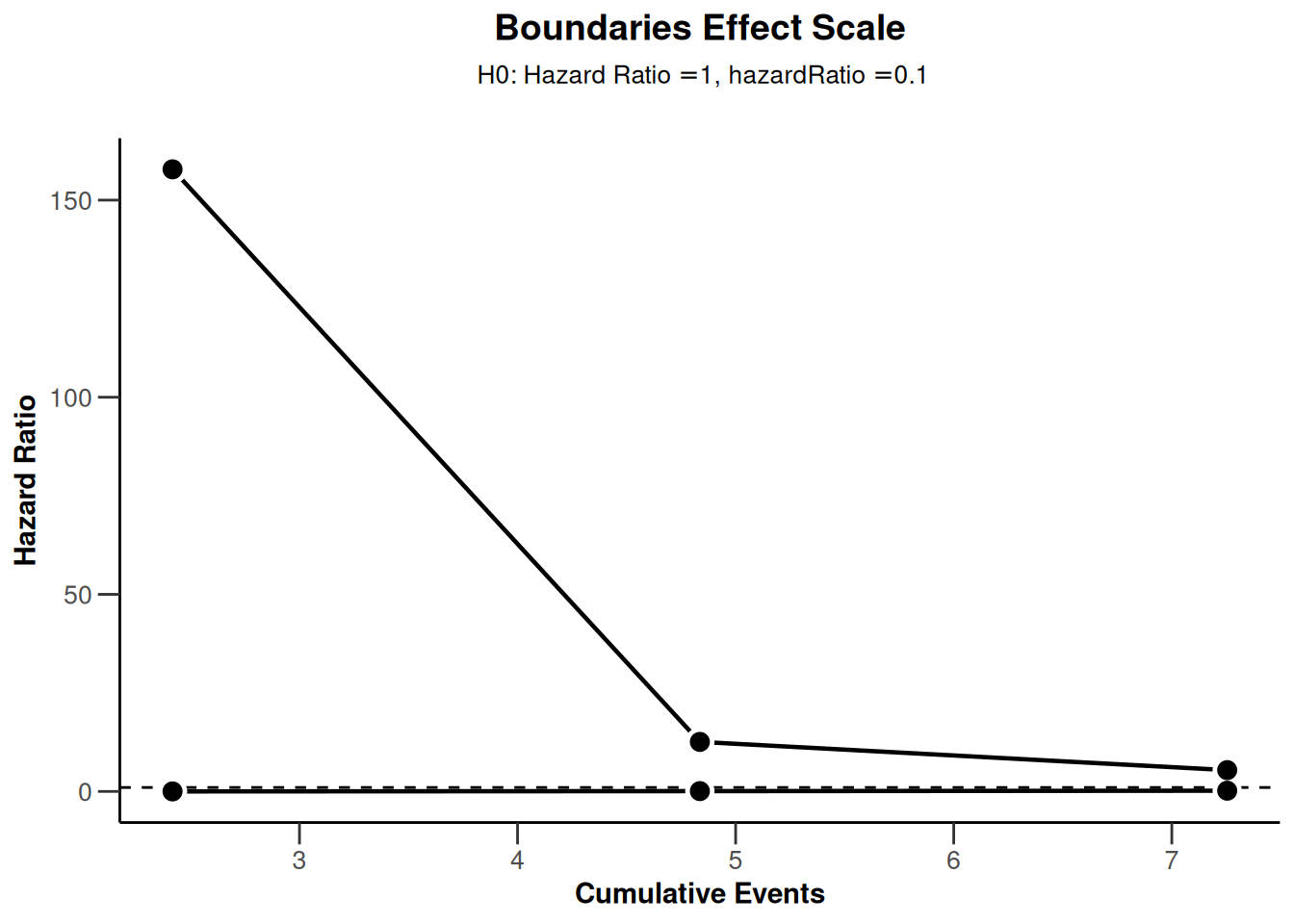

plot(sampleSizeSurvival2, type = 13, legendPosition = 1)

Warning: Only the first 'hazardRatio' (0.1) was used for plotting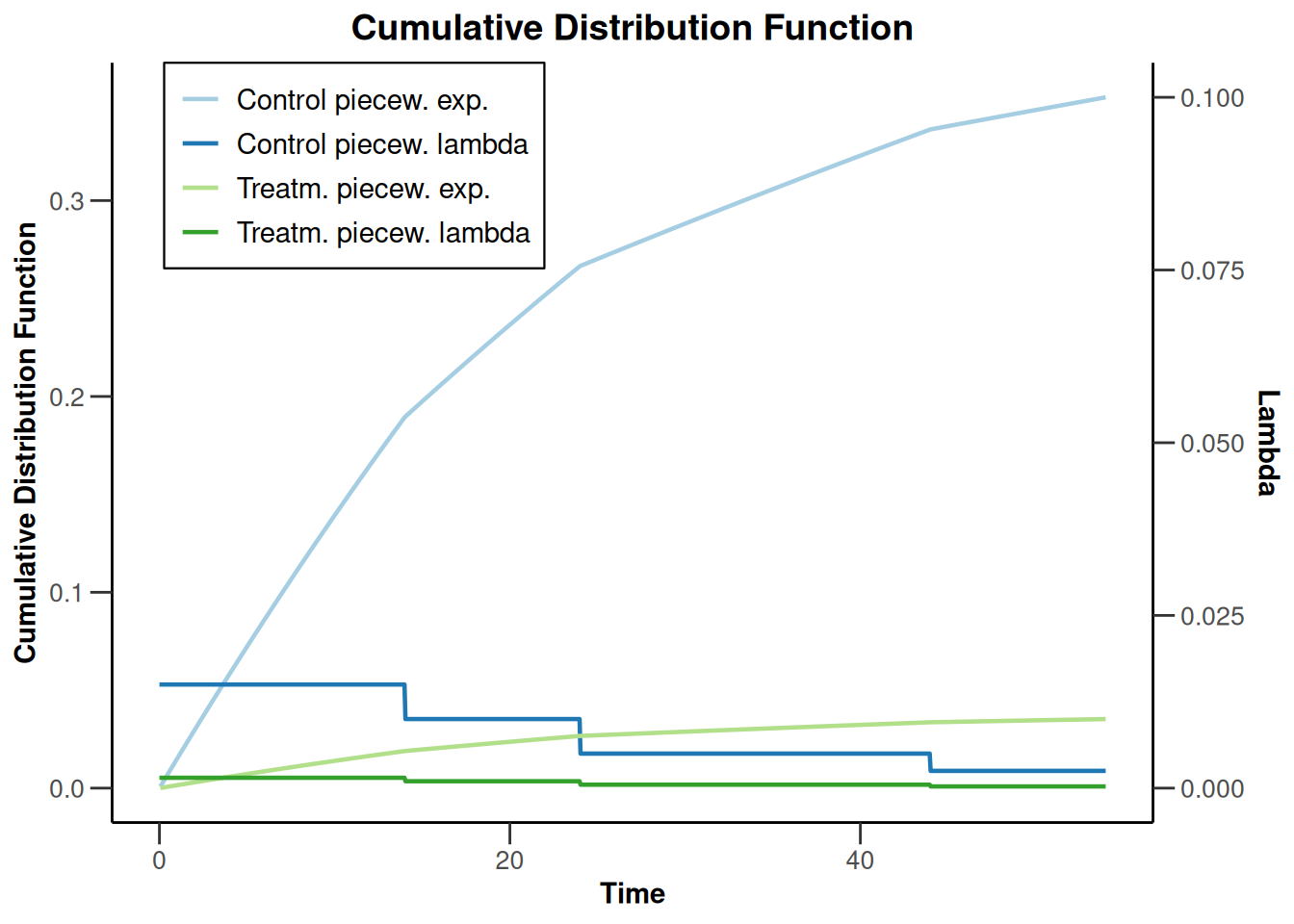

plot(sampleSizeSurvival2, type = 14)

Warning: Only the first 'hazardRatio' (0.1) was used for plotting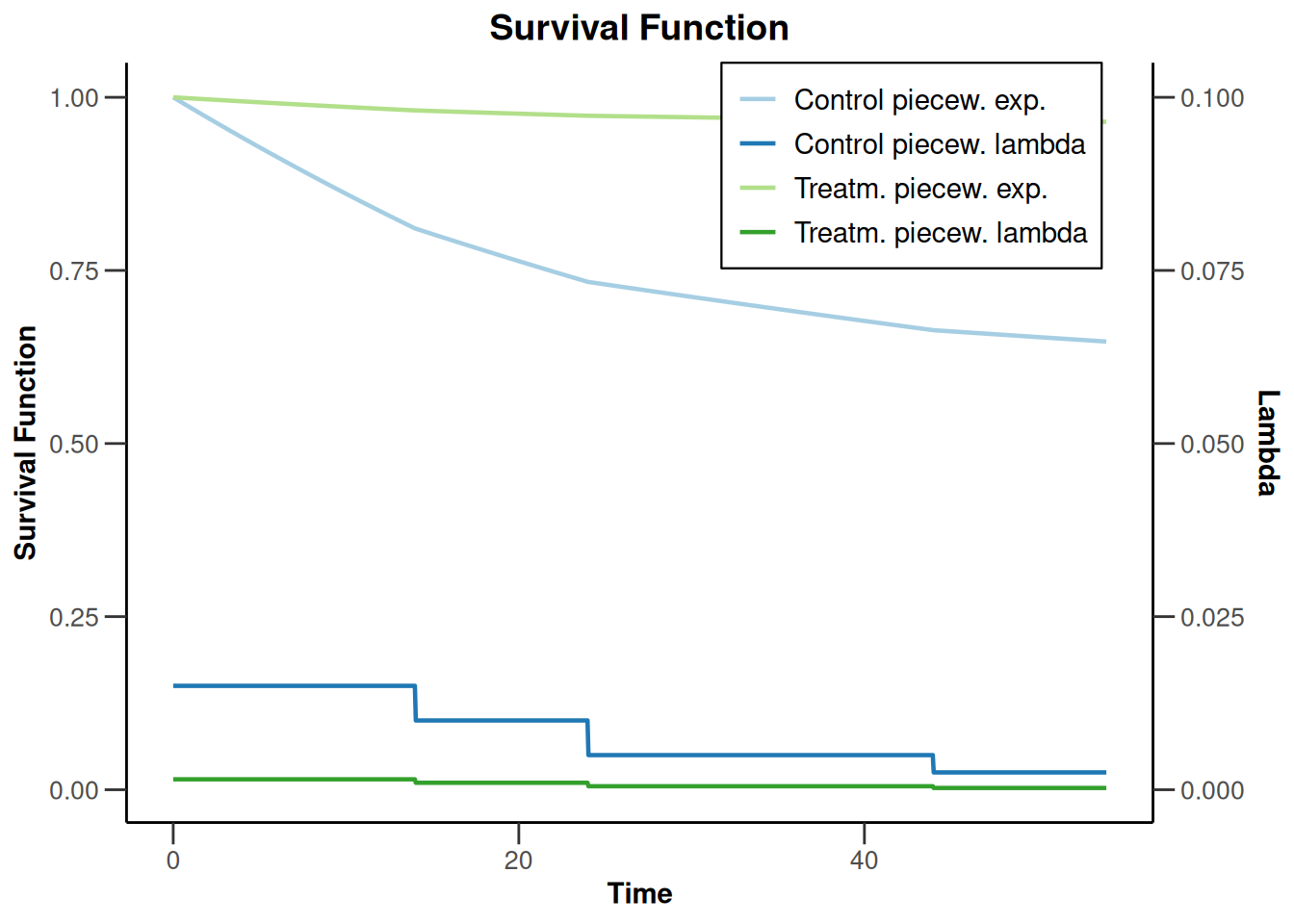

Power plots

Power means (continuous endpoint)

Power means for a one-sided design with futility bounds

design <- getDesignGroupSequential(
    typeOfDesign = "OF", sided = 1,
    futilityBounds = c(0, 0.5)
)

powerMeans1 <- getPowerMeans(design,
    groups = 1, meanRatio = FALSE,
    thetaH0 = 0, alternative = c(-1, 4),
    stDev = 2, normalApproximation = FALSE,
    maxNumberOfSubjects = 40
)

plot(powerMeans1, type = 1)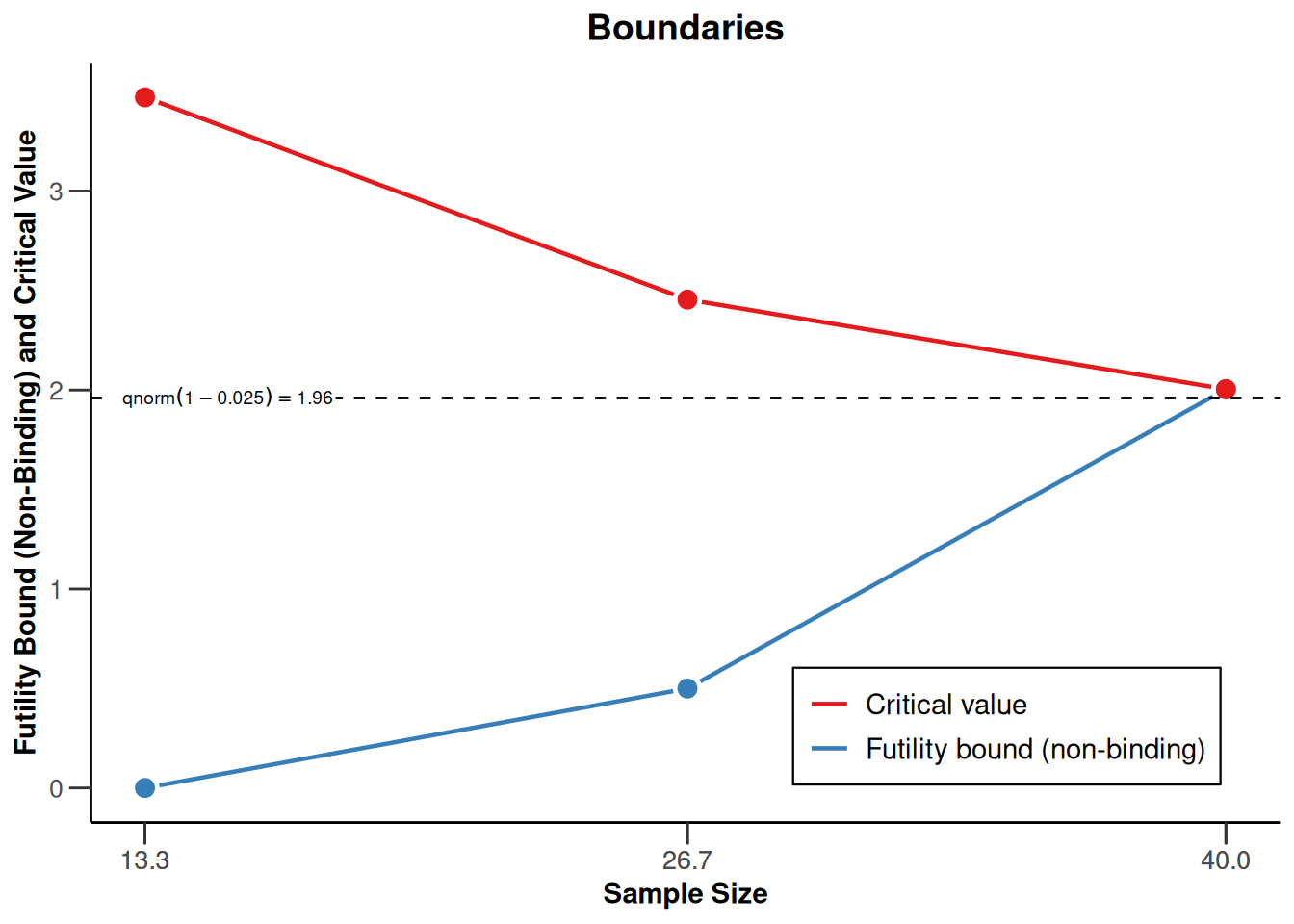

plot(powerMeans1, type = 2)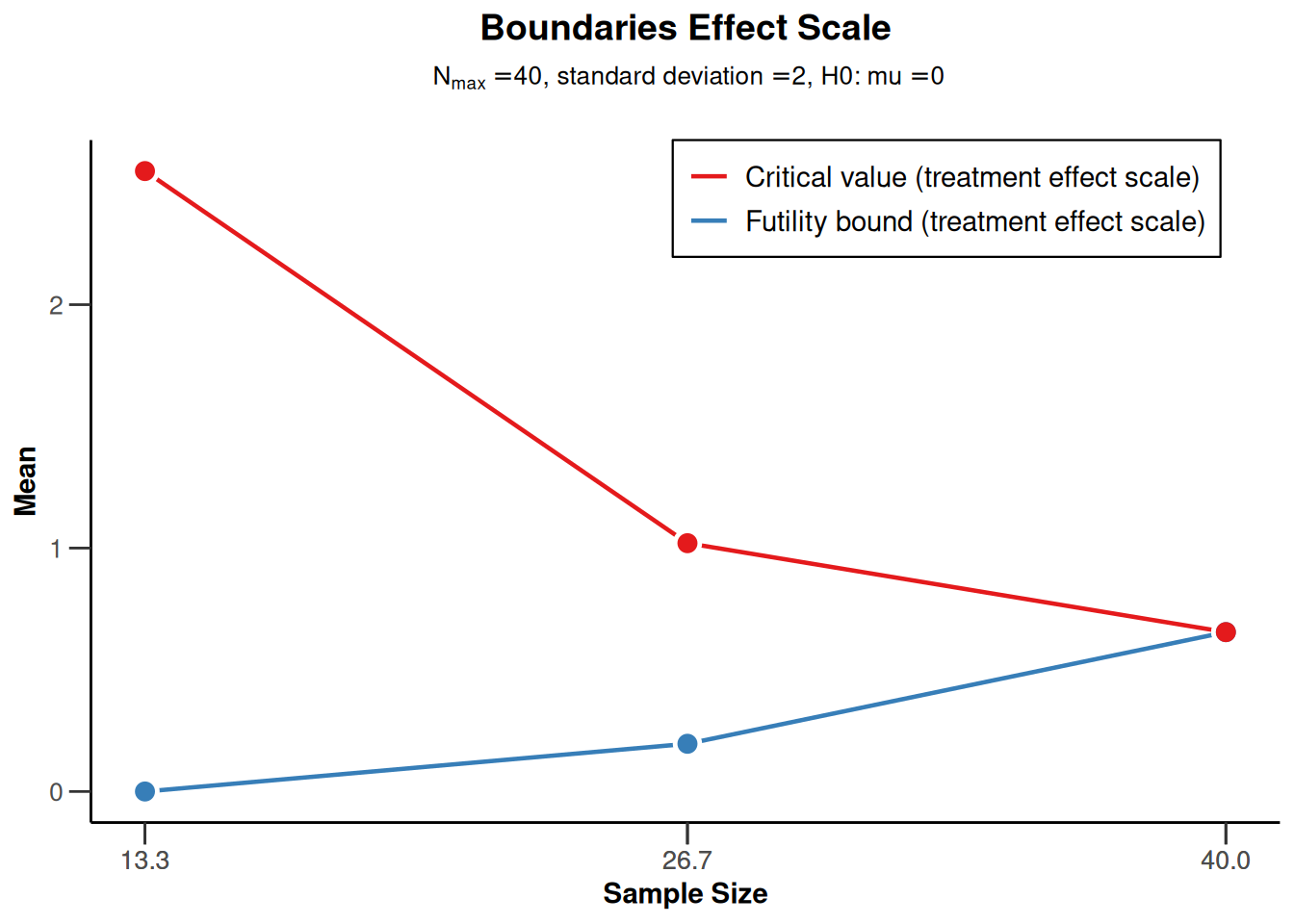

plot(powerMeans1, type = 5)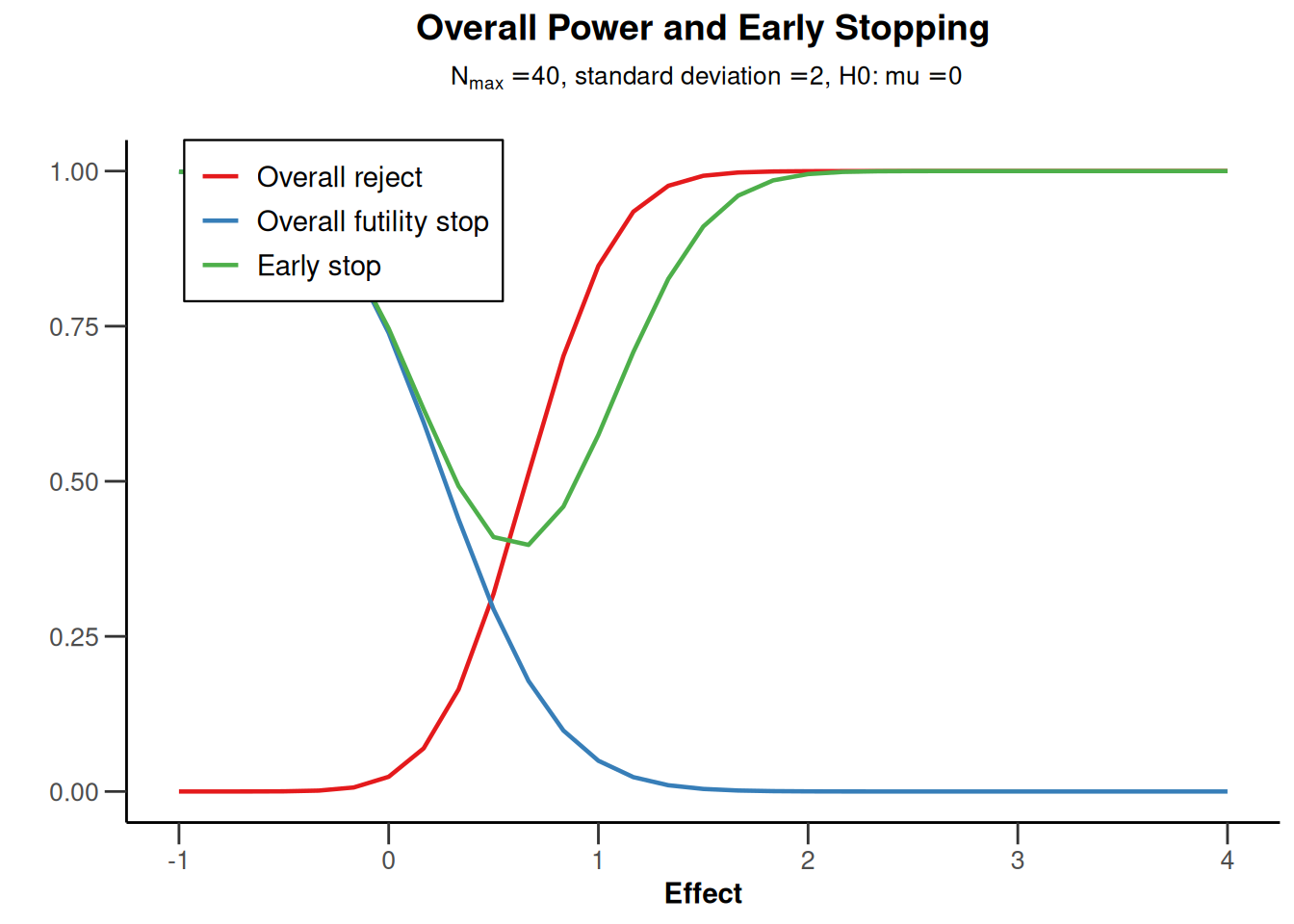

plot(powerMeans1, type = 6)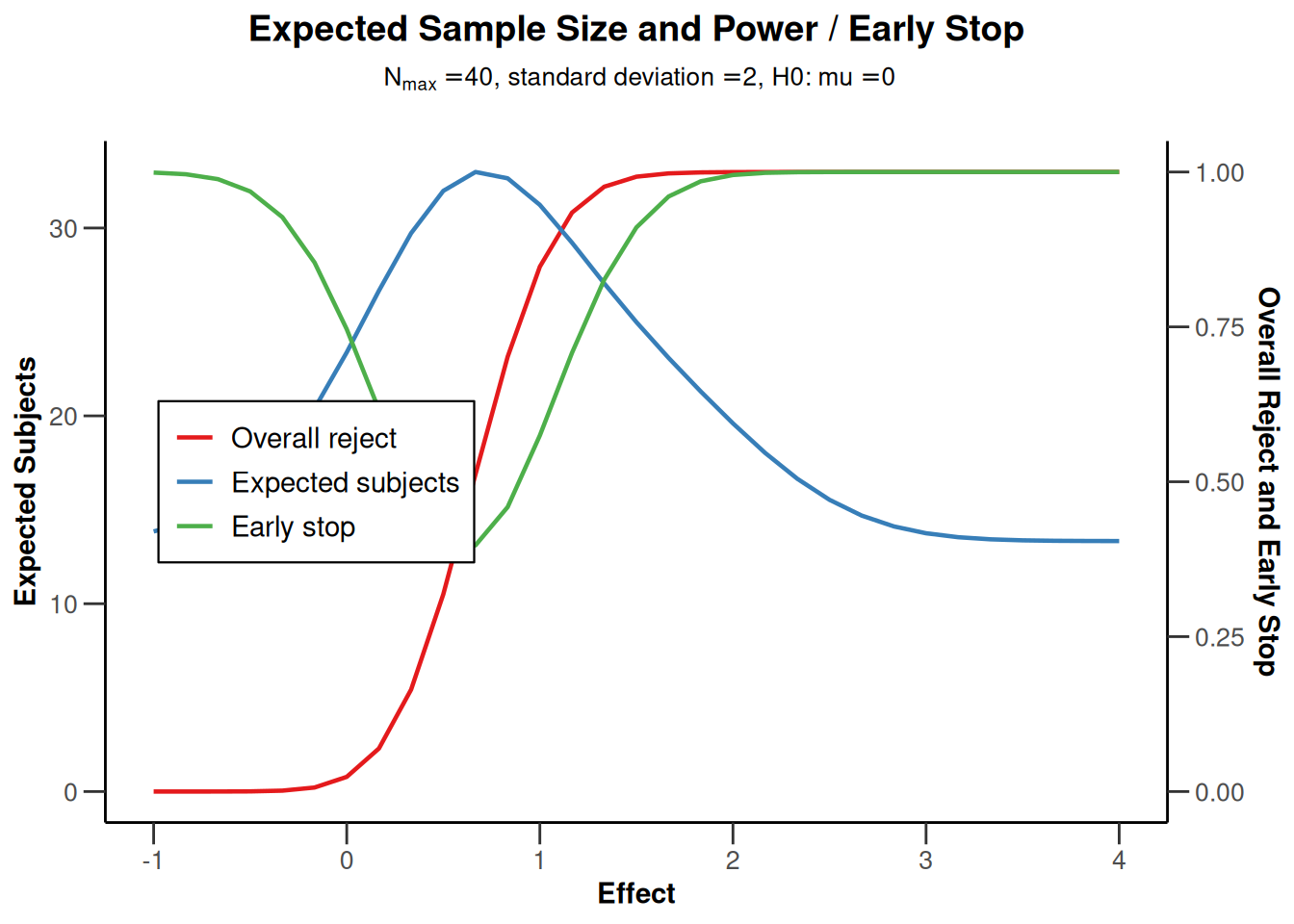

Power means for a two-sided design

powerMeans2 <- getPowerMeans(
    getDesignGroupSequential(
        typeOfDesign = "OF", sided = 2, twoSidedPower = TRUE
    ),
    maxNumberOfSubjects = 30
)

plot(powerMeans2, type = 1)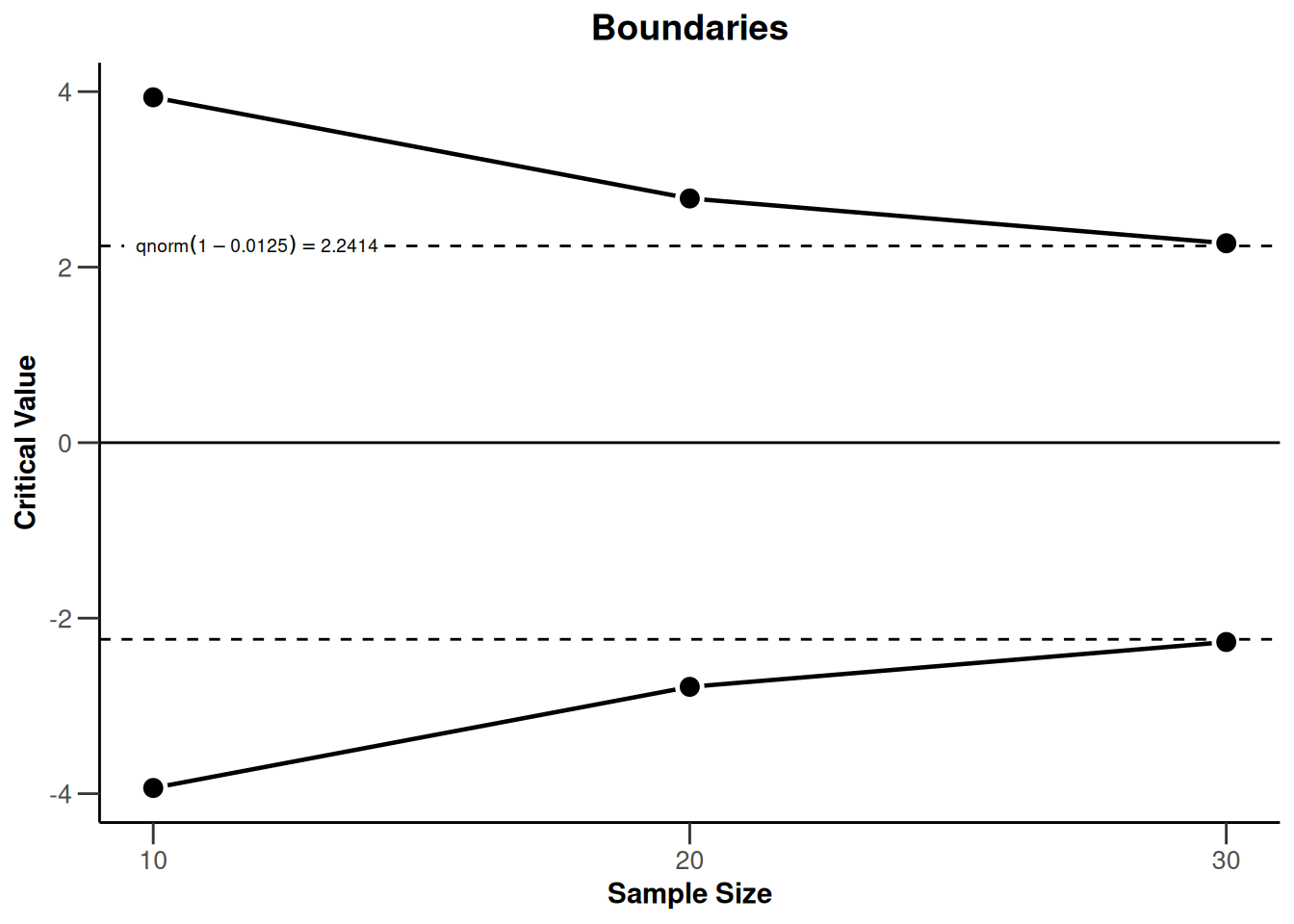

plot(powerMeans2, type = 2)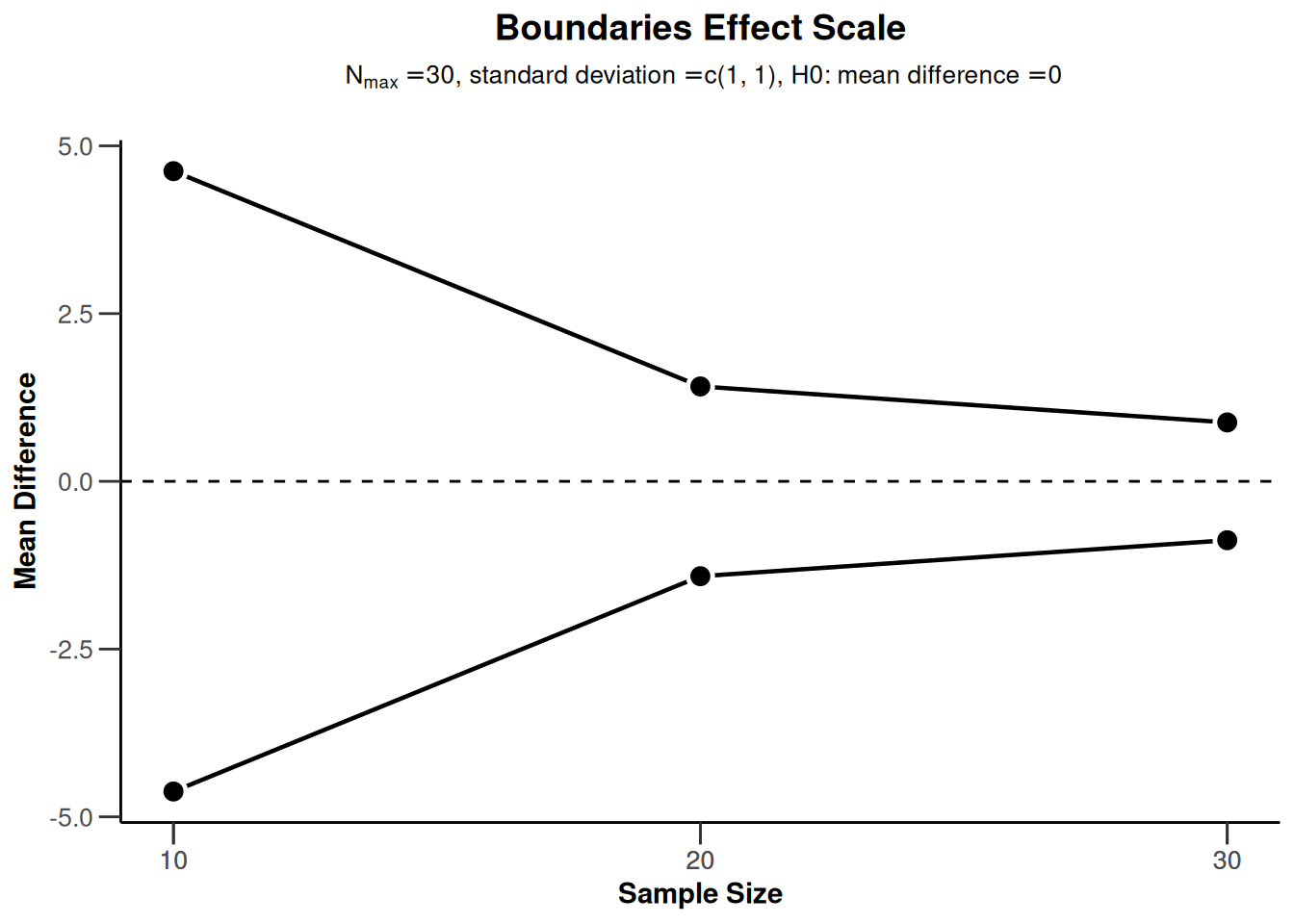

plot(powerMeans2, type = 5)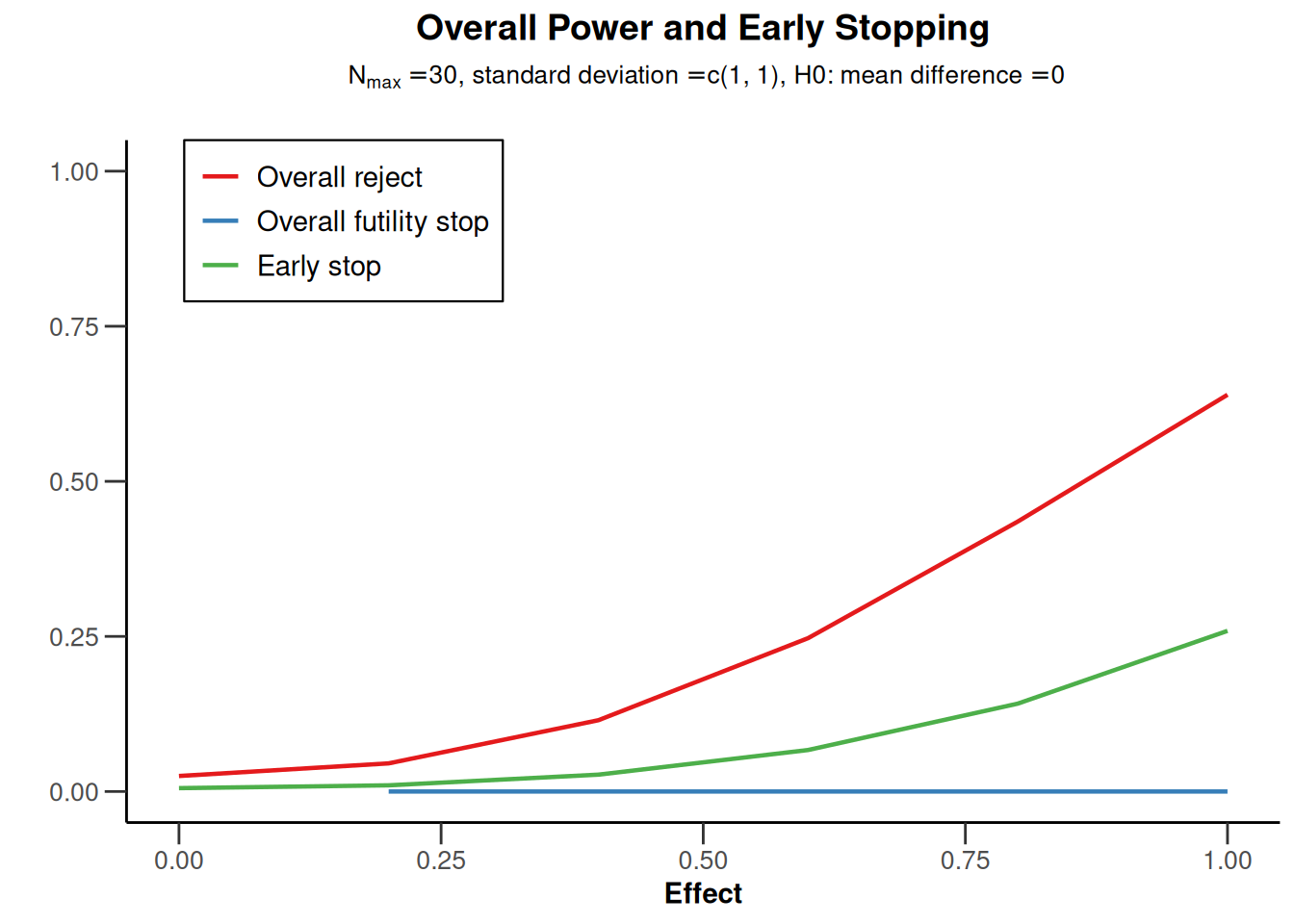

plot(powerMeans2, type = 6)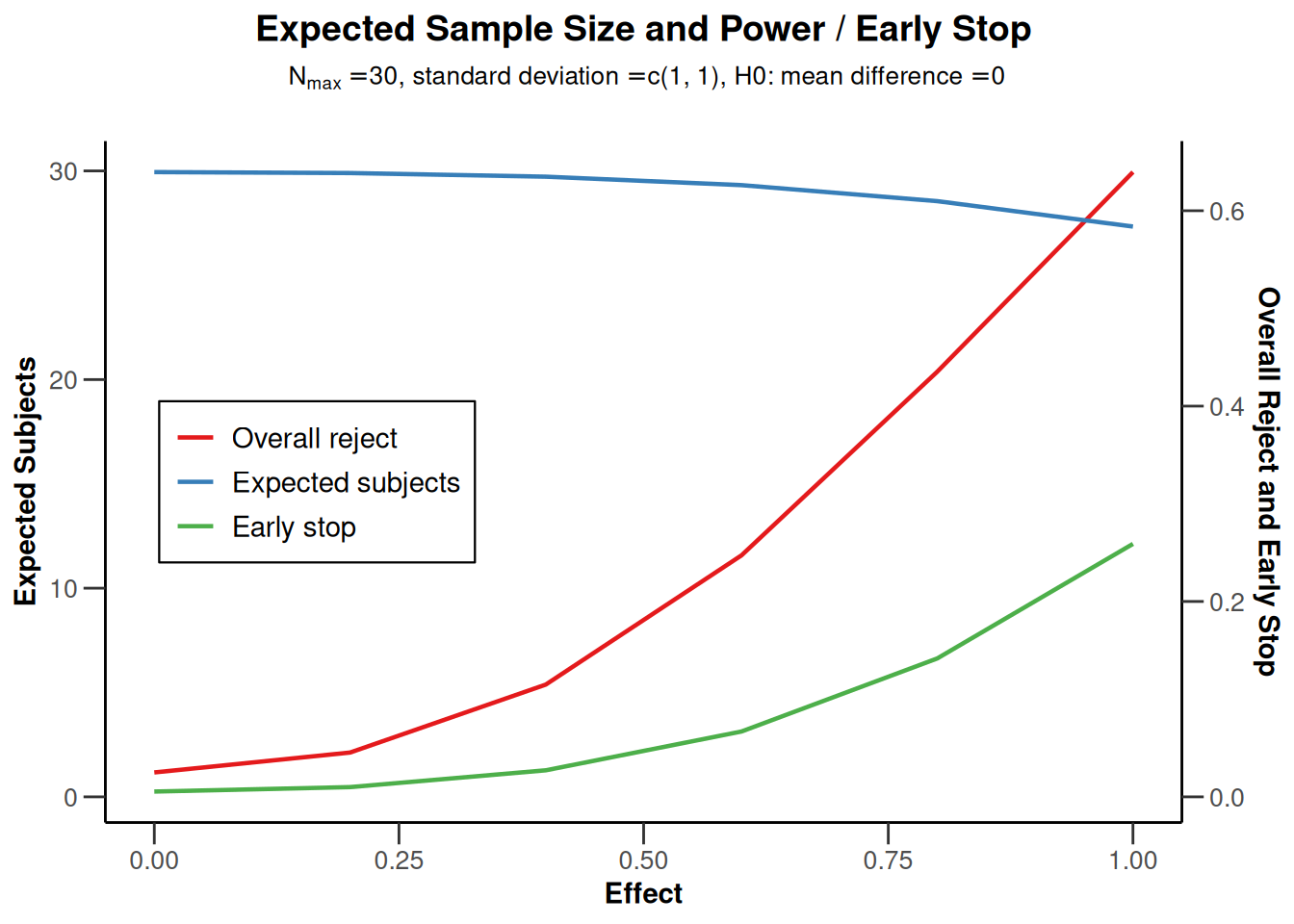

Power rates (binary endpoint)

Power rates for a one-sided design with futility bounds

design <- getDesignGroupSequential(
    kMax = 3,
    typeOfDesign = "OF",
    sided = 1,
    futilityBounds = c(-1, 0.5)
)

powerRates1 <- getPowerRates(design,
    groups = 2, riskRatio = TRUE,
    thetaH0 = 0.2, allocationRatioPlanned = 1,
    pi1 = c(0.1, 0.4), pi2 = 0.2,
    maxNumberOfSubjects = 80
)

plot(powerRates1, type = 1)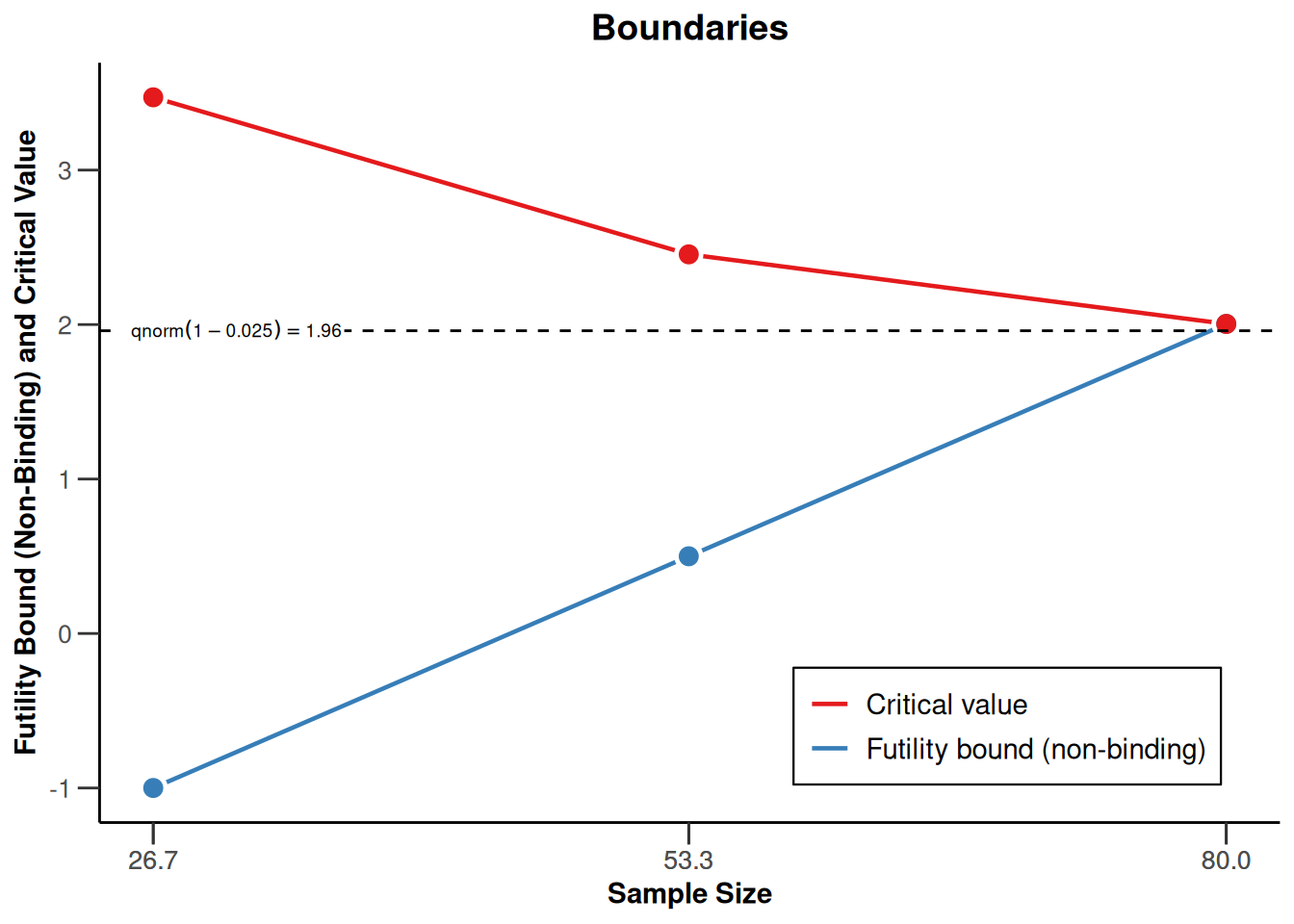

plot(powerRates1, type = 2)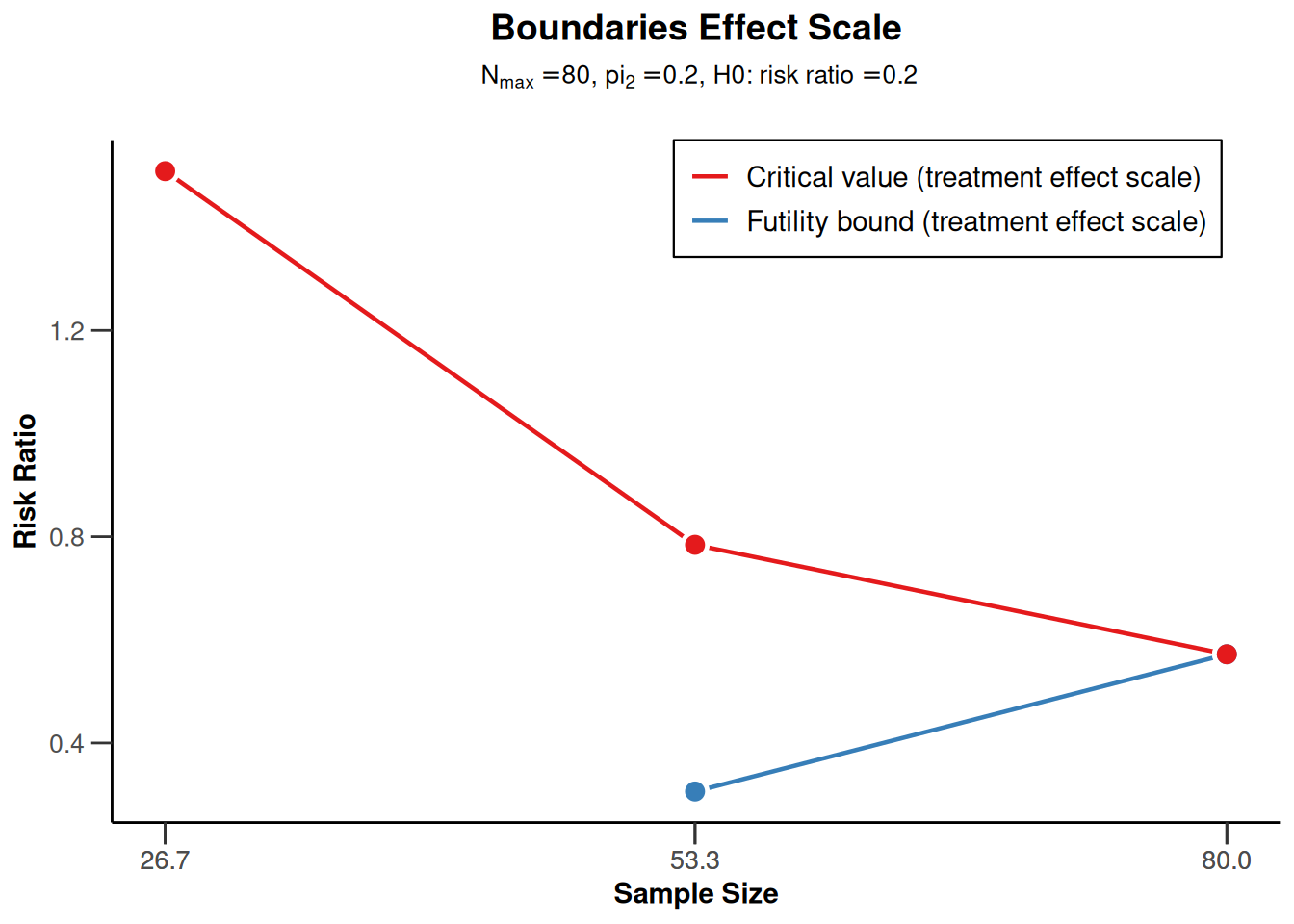

plot(powerRates1, type = 5)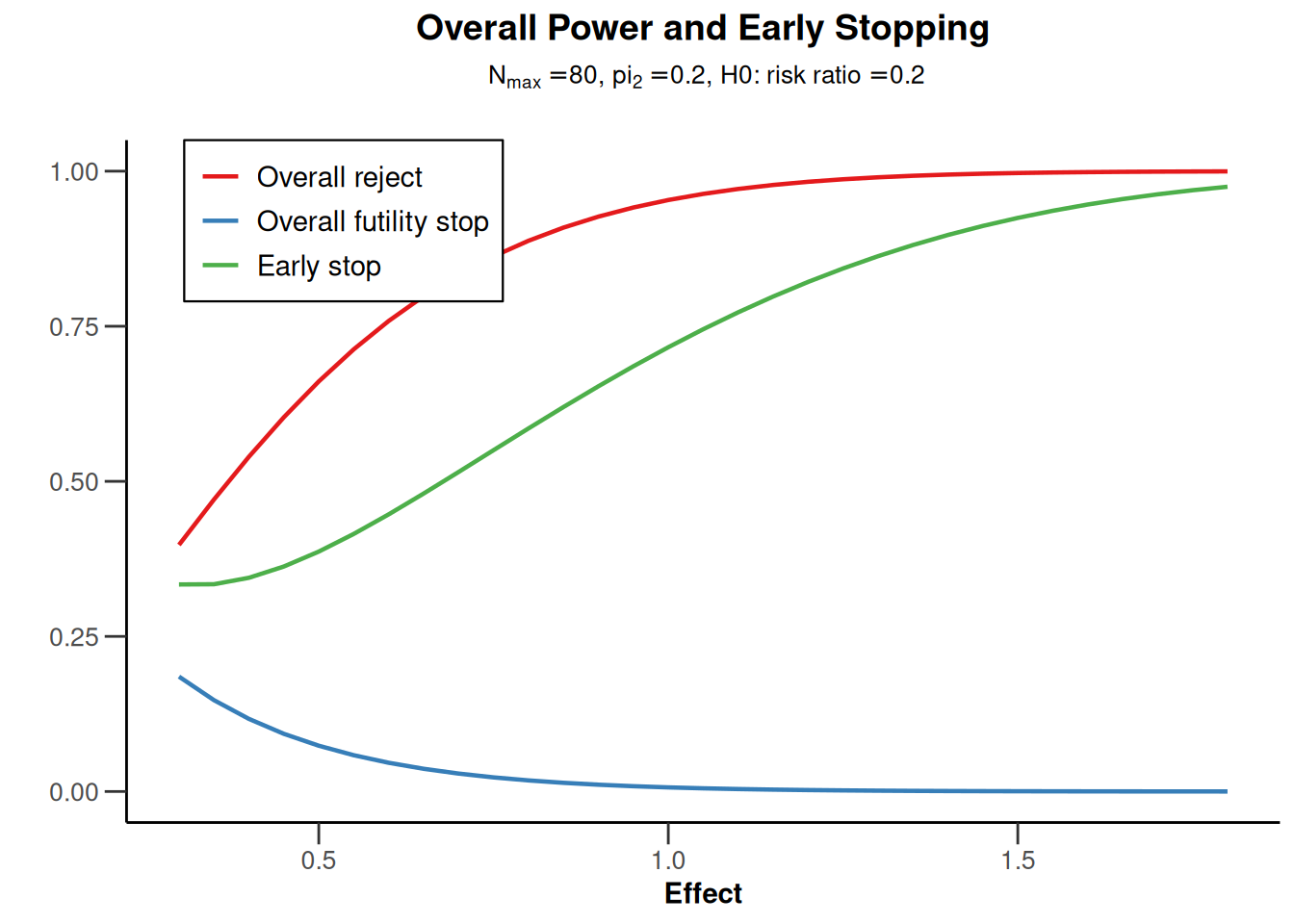

plot(powerRates1, type = 6)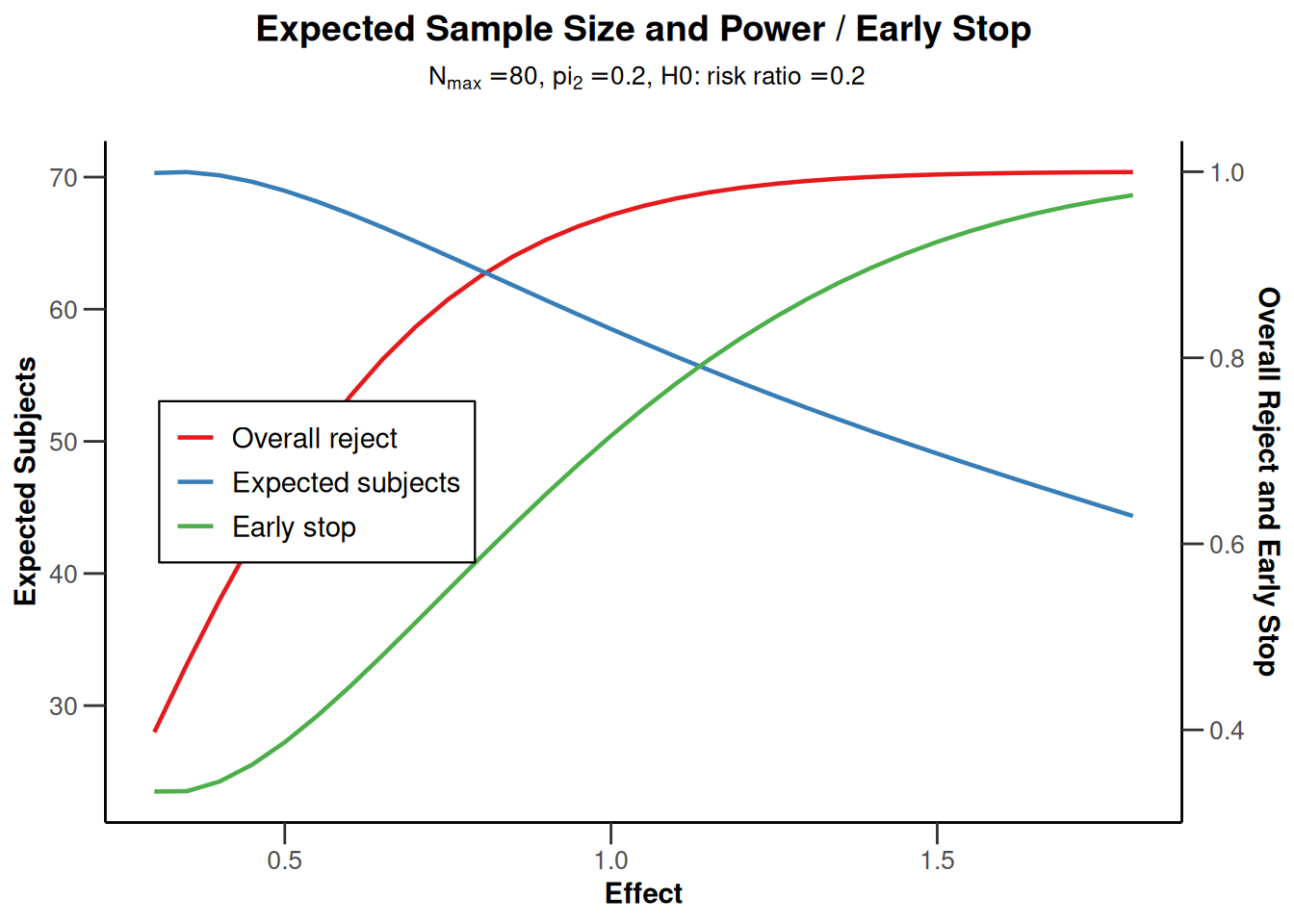

Power rates for a two-sided design

powerRates2 <- getPowerRates(
    getDesignGroupSequential(
        typeOfDesign = "OF", sided = 2, twoSidedPower = TRUE
    ),
    maxNumberOfSubjects = 120
)

plot(powerRates2, type = 1)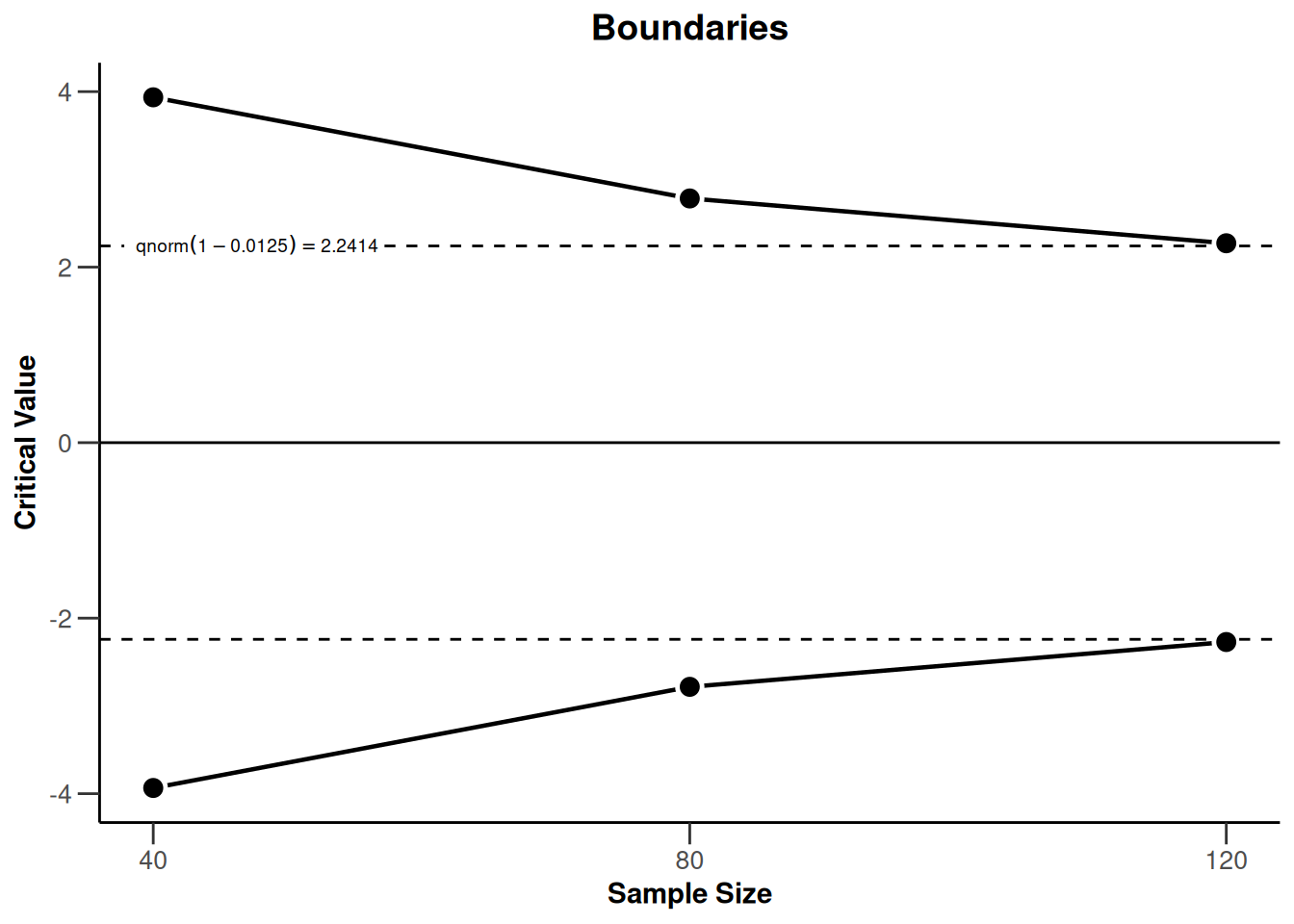

plot(powerRates2, type = 2)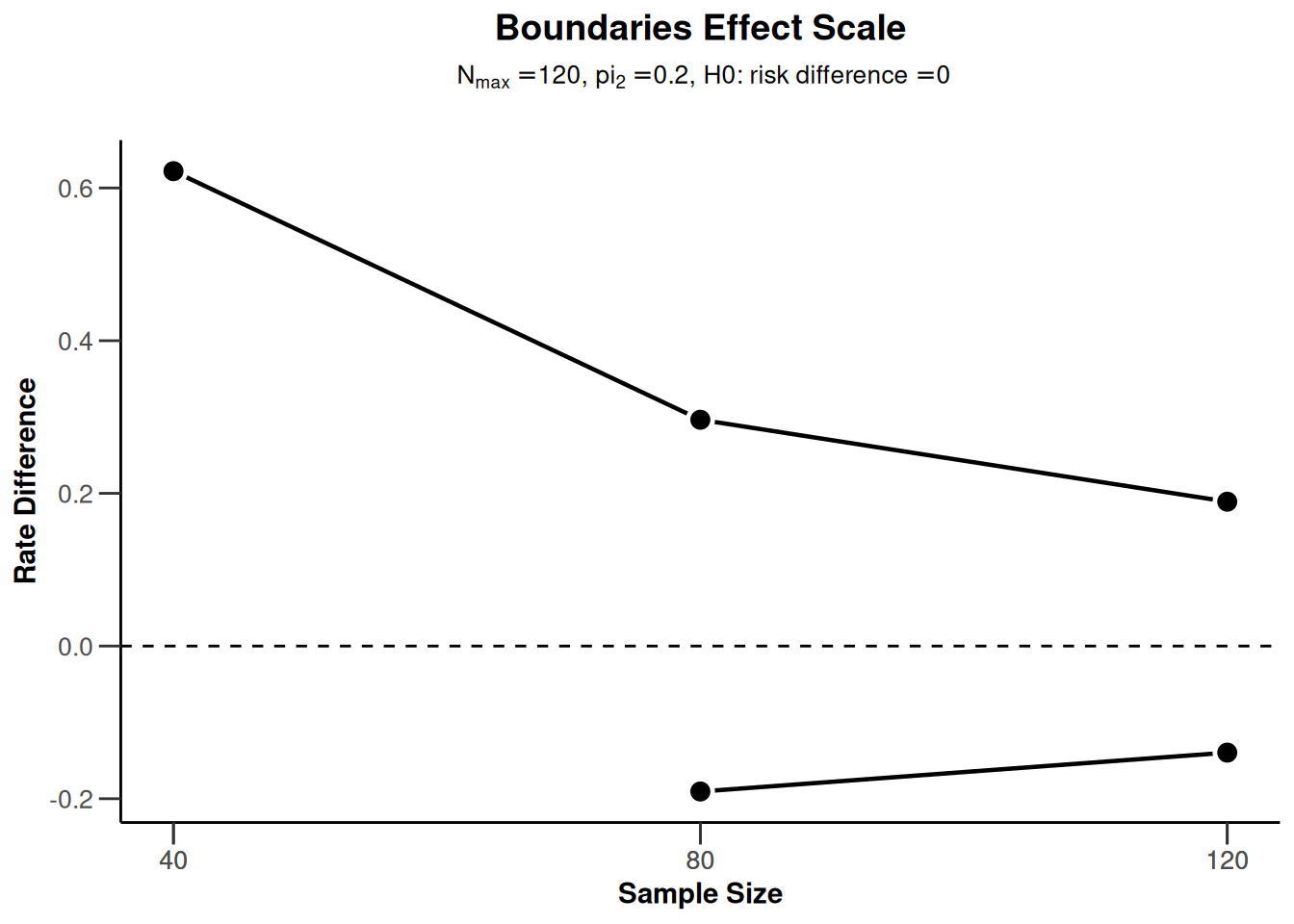

plot(powerRates2, type = 5)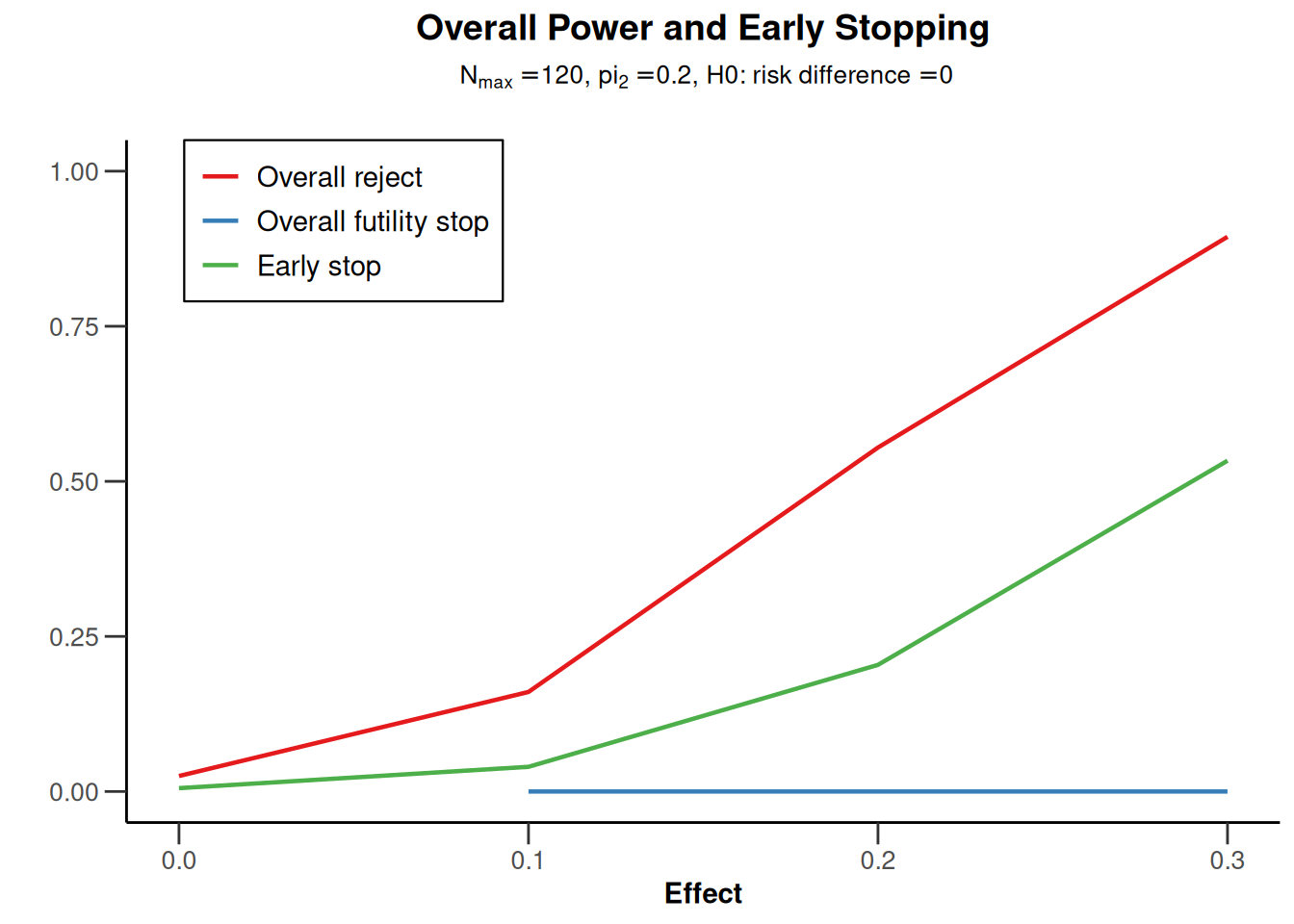

plot(powerRates2, type = 6)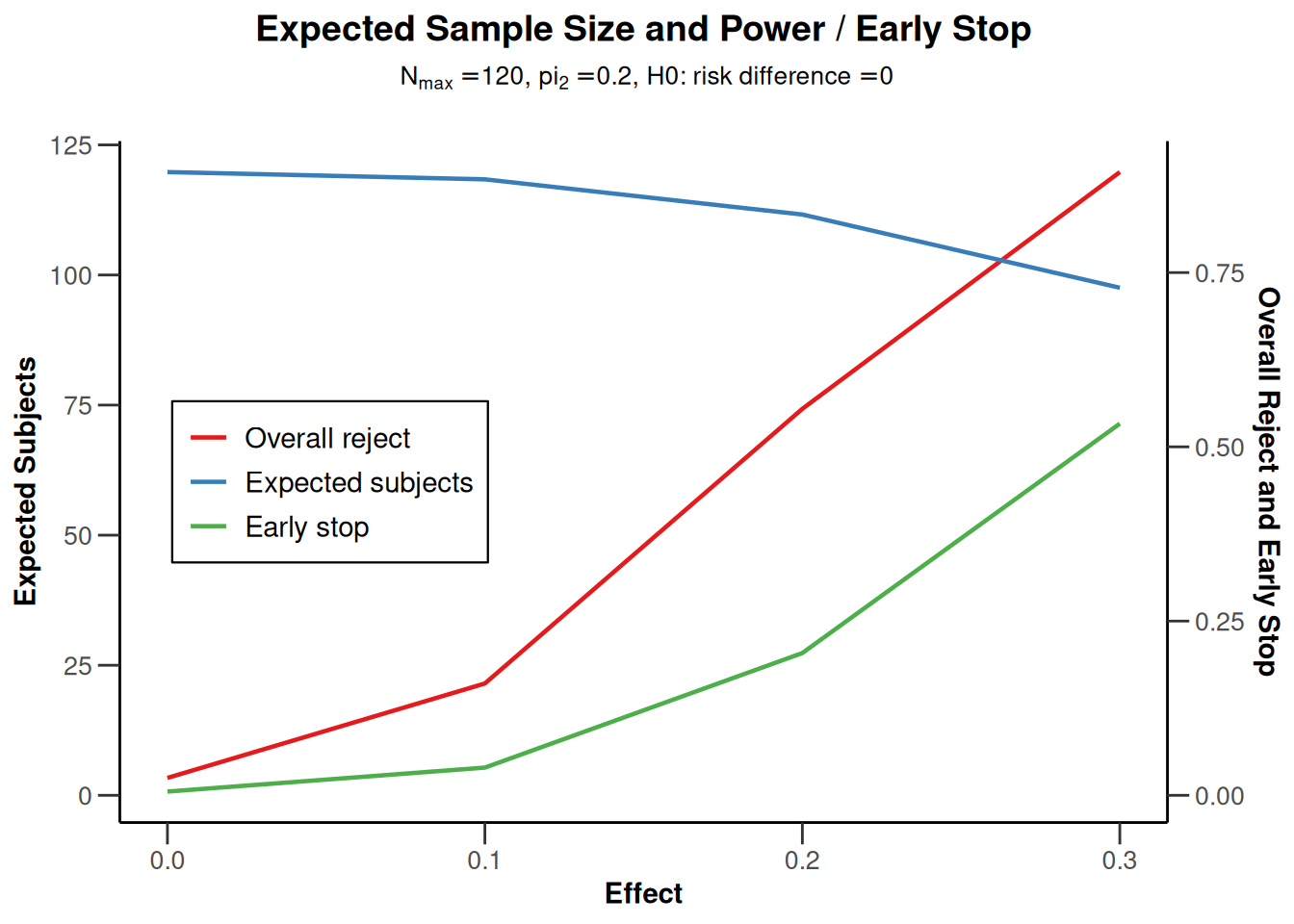

Power survival (survival endpoint)

Power survival for a one-sided design with futility bounds

design <- getDesignGroupSequential(
    kMax = 3,
    typeOfDesign = "OF", sided = 1,
    futilityBounds = c(0, 0)
)

powerSurvival <- getPowerSurvival(
    design = design,
    typeOfComputation = "Schoenfeld", thetaH0 = 1,
    allocationRatioPlanned = 1, kappa = 1,
    maxNumberOfSubjects = 2480,
    maxNumberOfEvents = 70
)

plot(powerSurvival, type = 1)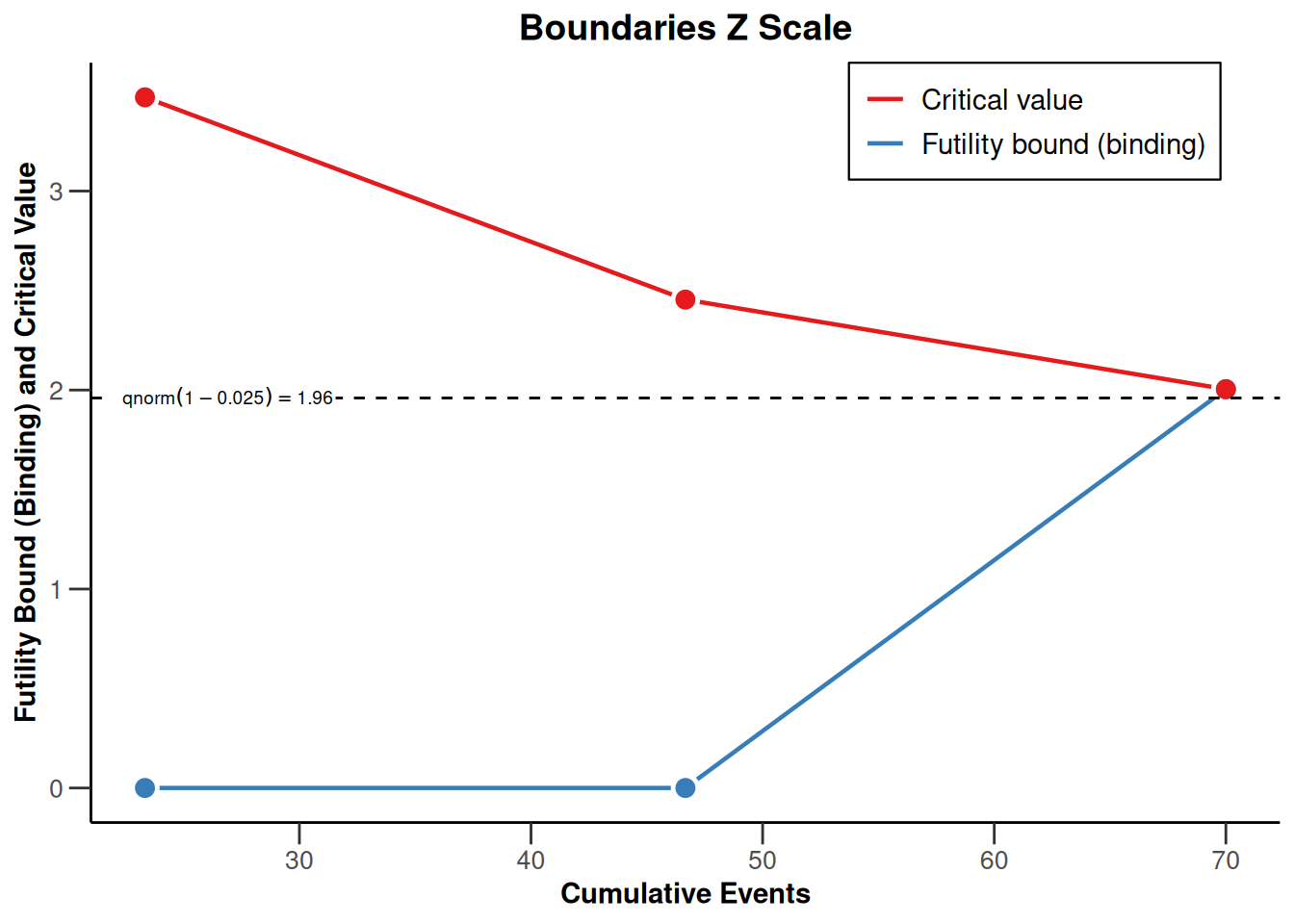

plot(powerSurvival, type = 2)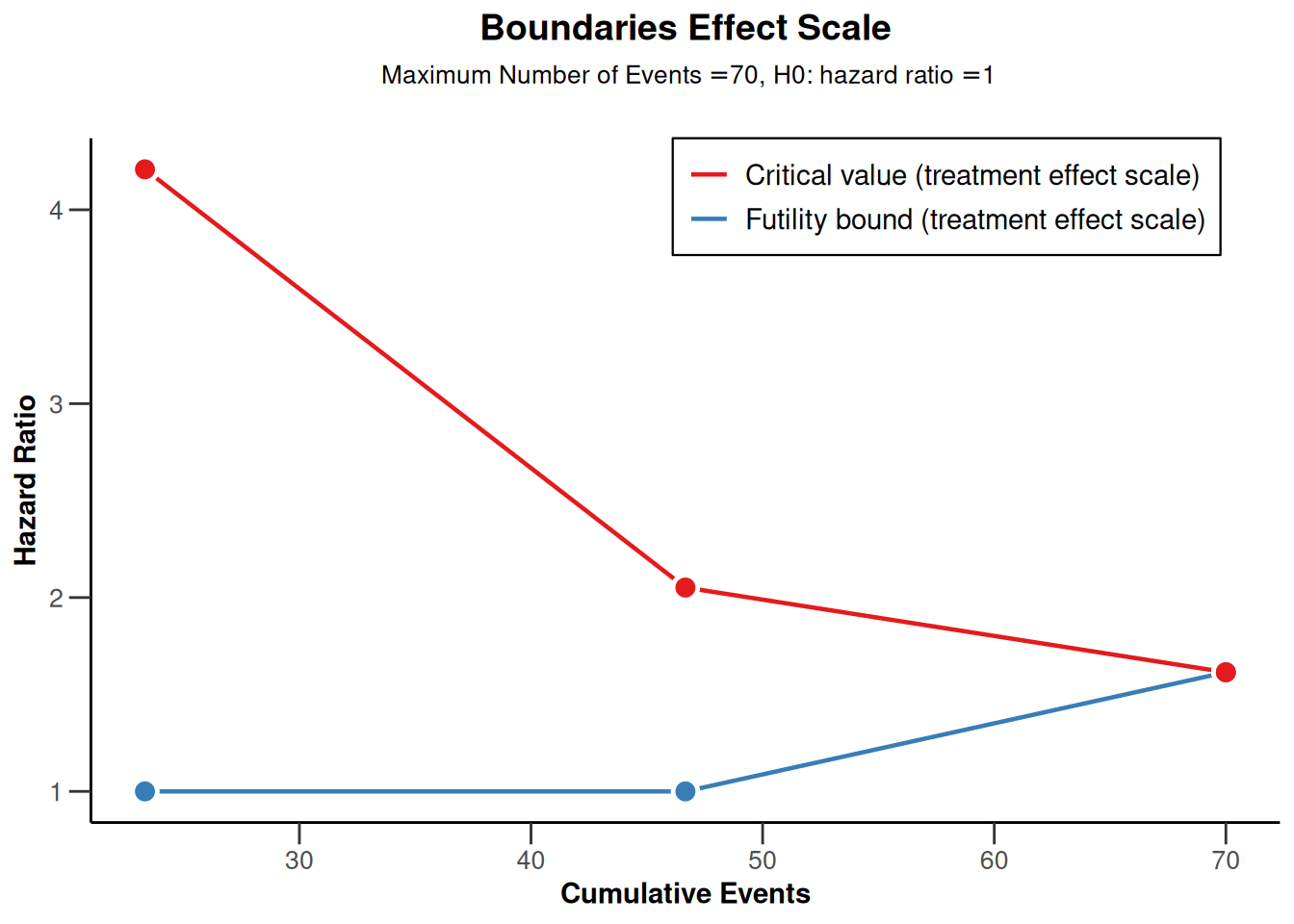

plot(powerSurvival, type = 5)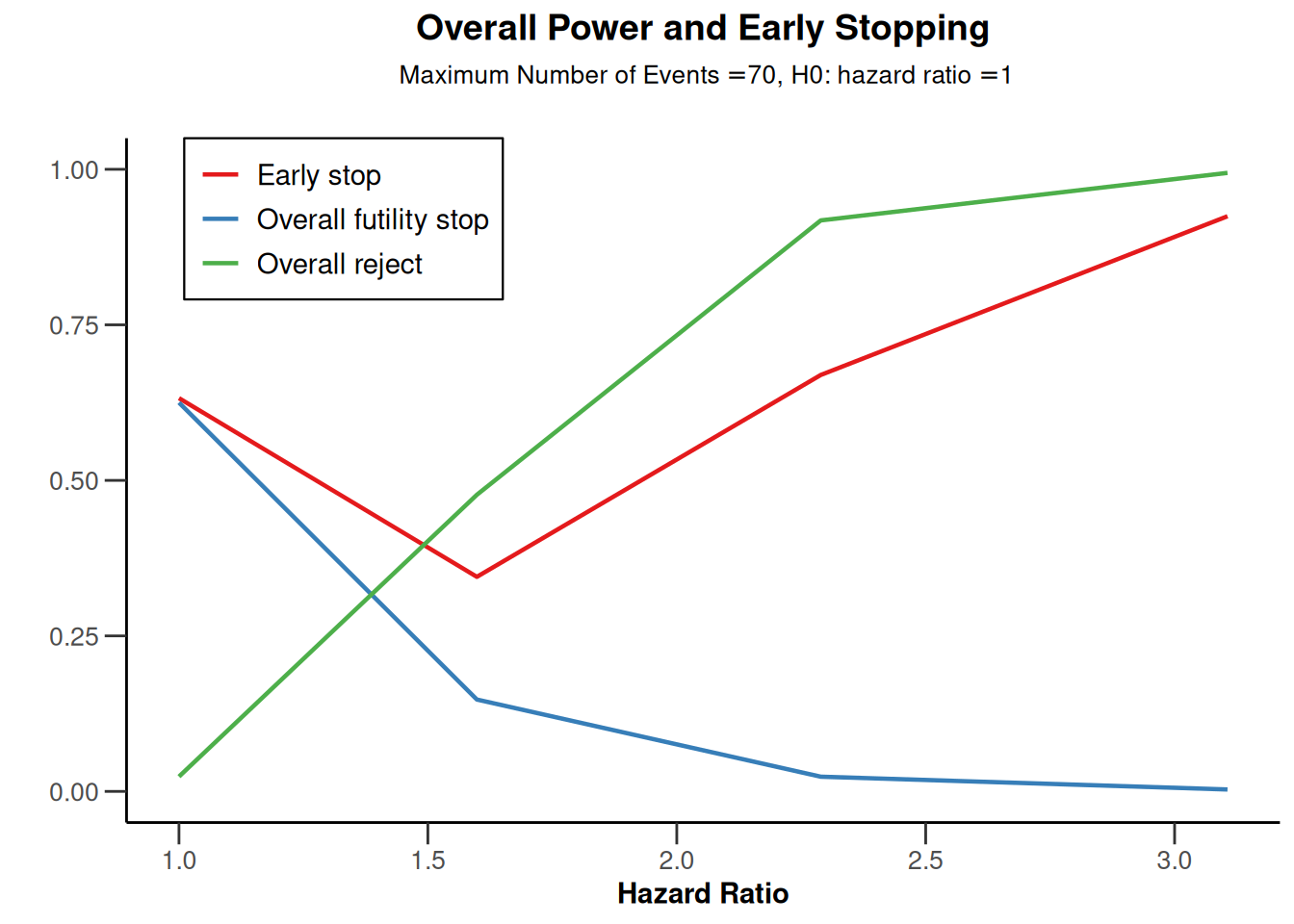

plot(powerSurvival, type = 6)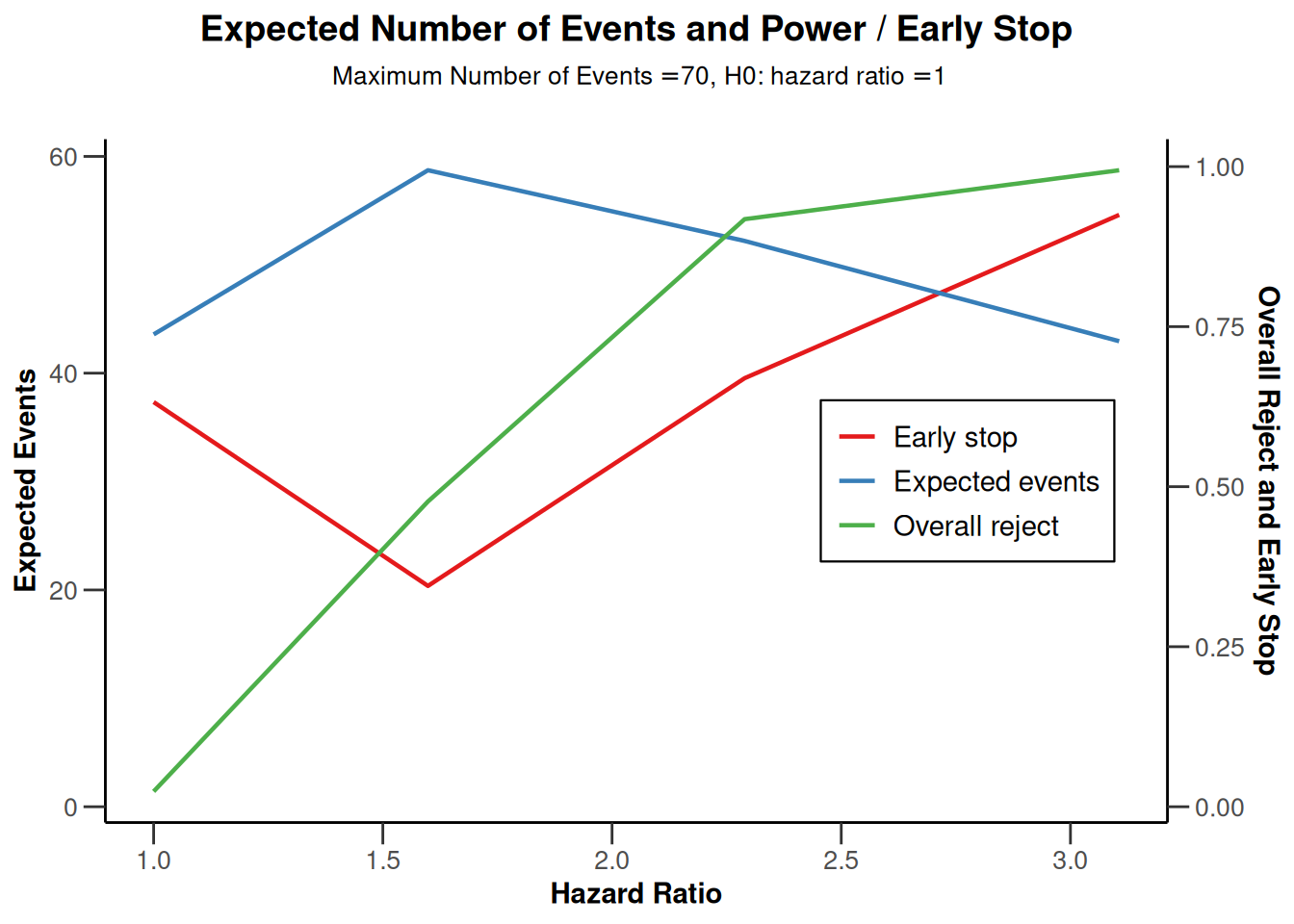

plot(powerSurvival, type = 7)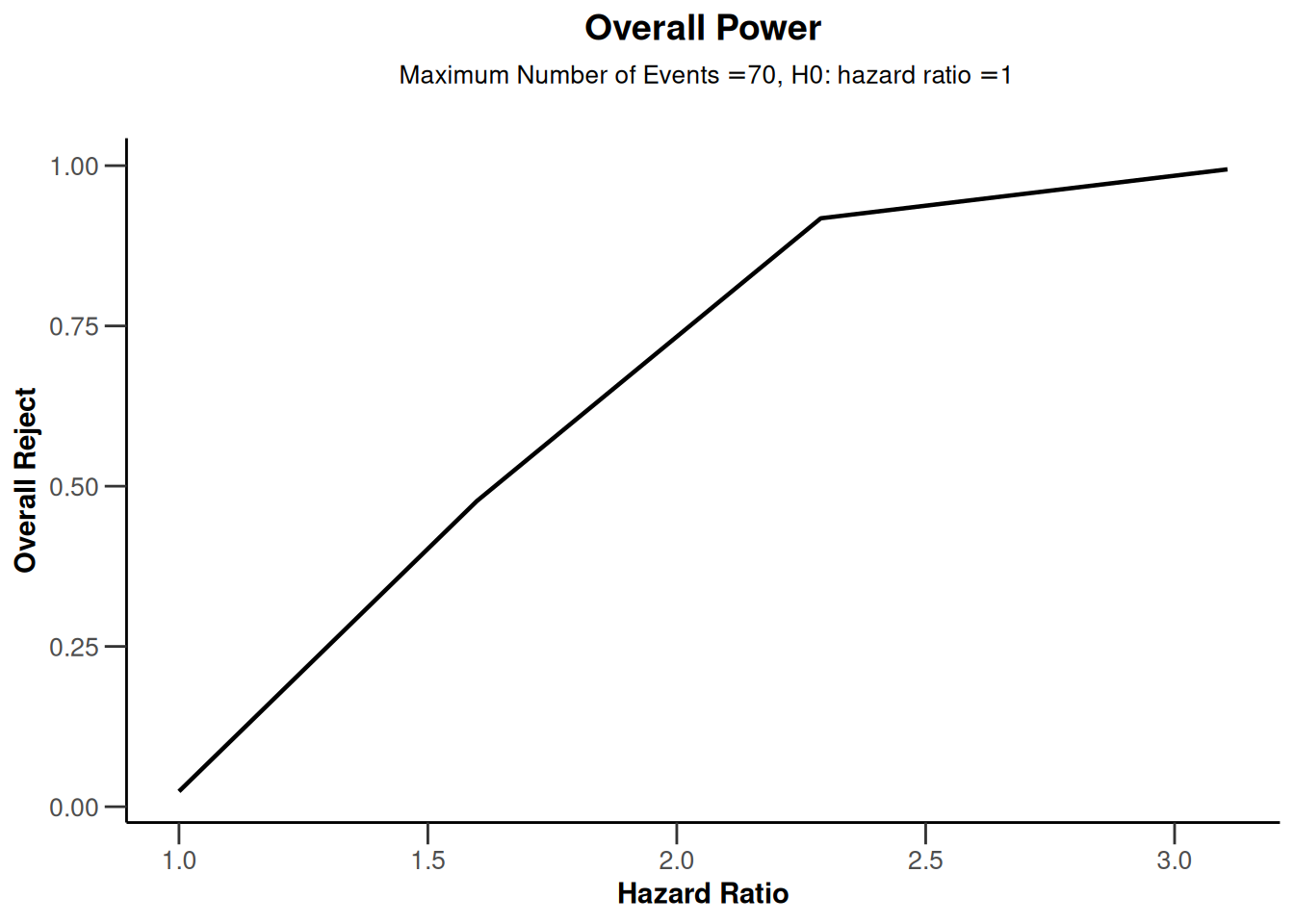

plot(powerSurvival, type = 12)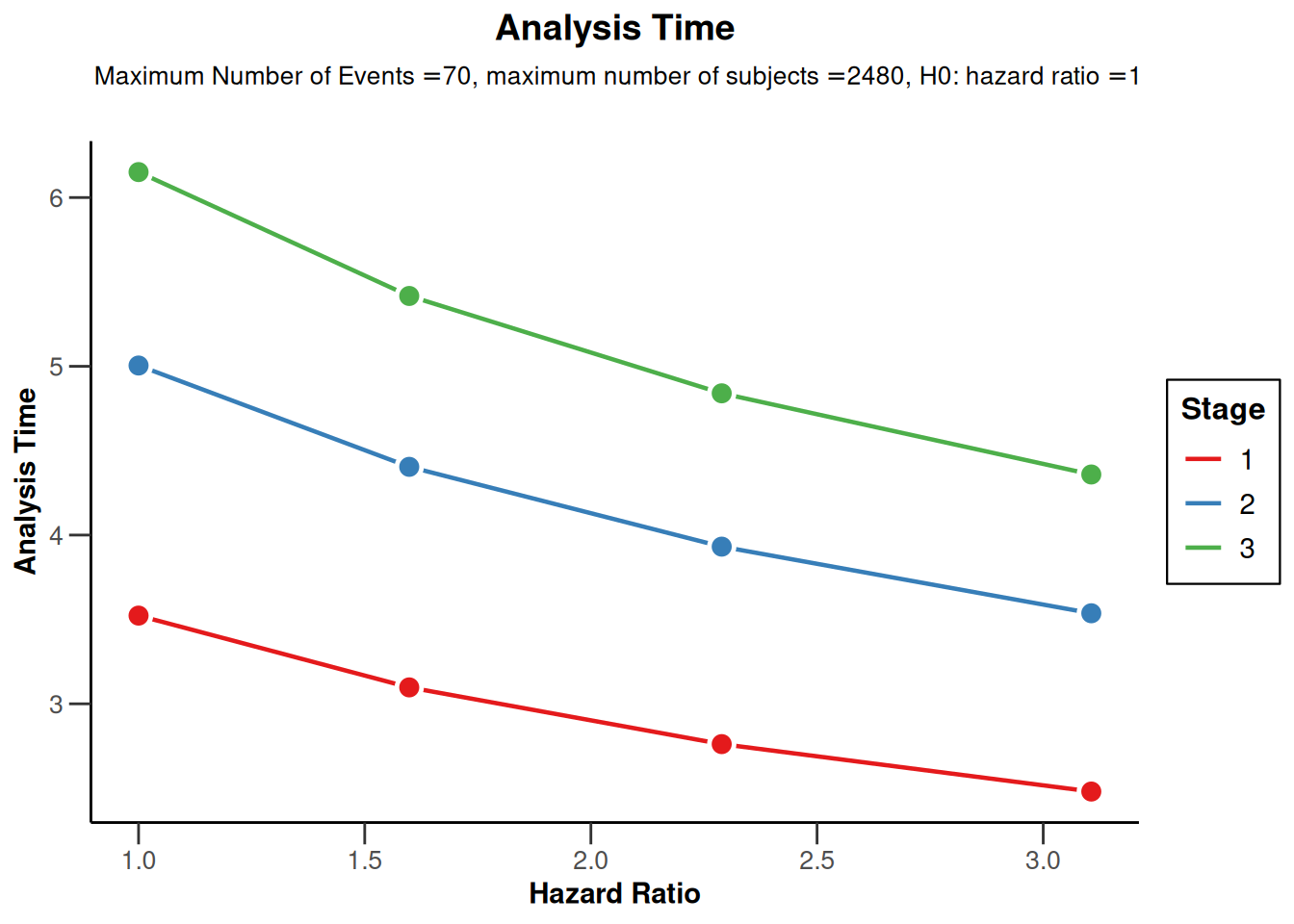

Power for a piecewise exponential survival distribution

design <- getDesignGroupSequential(
    kMax = 3, typeOfDesign = "OF",
    sided = 2, twoSidedPower = TRUE
)
piecewiseSurvivalTime <- list(
    "<5" = 0.04,
    "5 - <10" = 0.02,
    ">= 10" = 0.008
)

powerSurvival1 <- getPowerSurvival(
    design = design,
    typeOfComputation = "Schoenfeld", thetaH0 = 1,
    allocationRatioPlanned = 1, kappa = 1,
    piecewiseSurvivalTime = piecewiseSurvivalTime,
    maxNumberOfSubjects = 2480, maxNumberOfEvents = 70,
    hazardRatio = c(0.5, 2)
)

plot(powerSurvival1, type = 1)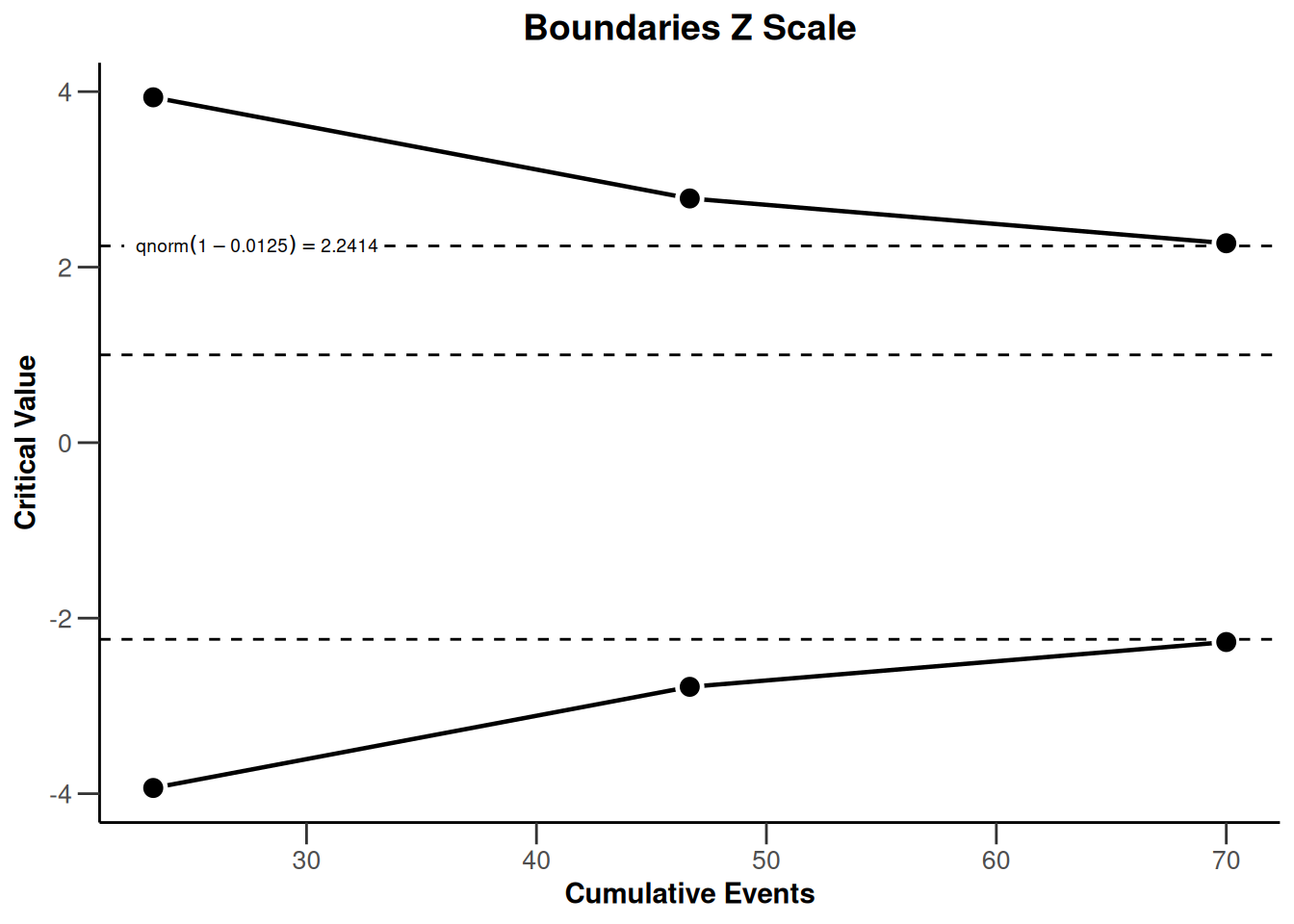

plot(powerSurvival1, type = 2)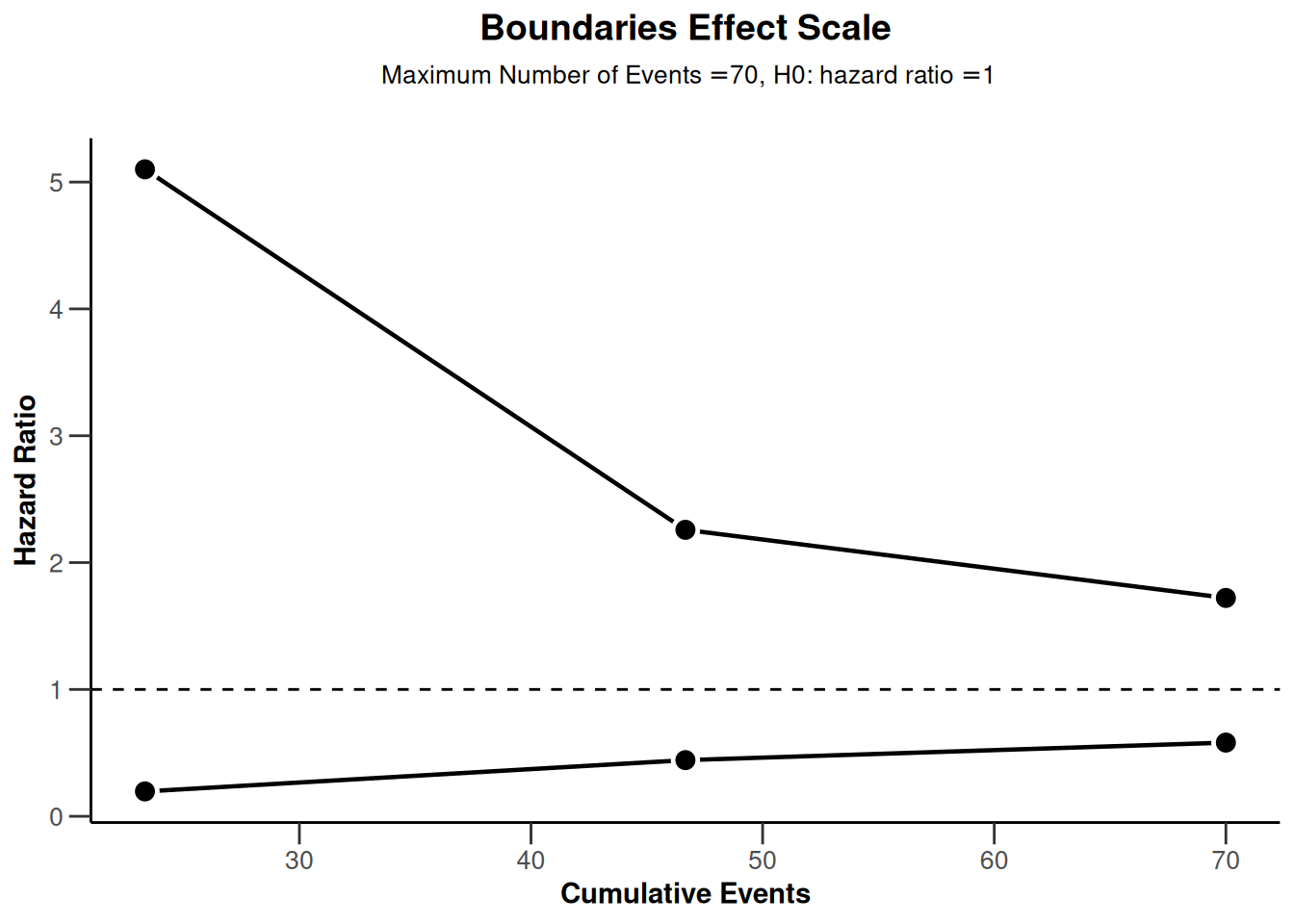

plot(powerSurvival1, type = 12)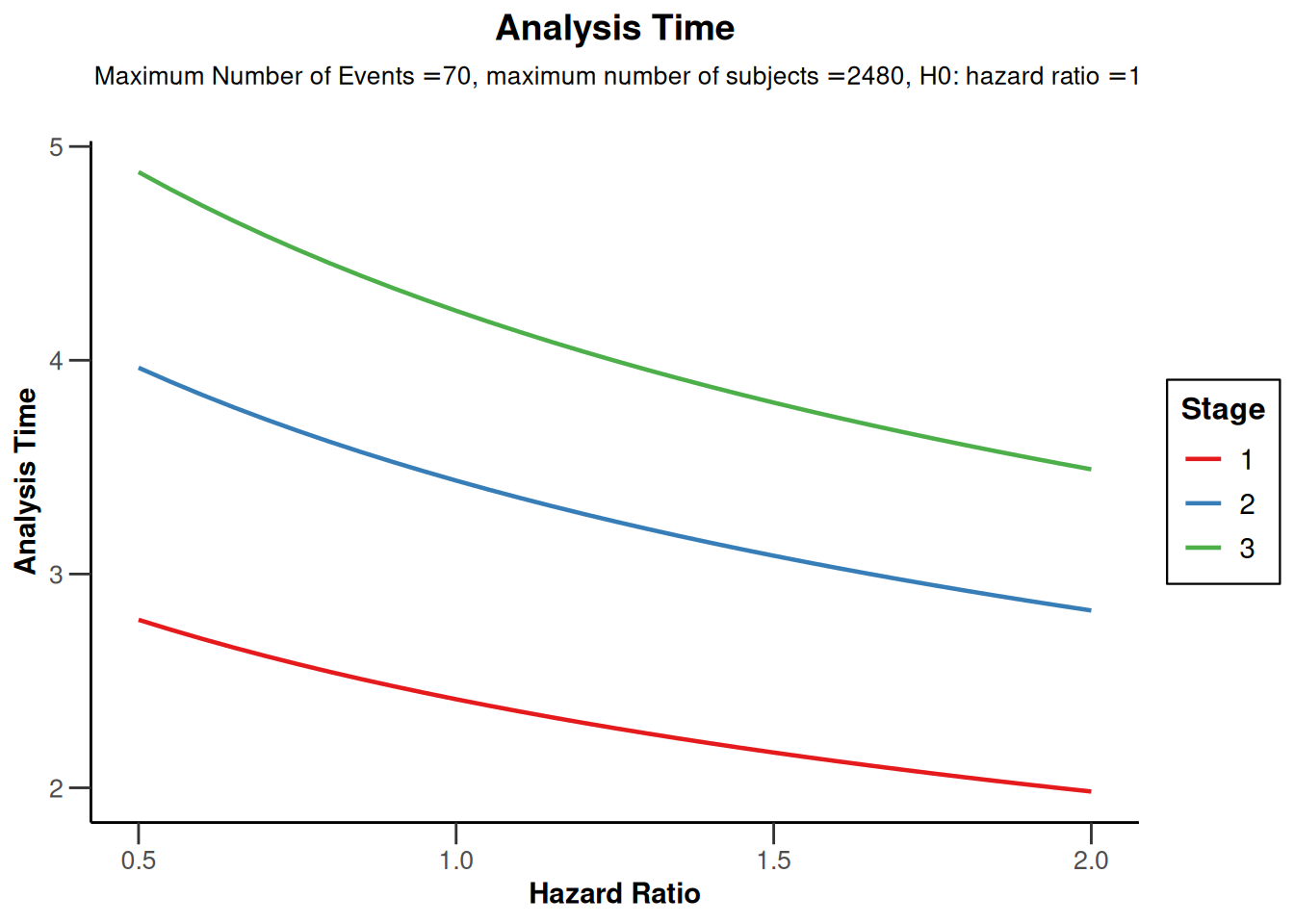

plot(powerSurvival1, type = 13, legendPosition = 1)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting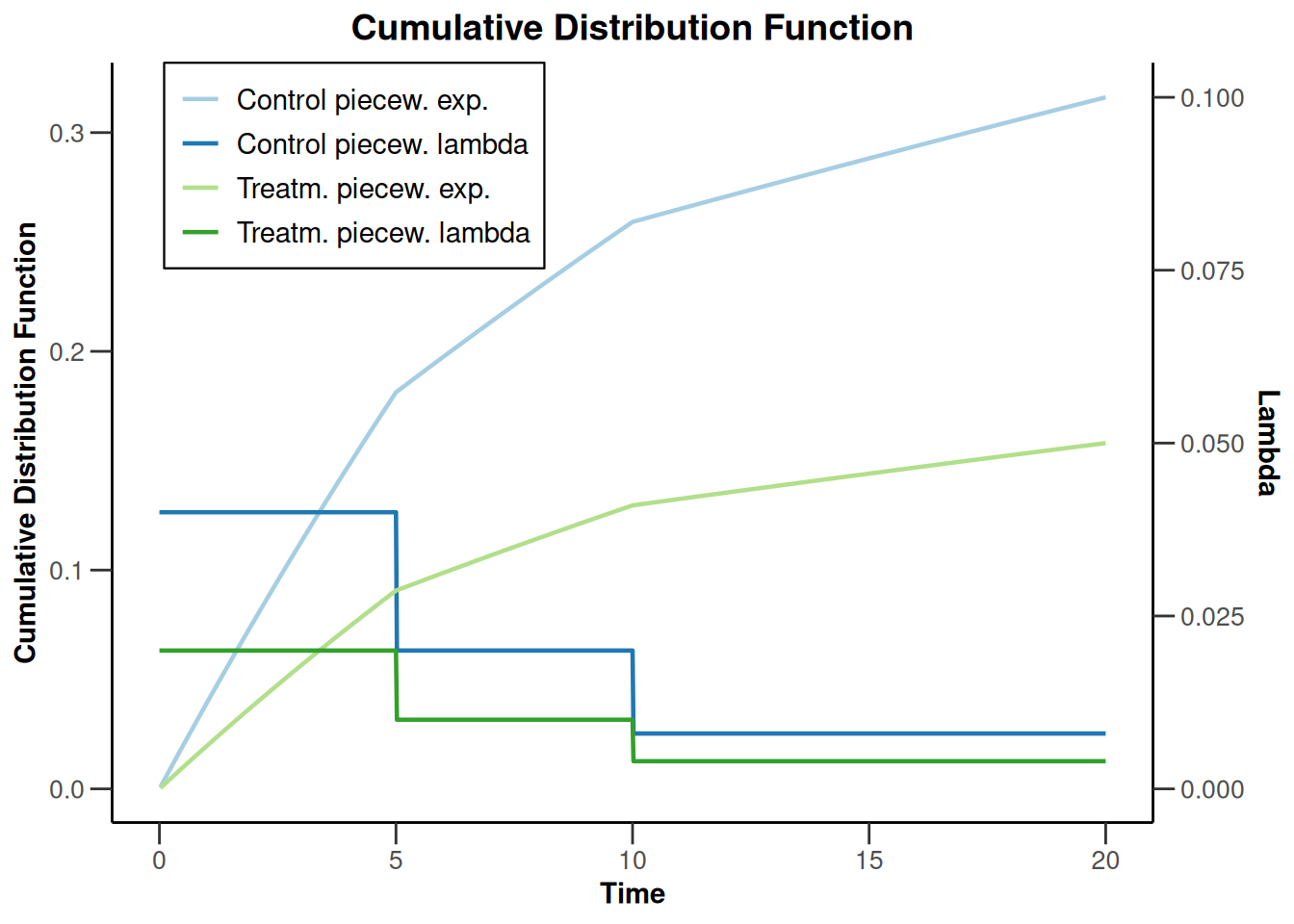

plot(powerSurvival1, type = 14, legendPosition = 5)

Warning: Only the first 'hazardRatio' (0.5) was used for plotting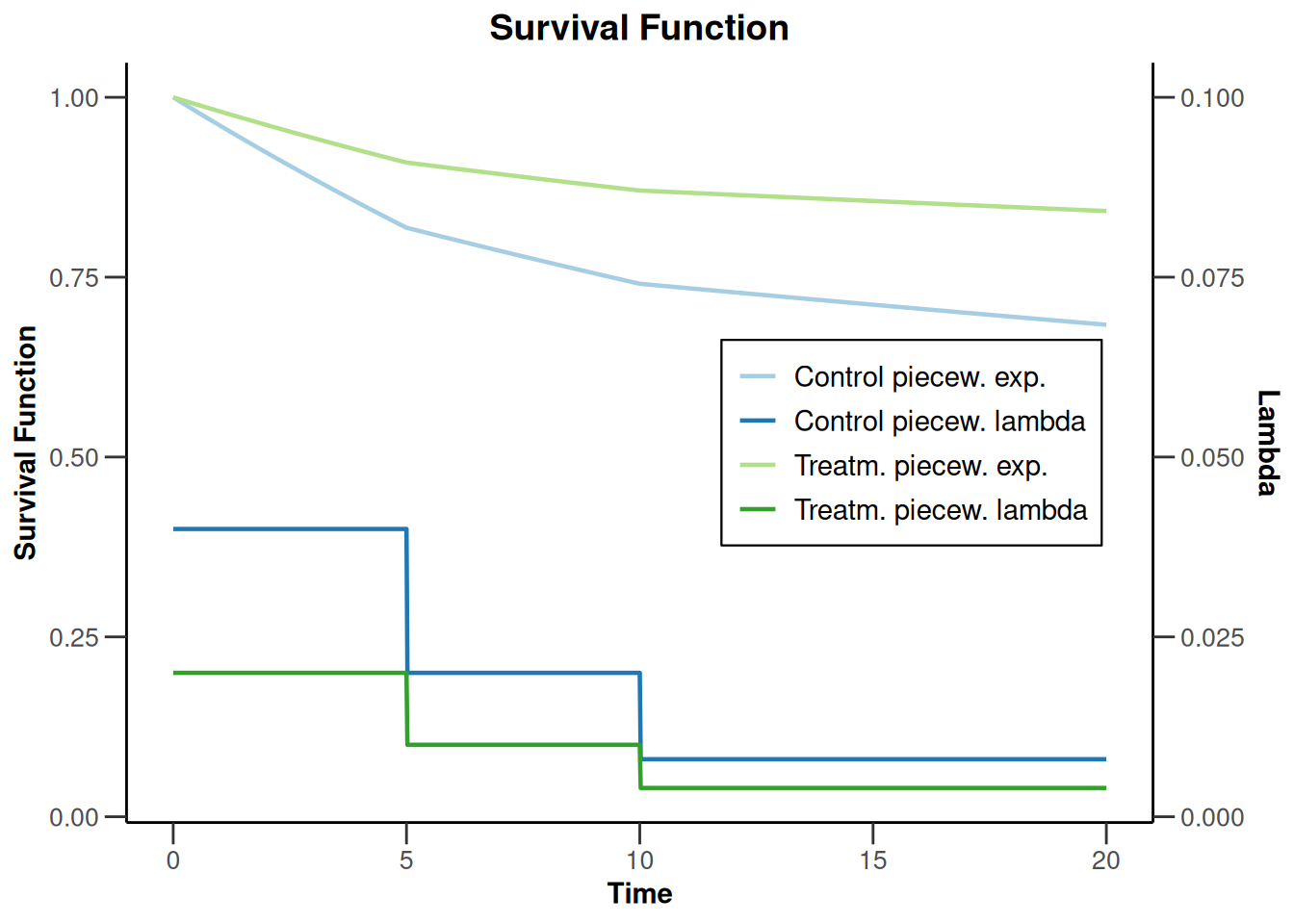

Power for a piecewise exponential survival distribution and a design with futility bounds

design <- getDesignGroupSequential(
    typeOfDesign = "OF", sided = 1,
    futilityBounds = c(0, 0.1)
)

piecewiseSurvivalTime <- list(
    "0 - <6" = 0.025,
    "6 - <9" = 0.04,
    "9 - <15" = 0.015,
    "15 - <21" = 0.01,
    ">= 21" = 0.007
)

powerSurvival2 <- getPowerSurvival(
    design = design,
    typeOfComputation = "Schoenfeld", thetaH0 = 1,
    allocationRatioPlanned = 1, kappa = 1,
    piecewiseSurvivalTime = piecewiseSurvivalTime,
    maxNumberOfSubjects = 2480, maxNumberOfEvents = 70,
    hazardRatio = 0.8
)
plot(powerSurvival2, type = 1)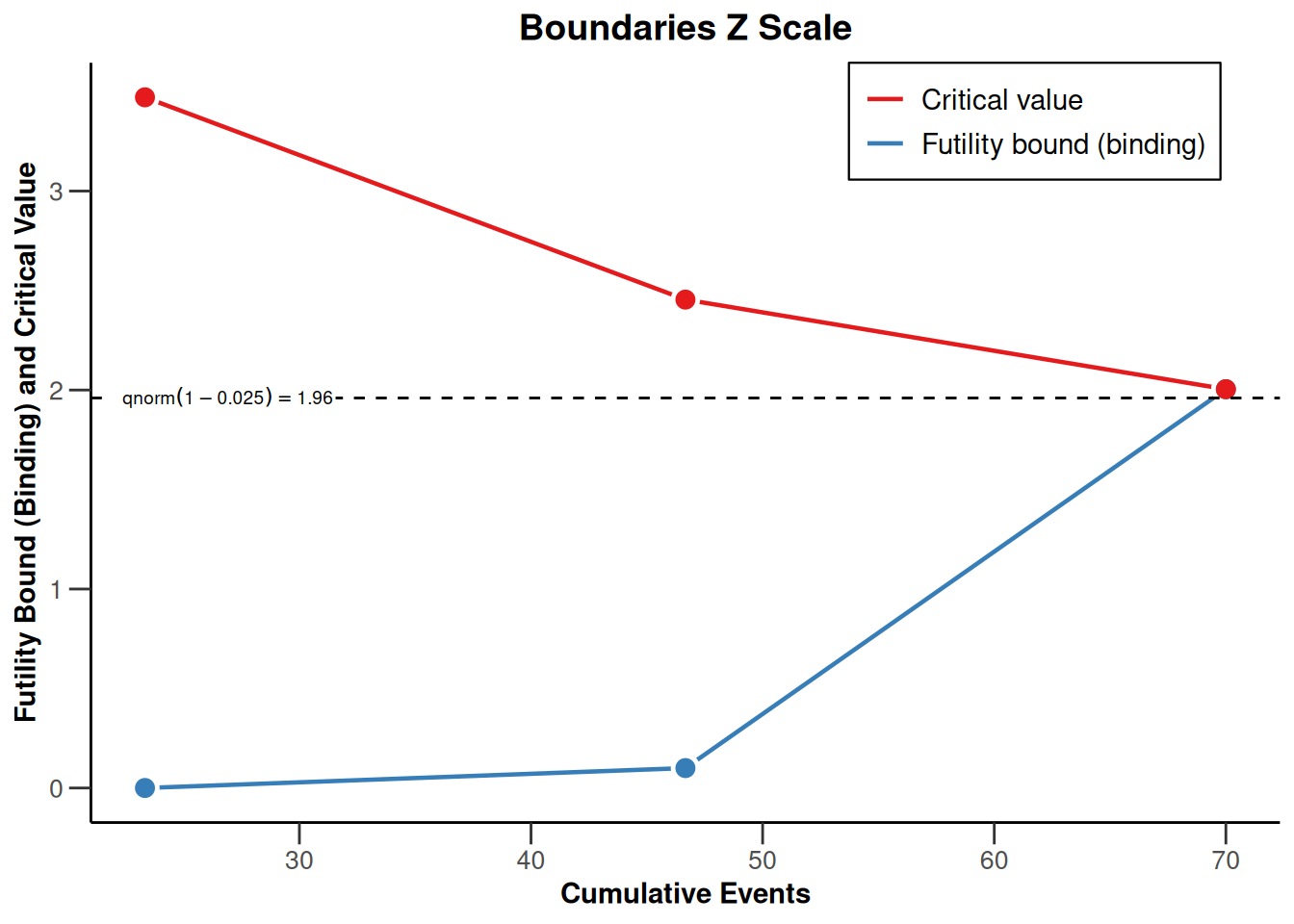

plot(powerSurvival2, type = 2)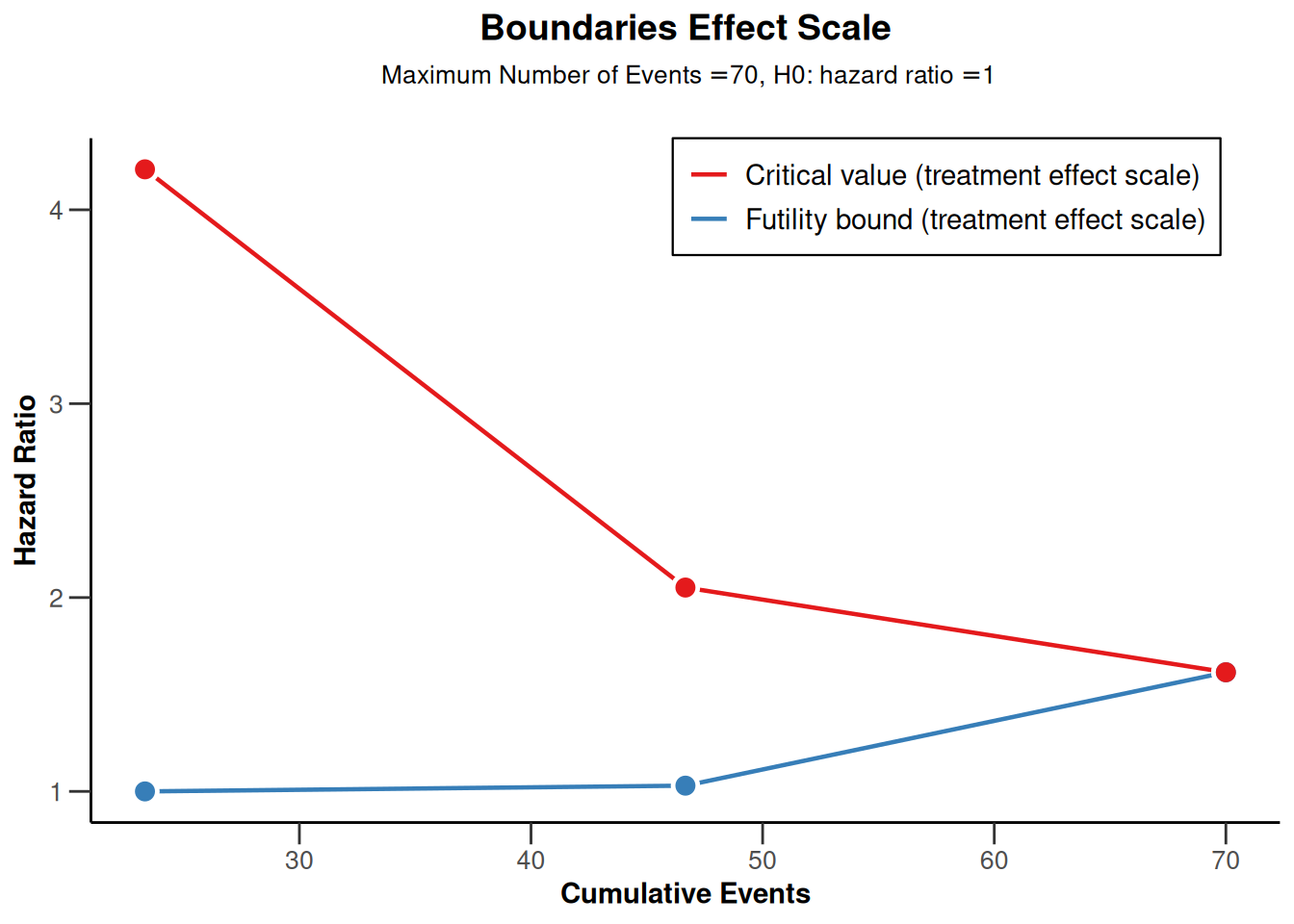

plot(powerSurvival2, type = 13, legendPosition = 1)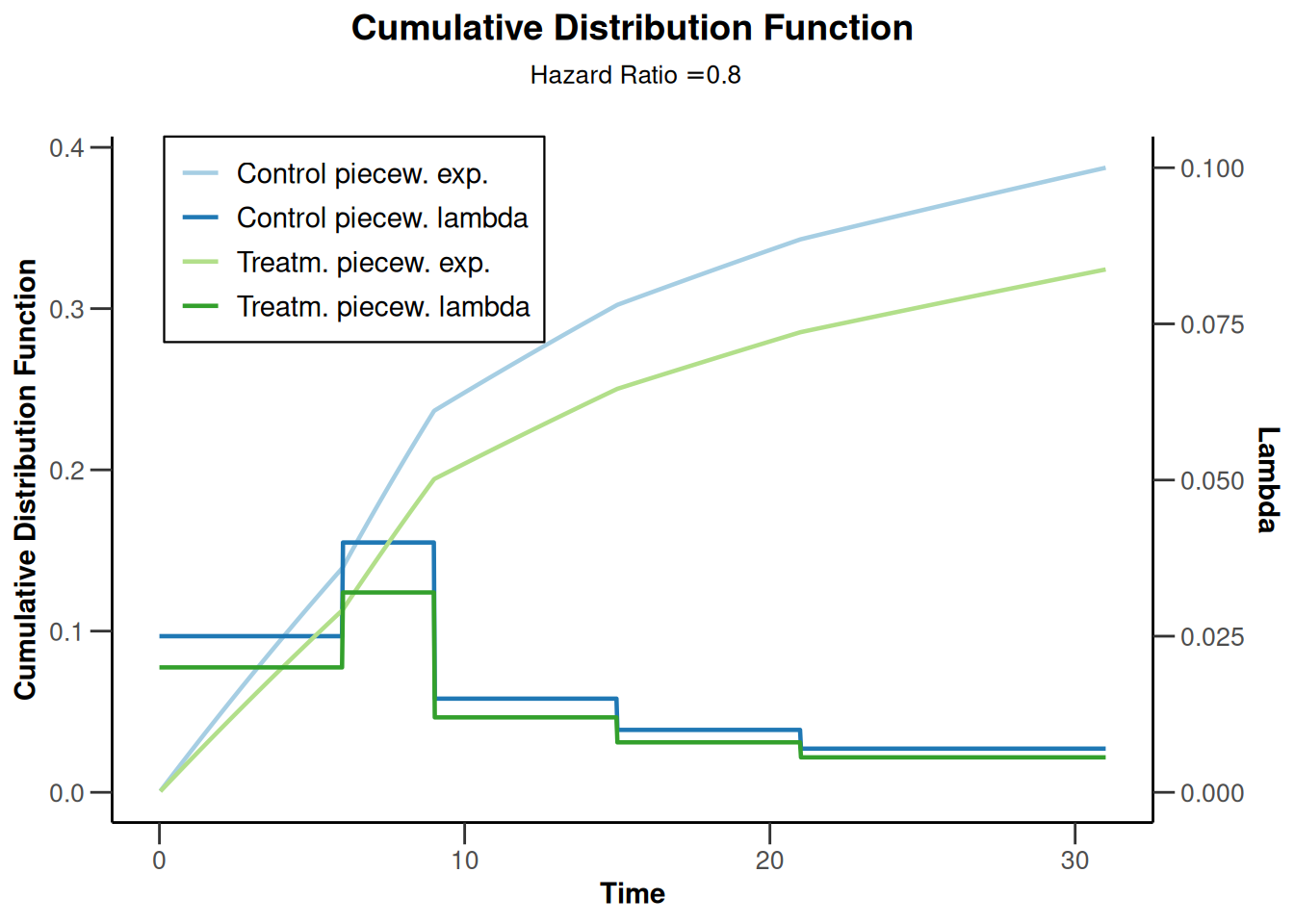

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

plot(powerSurvival2, type = 14)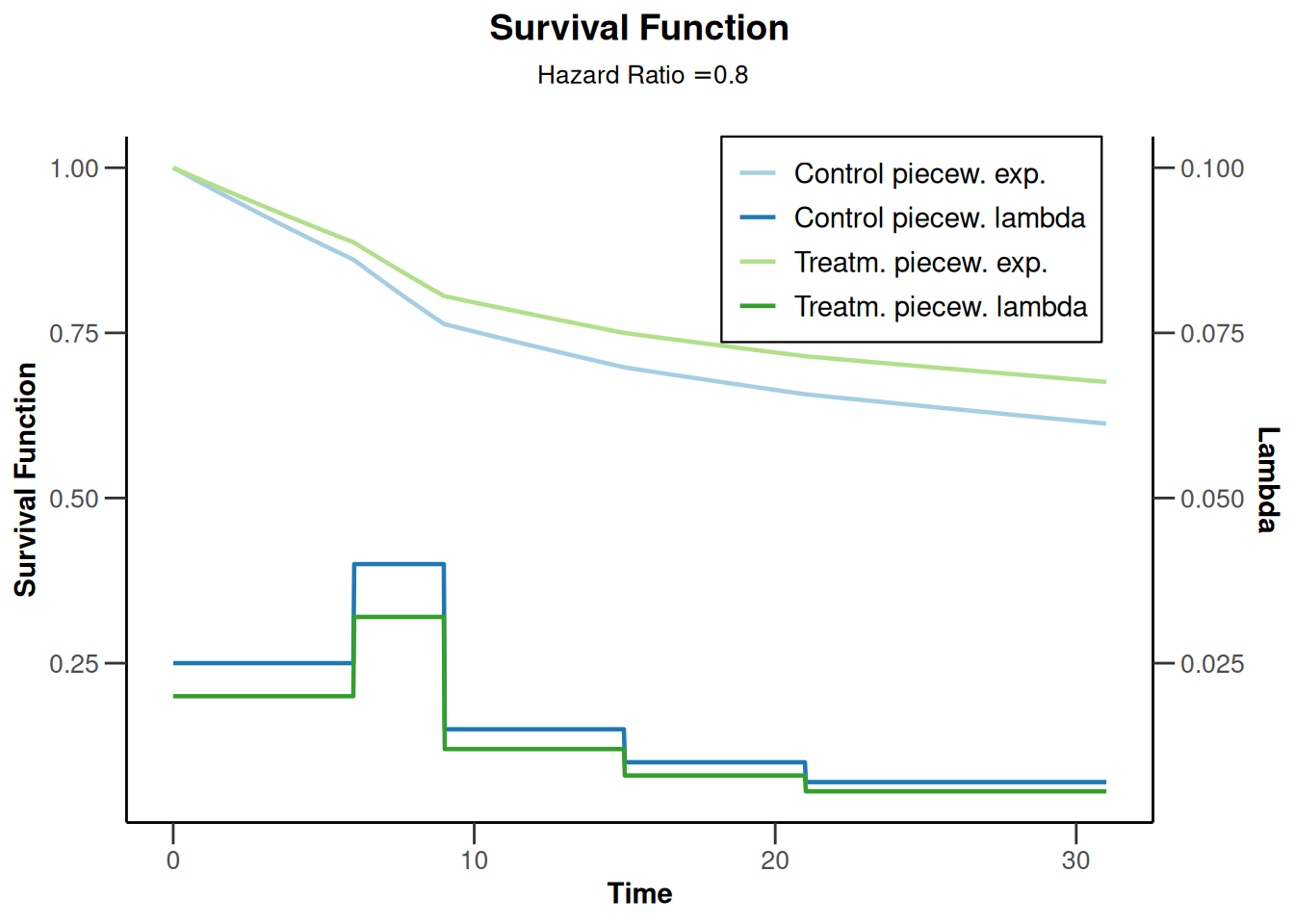

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

design <- getDesignGroupSequential(
    typeOfDesign = "OF", sided = 1,
    futilityBounds = c(0, 0.1)
)

powerSurvival3 <- getPowerSurvival(
    design = design,
    typeOfComputation = "Schoenfeld", thetaH0 = 1,
    allocationRatioPlanned = 1, kappa = 1,
    piecewiseSurvivalTime = c(0, 5, 10),
    lambda2 = c(0.025, 0.04, 0.015),
    lambda1 = c(0.02, 0.032, 0.012),
    maxNumberOfSubjects = 2480, maxNumberOfEvents = 70
)

plot(powerSurvival3, type = 1)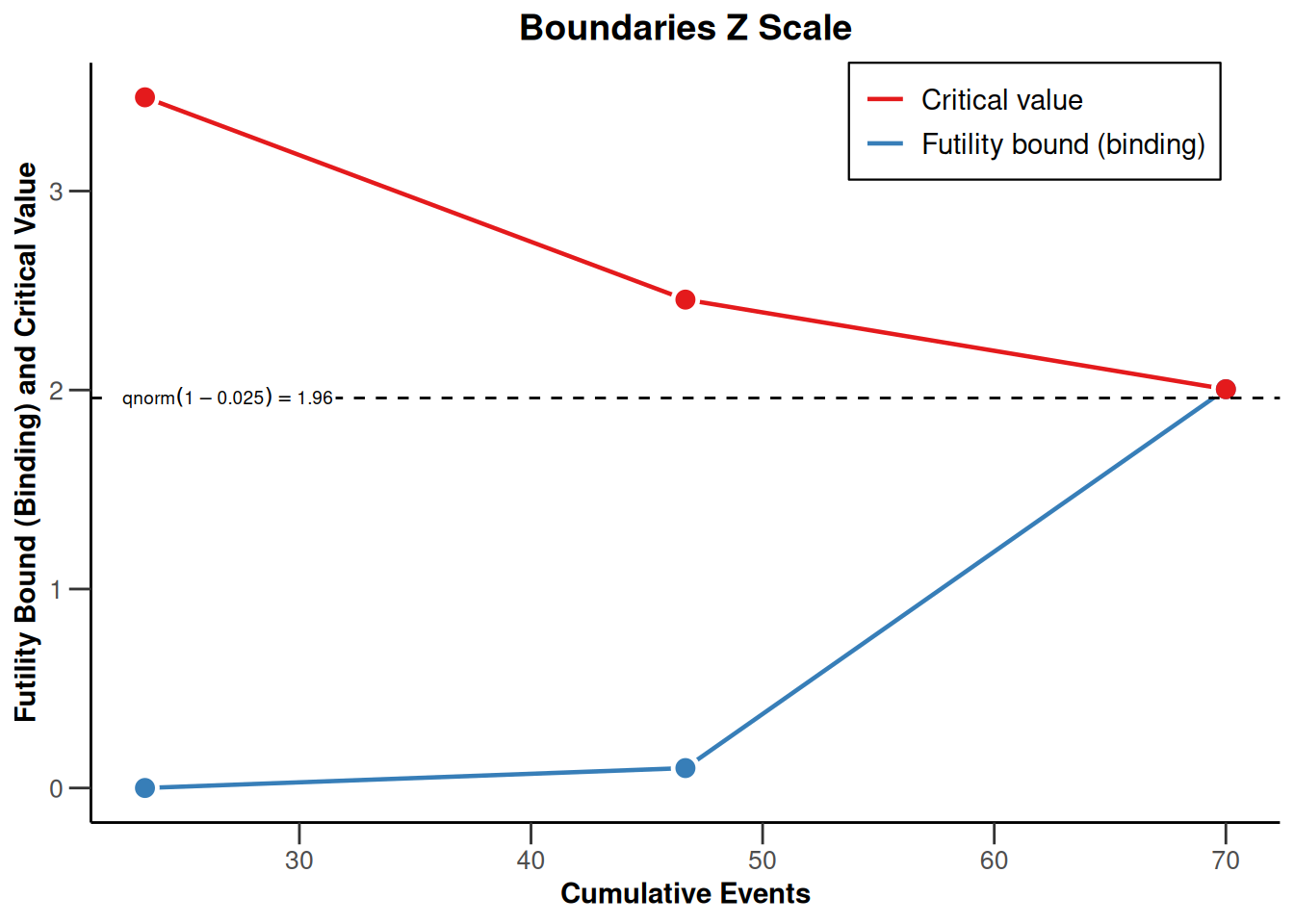

plot(powerSurvival3, type = 2)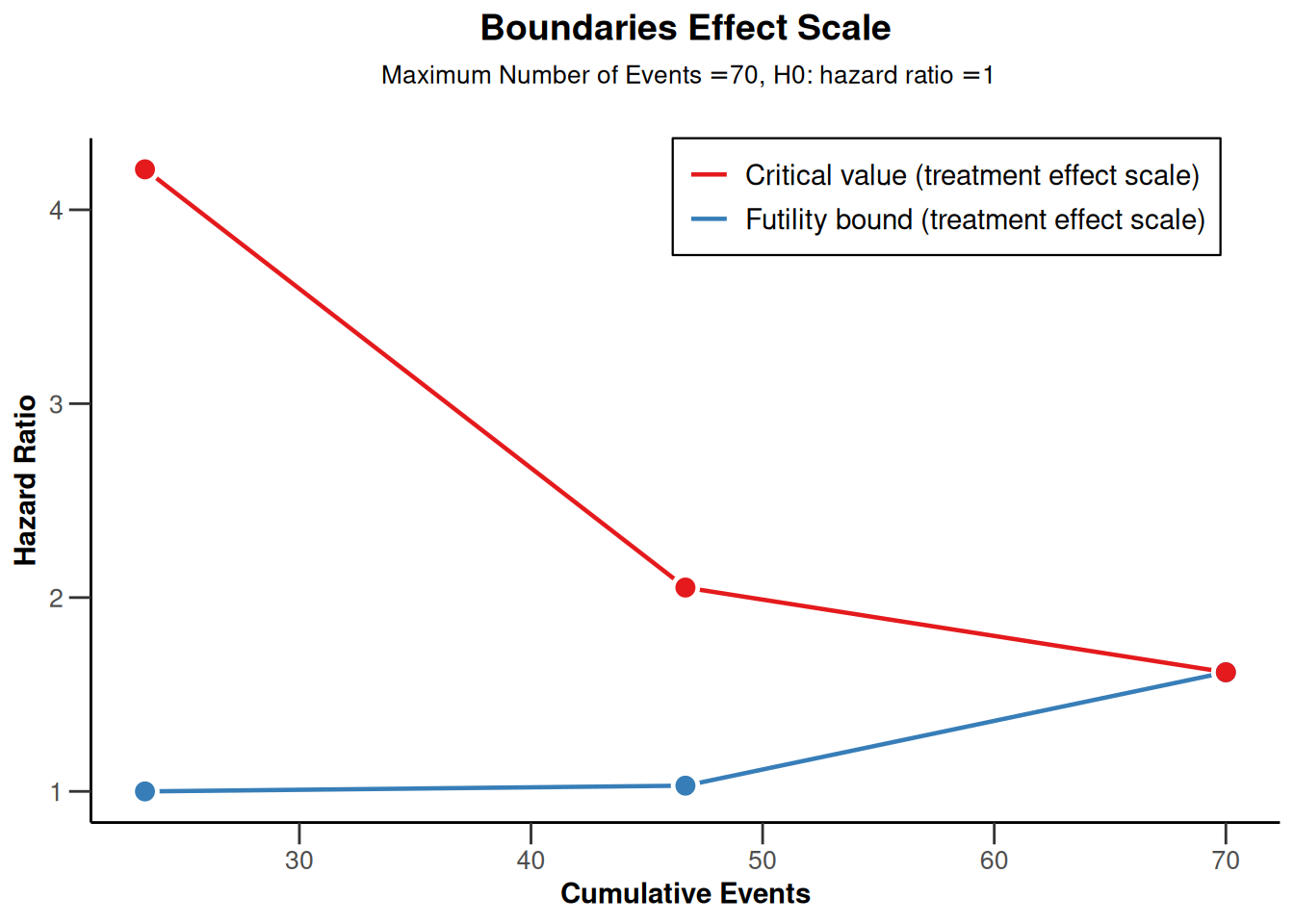

plot(powerSurvival3, type = 13, legendPosition = 1)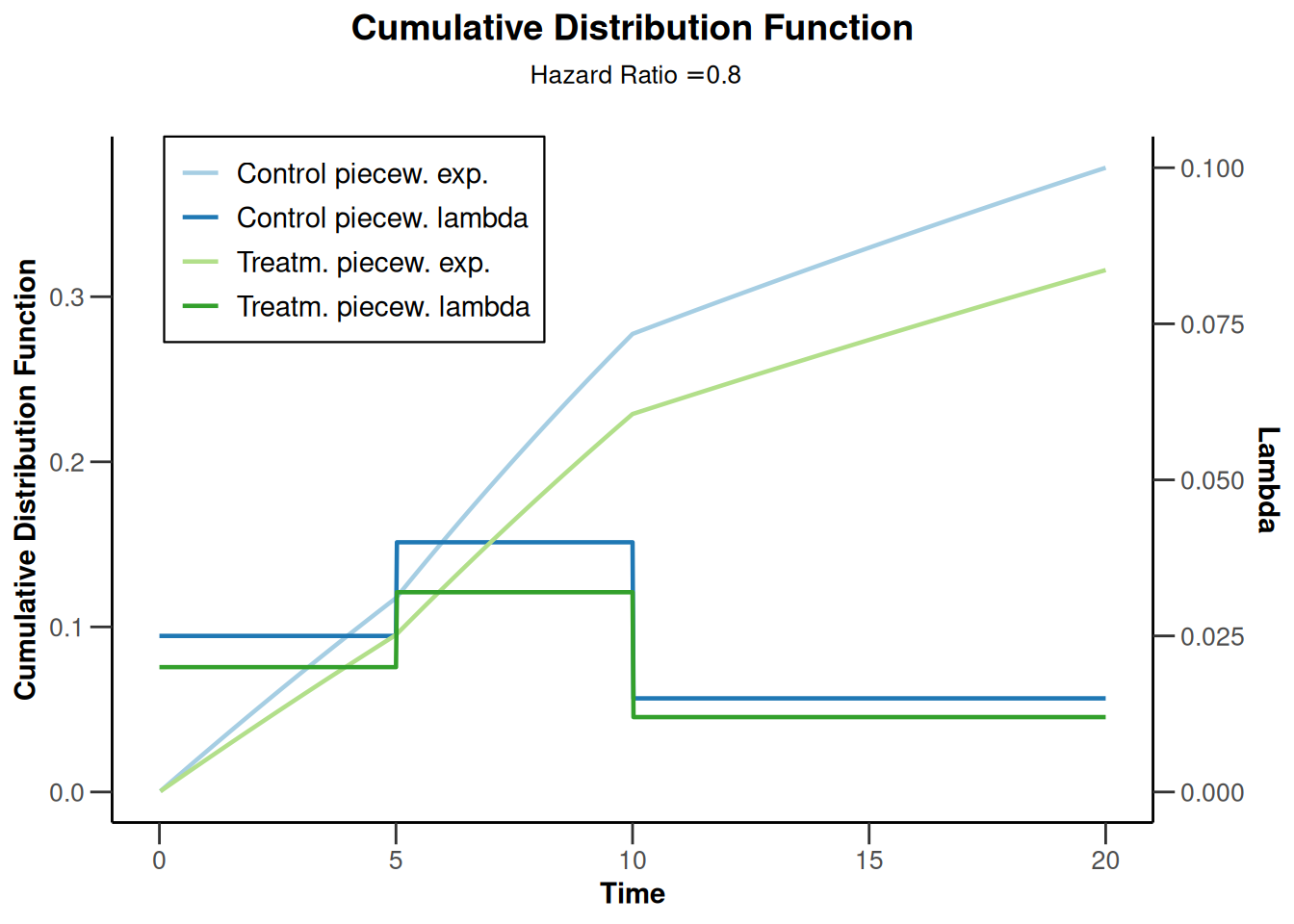

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 3 > 1' in
coercion to 'logical(1)'

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 3 > 1' in
coercion to 'logical(1)'

plot(powerSurvival2, type = 14)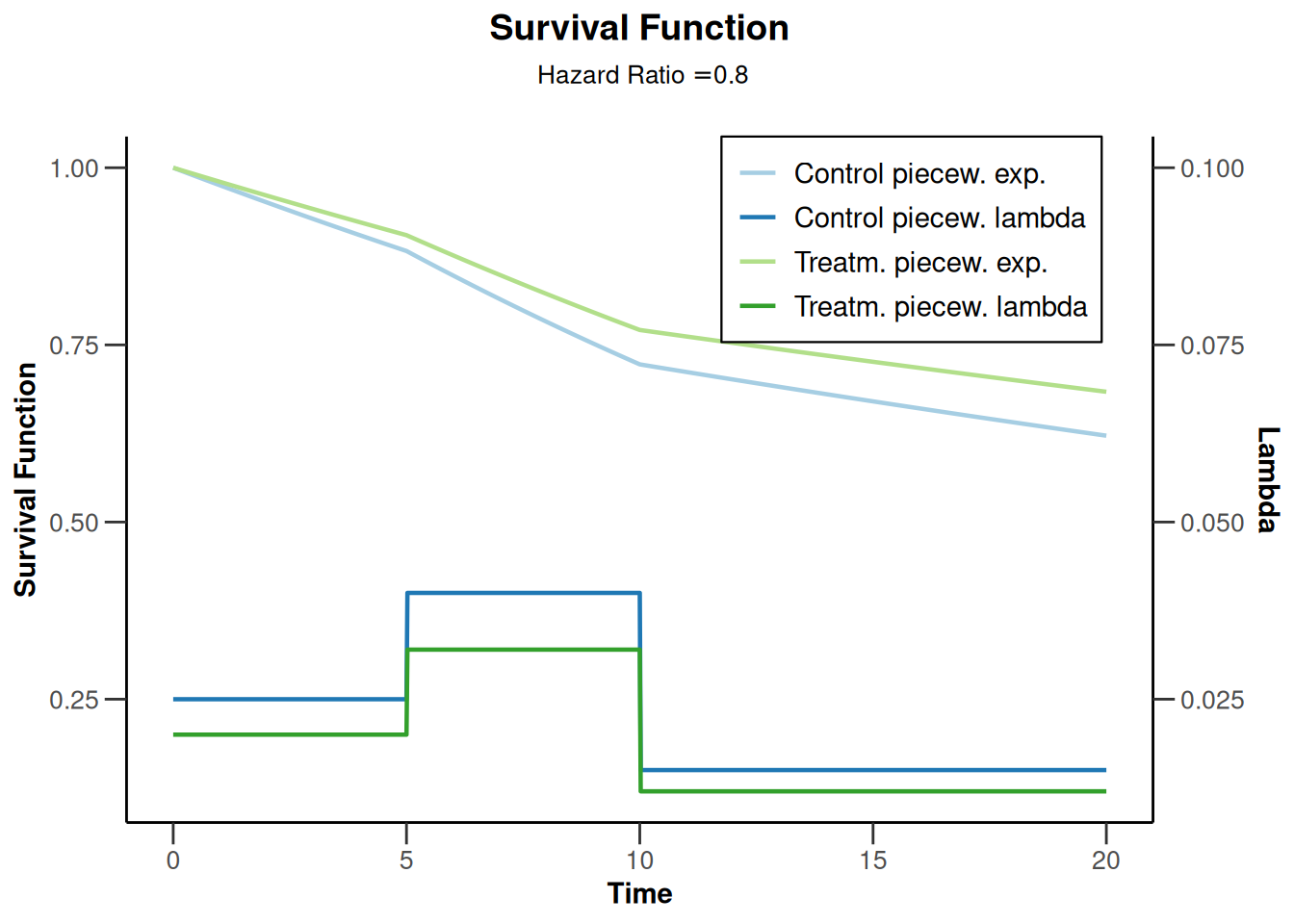

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

Warning in !is.null(lambda1) && !is.na(lambda1): 'length(x) = 5 > 1' in
coercion to 'logical(1)'

Power survival for one lambda

powerSurvival4 <- getPowerSurvival(
    accrualTime = 12,
    lambda2 = 0.04,
    hazardRatio = 0.6,
    maxNumberOfSubjects = 1400,
    maxNumberOfEvents = 300
)

plot(powerSurvival4, type = 13, legendPosition = 1)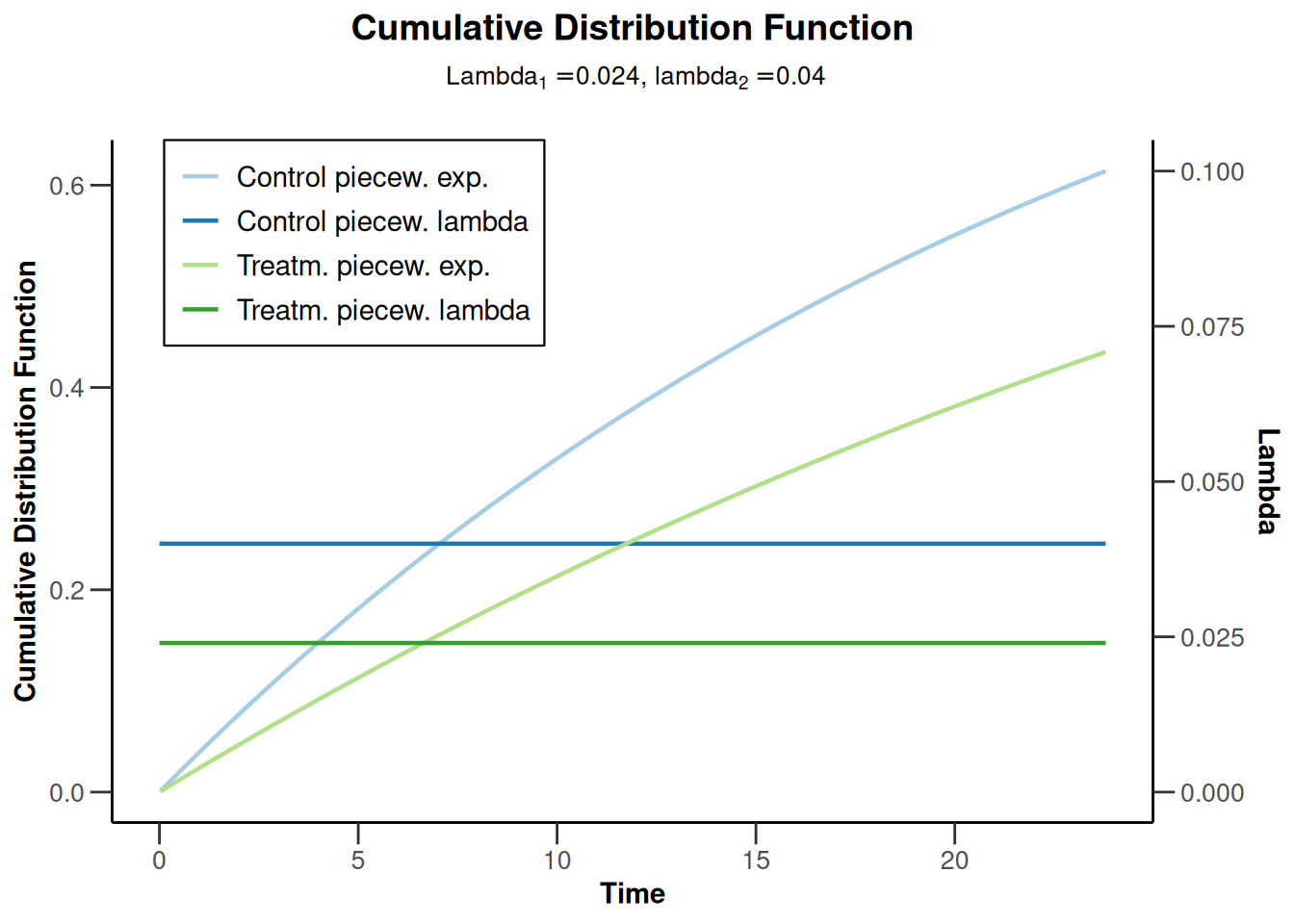

plot(powerSurvival4, type = 14, legendPosition = 5)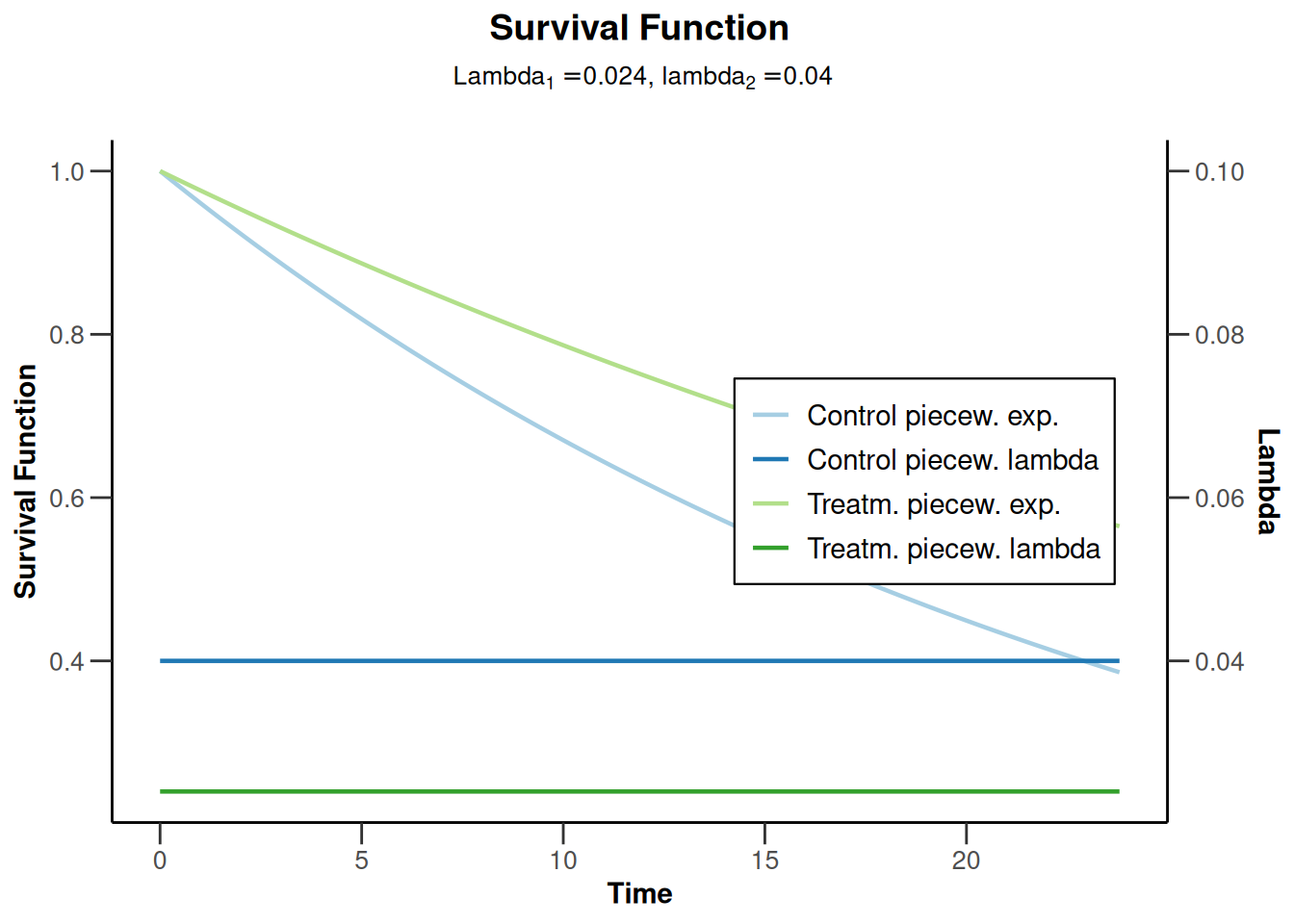

Power survival for default pi1 and pi2

powerSurvival5 <- getPowerSurvival(
    maxNumberOfSubjects = 1400,
    maxNumberOfEvents = 300
)

plot(powerSurvival5, type = 13, legendPosition = 1)

Warning: Only the first 'pi1' (0.2) was used for plotting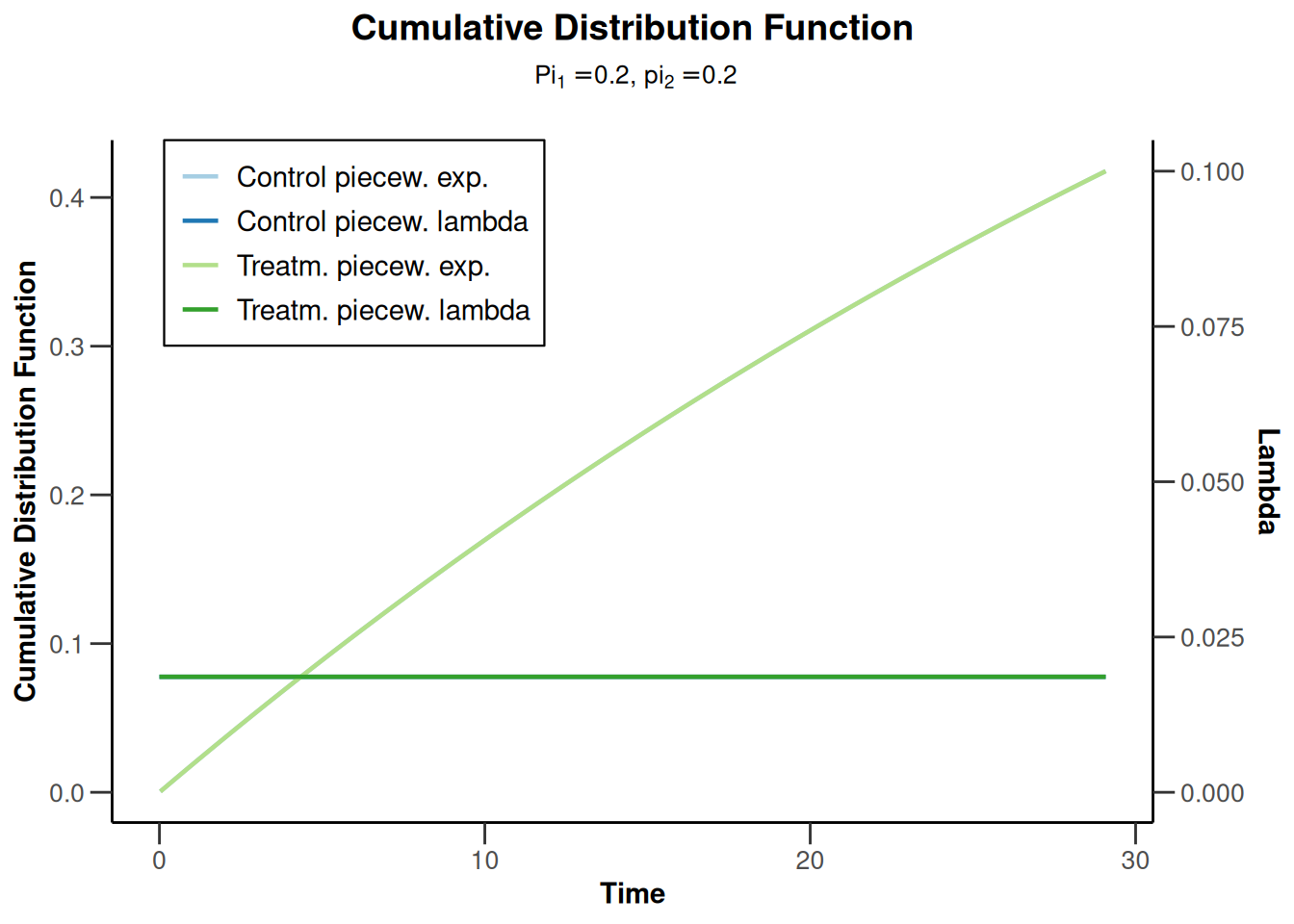

Warning in !is.na(designPlan$pi1) && !is.na(designPlan$pi2): 'length(x) = 4 >
1' in coercion to 'logical(1)'

plot(powerSurvival5, type = 14, legendPosition = 5)

Warning: Only the first 'pi1' (0.2) was used for plotting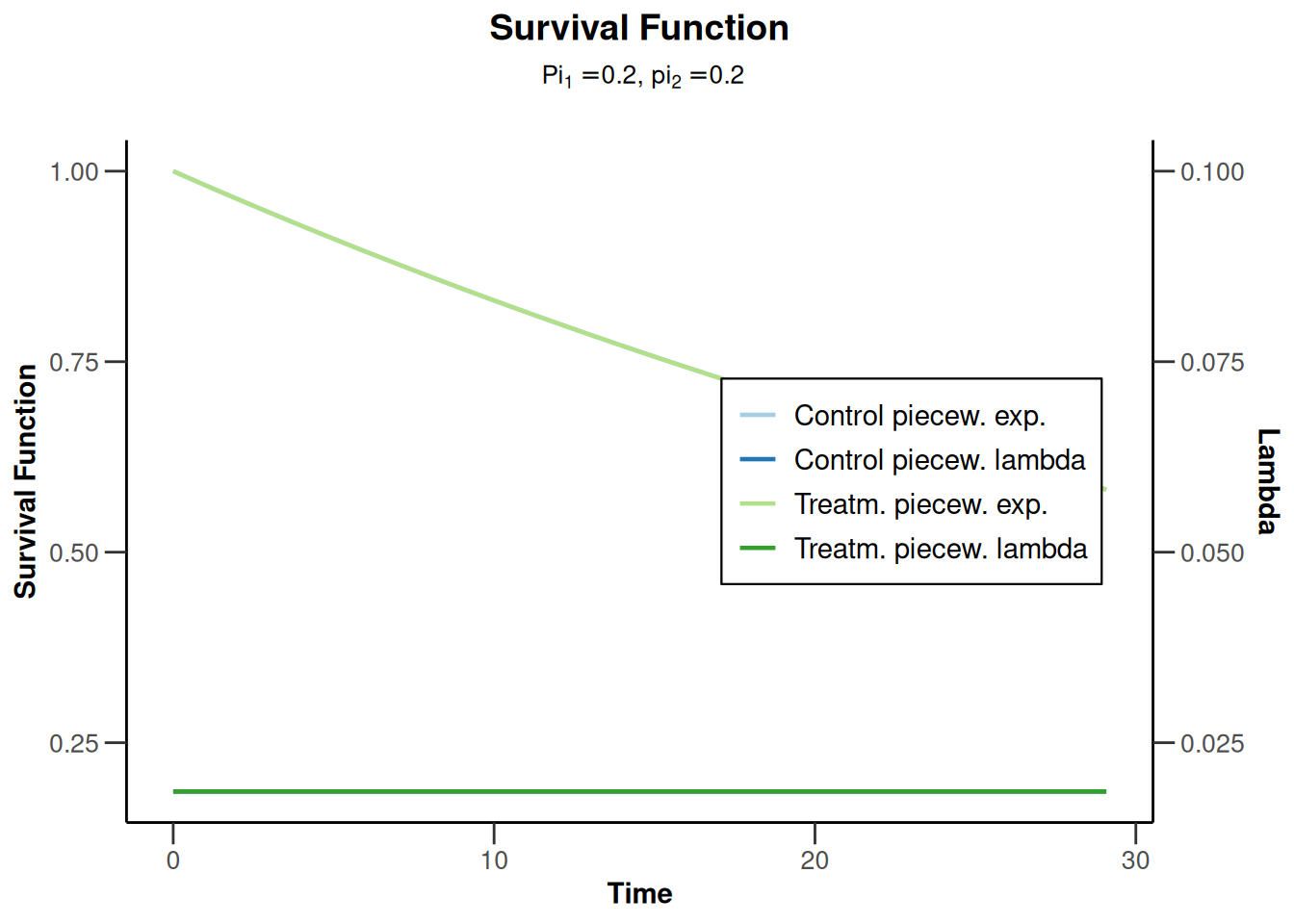

Warning: 'length(x) = 4 > 1' in coercion to 'logical(1)'

Simulation plots

Simulation means (continuous endpoint)

simulationResults1 <- getSimulationMeans(
    design = getDesignFisher(kMax = 2),
    plannedSubjects = c(20, 40), maxNumberOfIterations = 1000,
    seed = 12345
)

plot(simulationResults1, type = "all", grid = 0)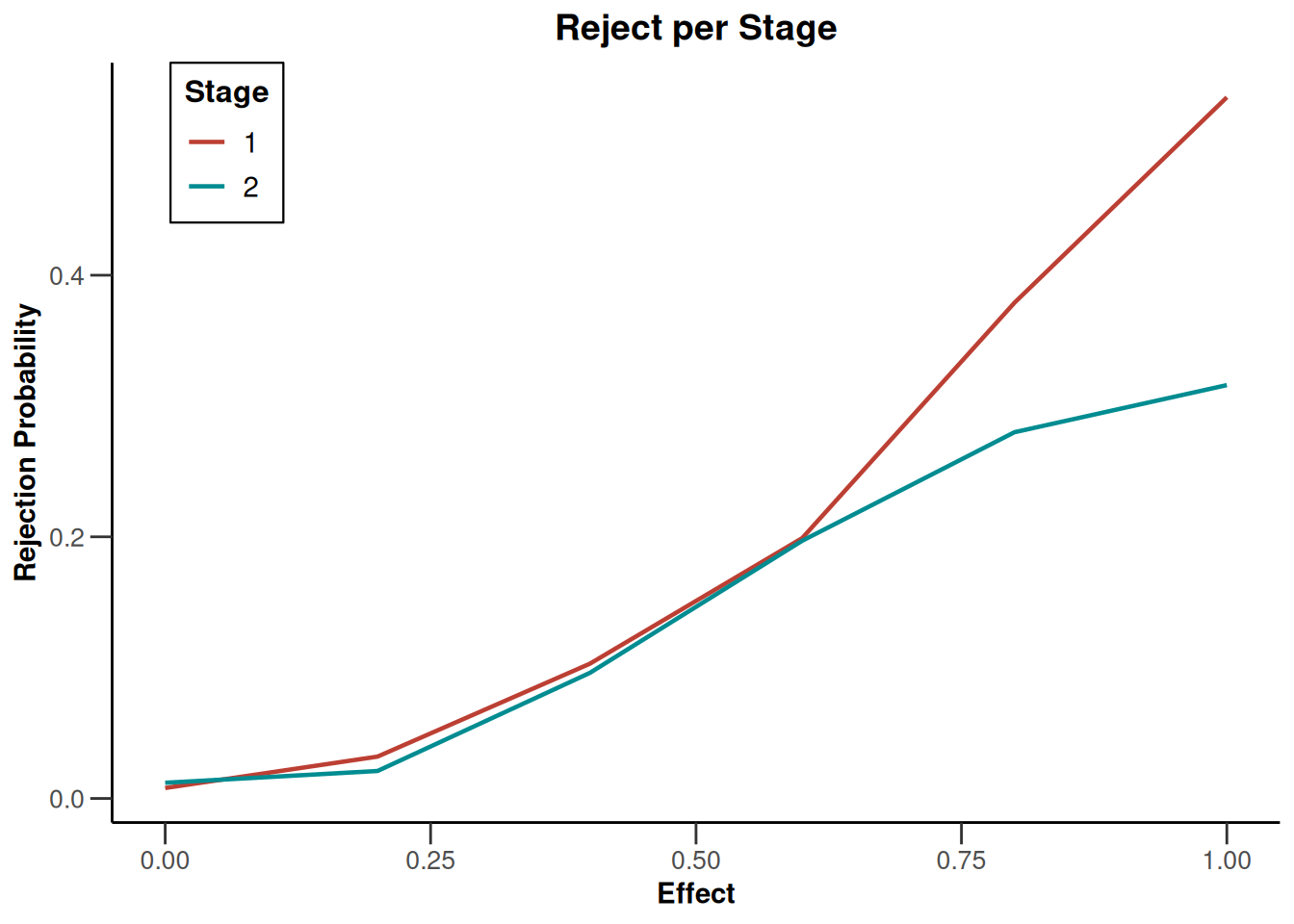

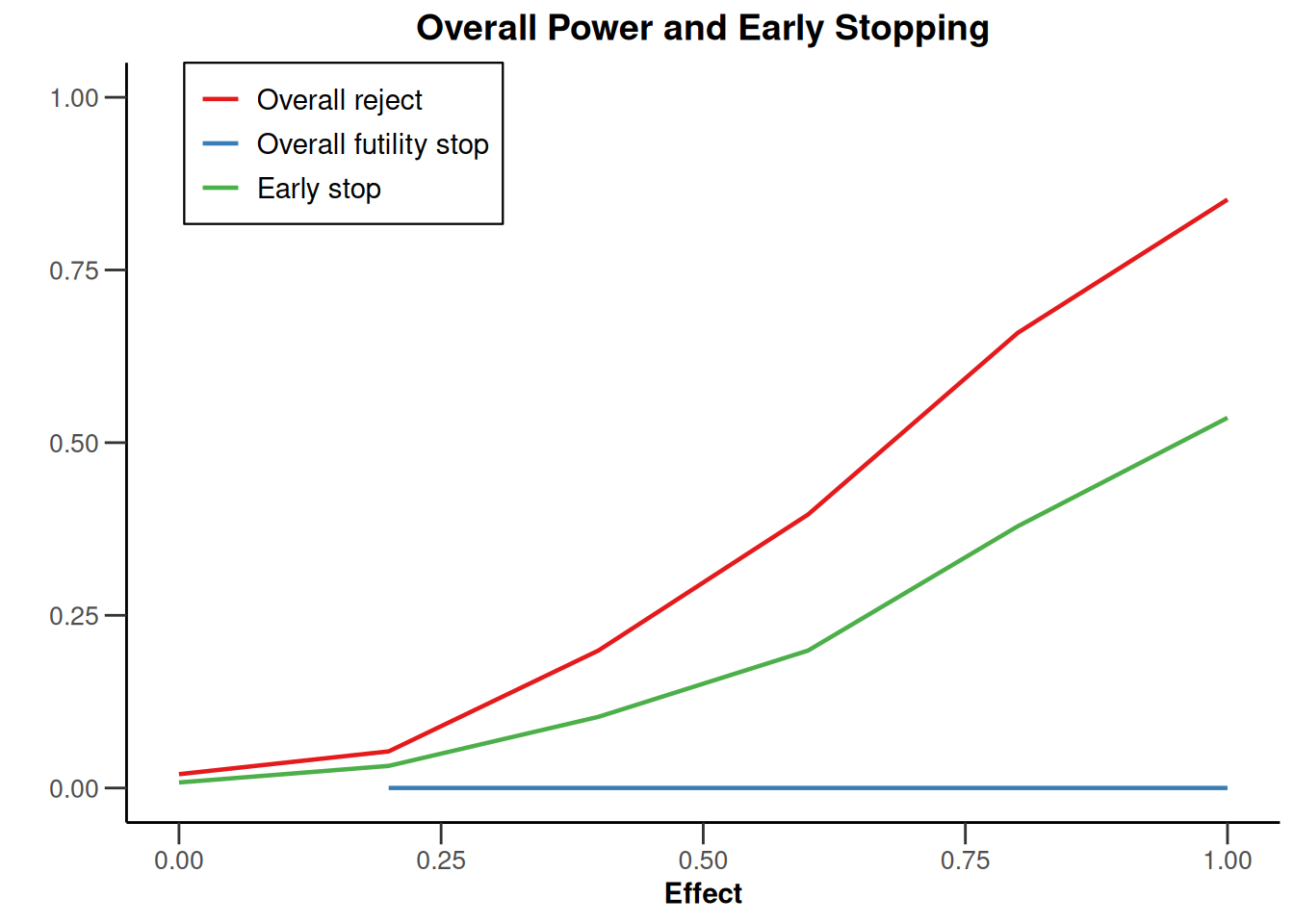
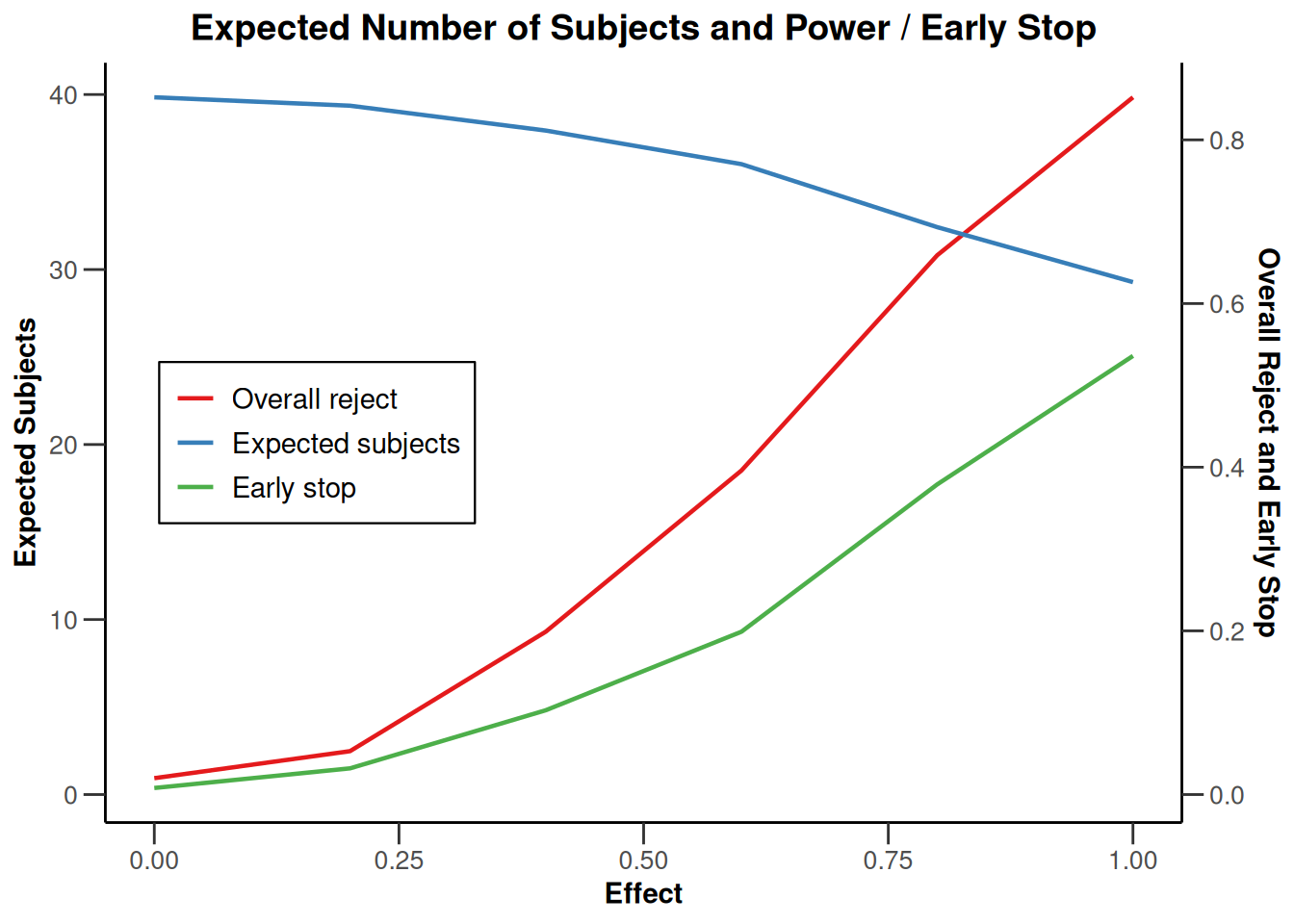
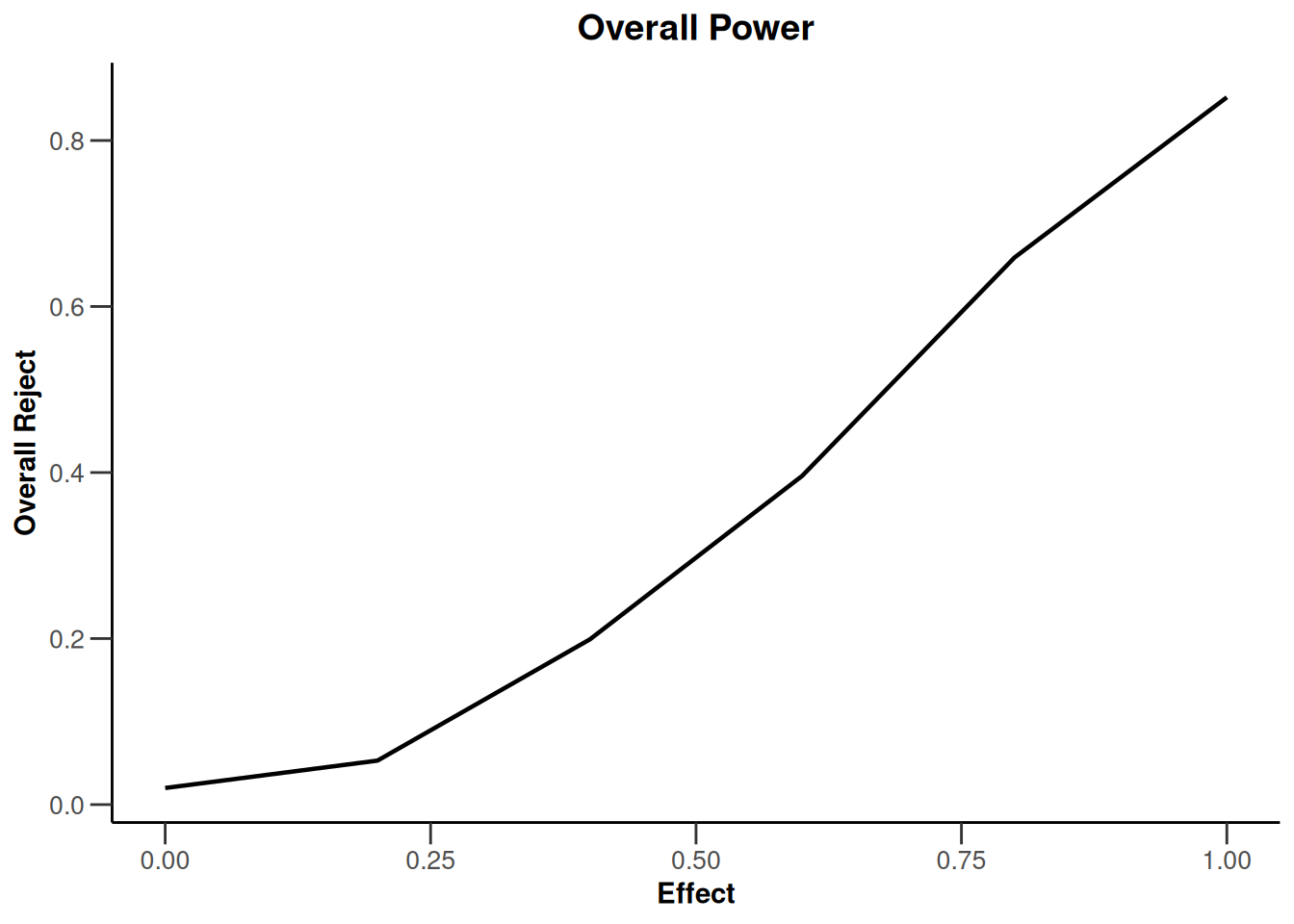
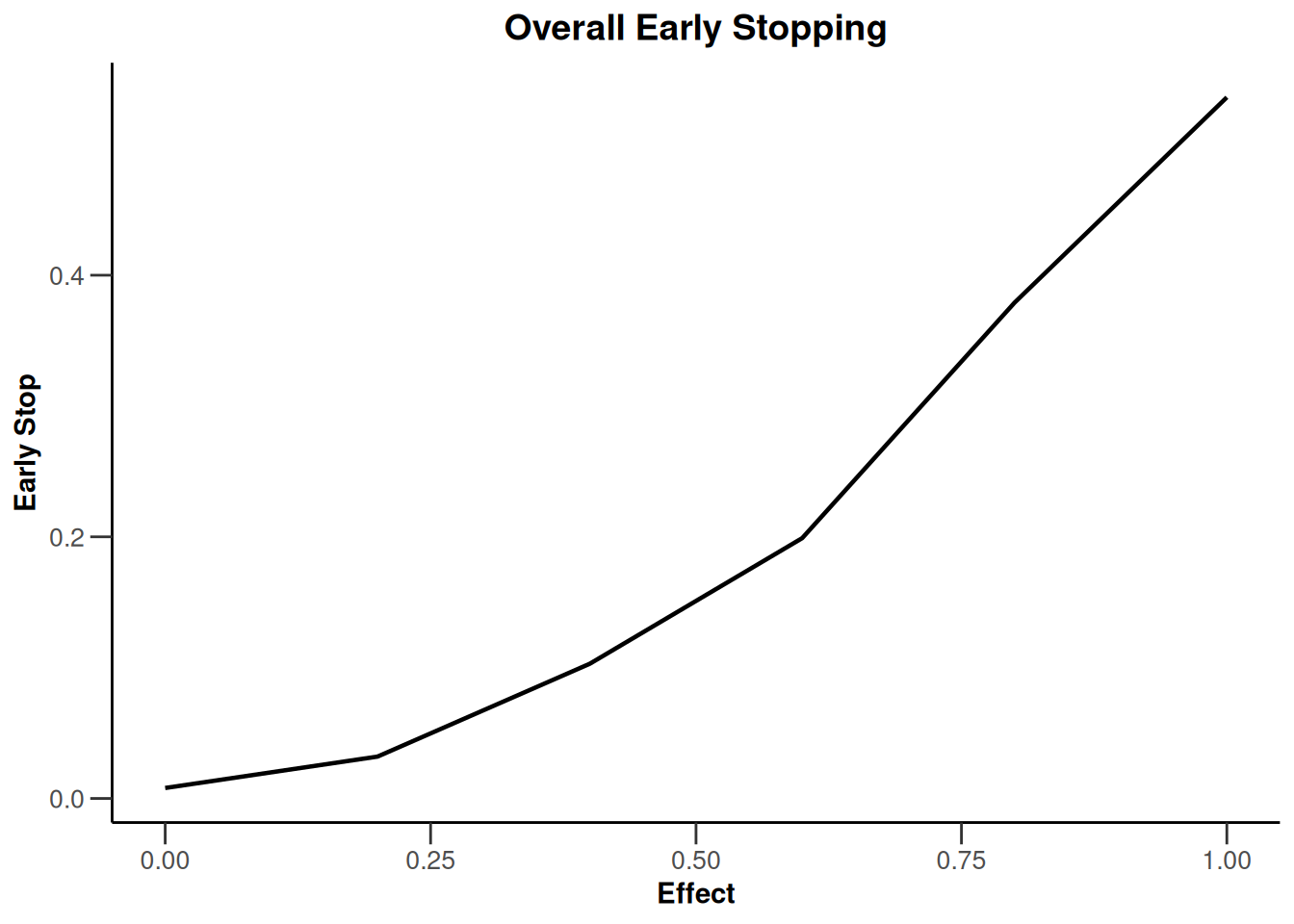
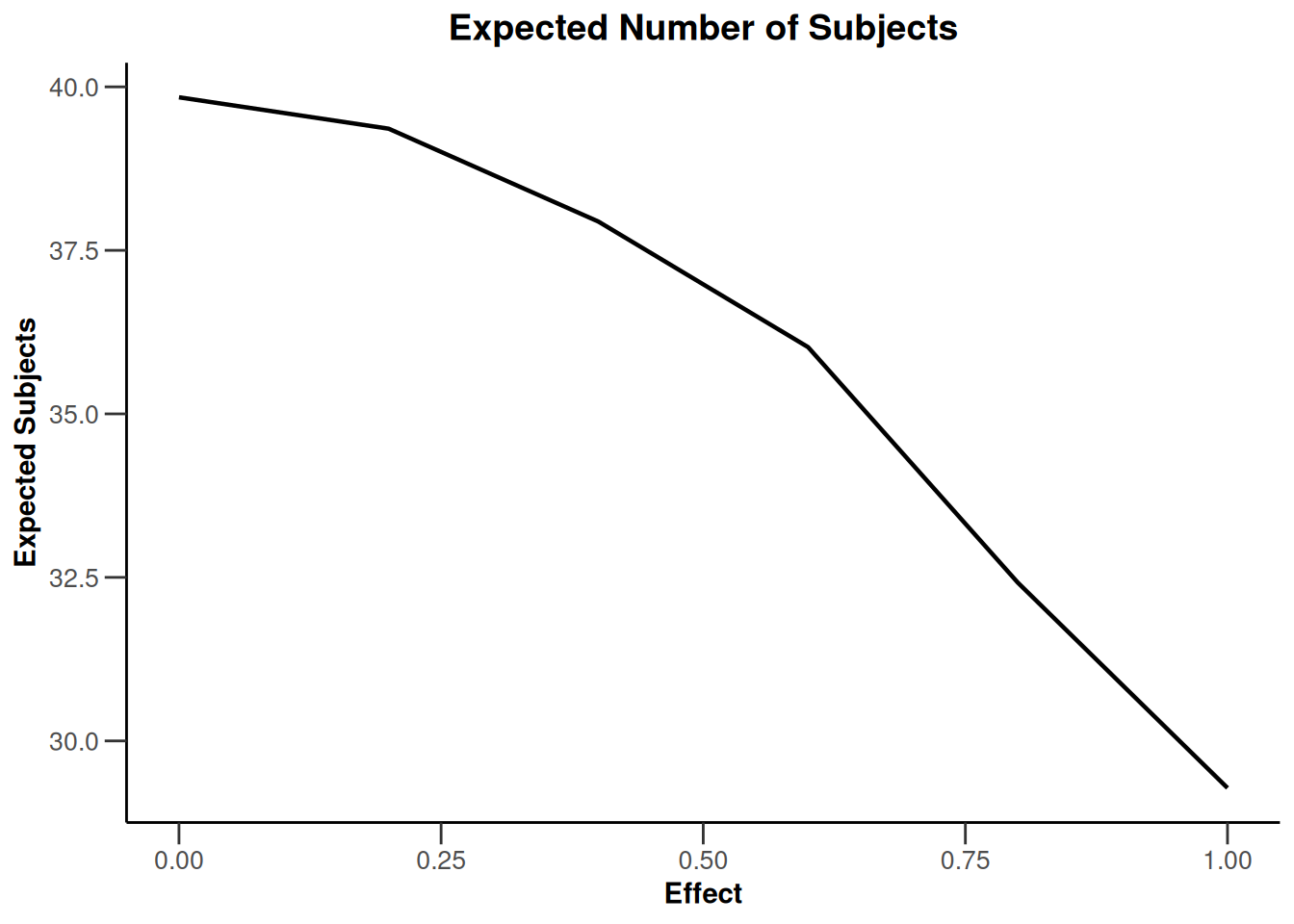
plot(simulationResults1, type = 4)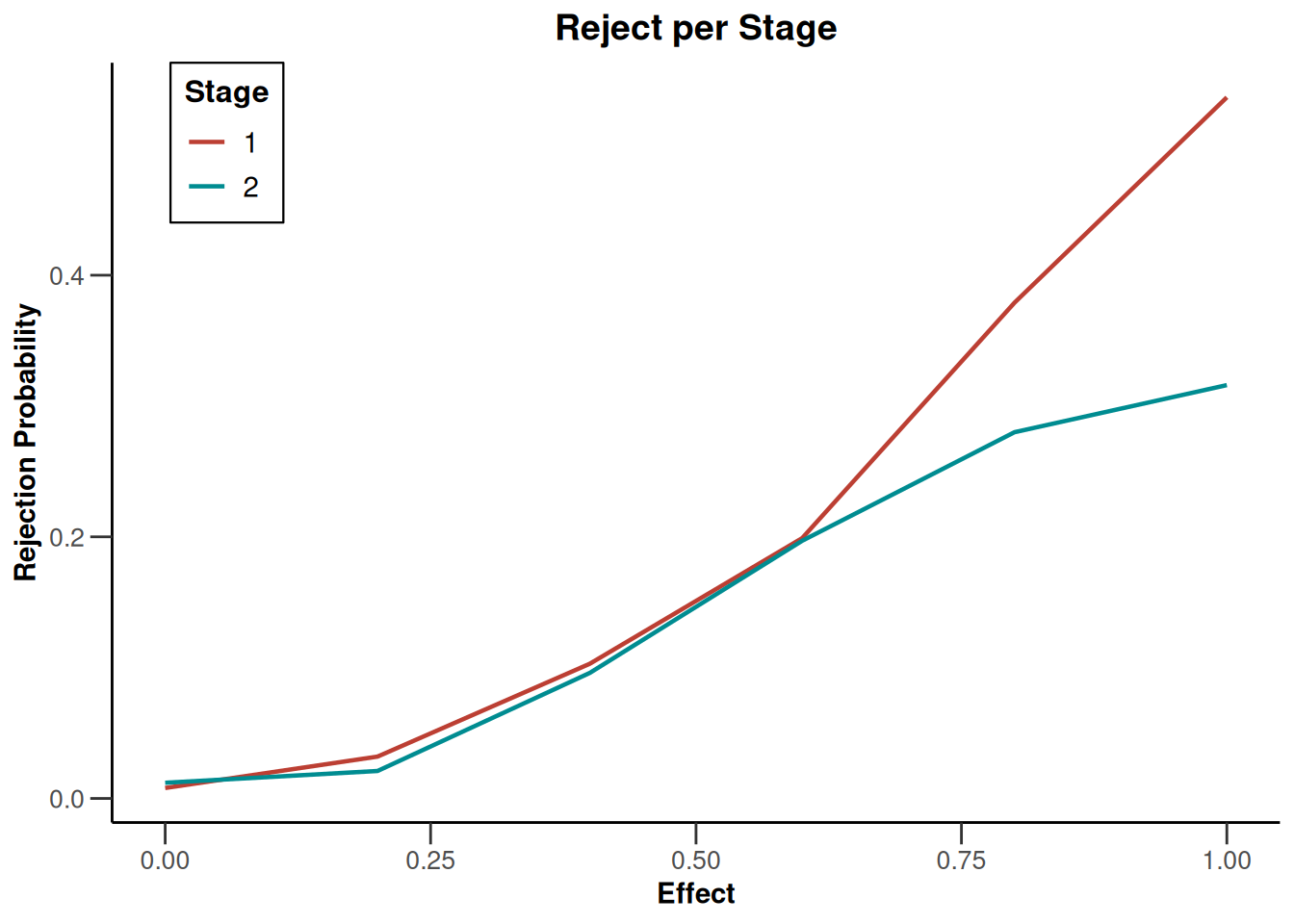

plot(simulationResults1, type = 5)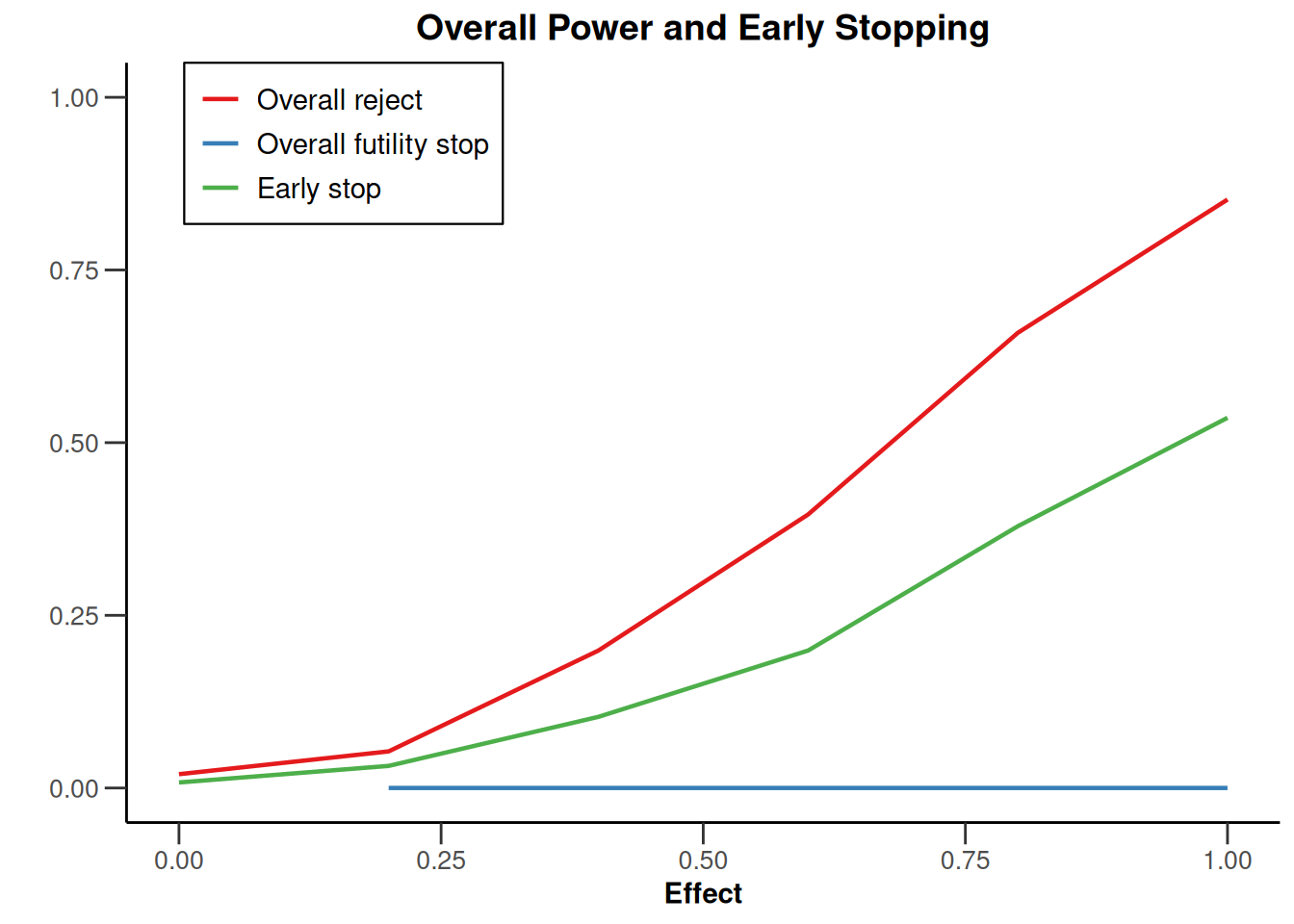

plot(simulationResults1, type = 6)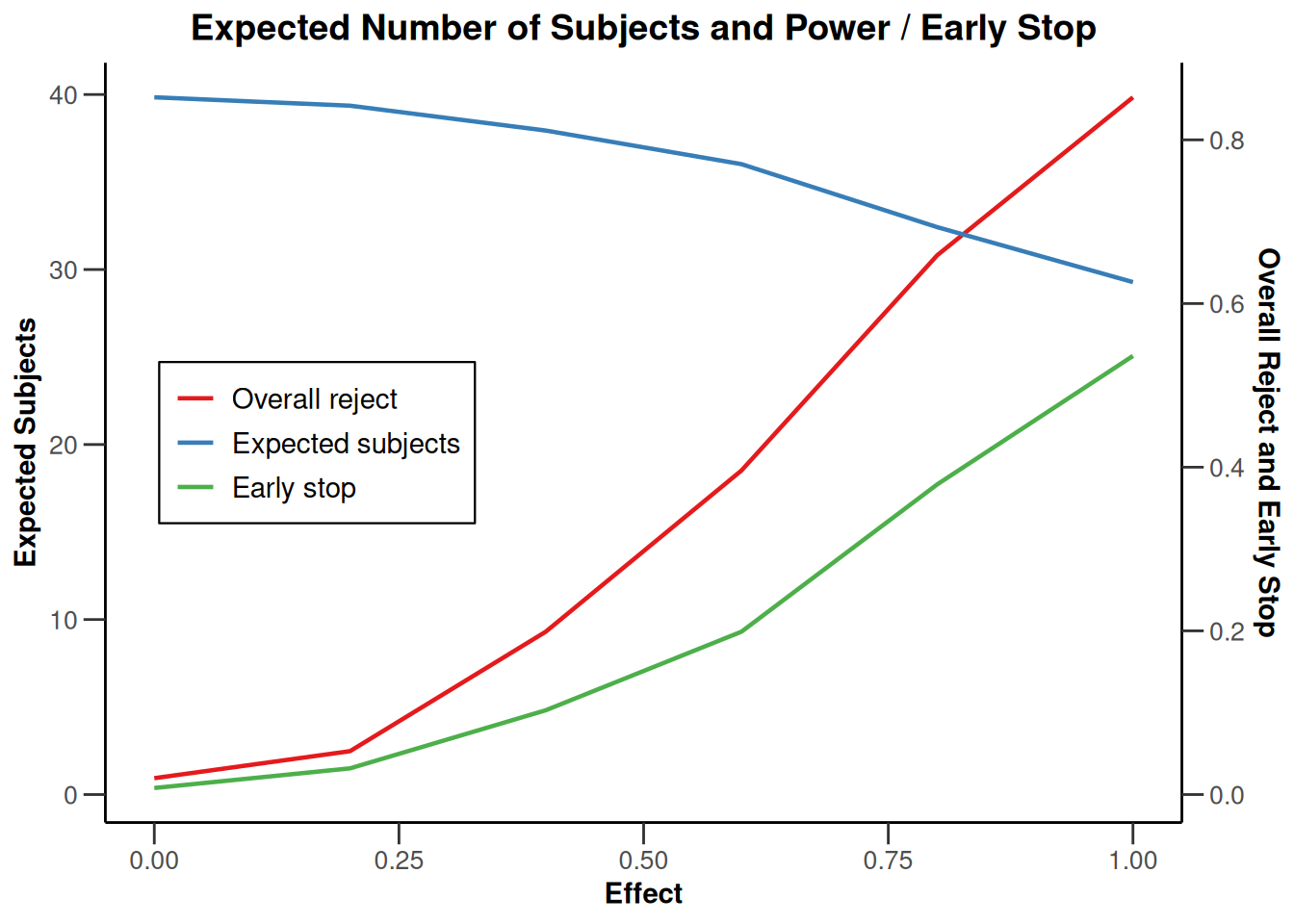

Simulation rates (binary endpoint)

simulationResults1 <- getSimulationRates(
    design = getDesignFisher(kMax = 2),
    plannedSubjects = c(20, 40), maxNumberOfIterations = 1000,
    seed = 12345
)

plot(simulationResults1, type = 4)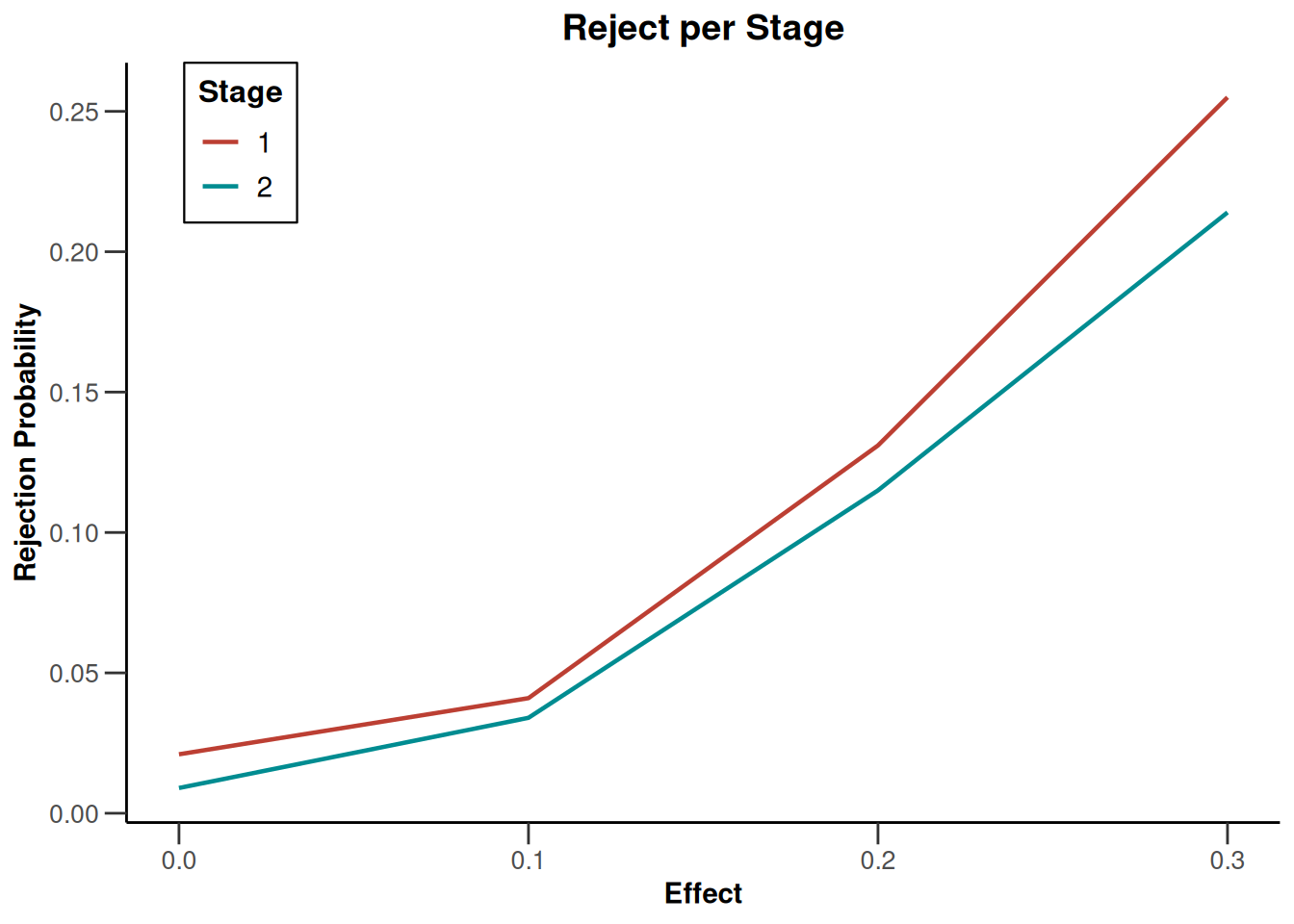

plot(simulationResults1, type = 5)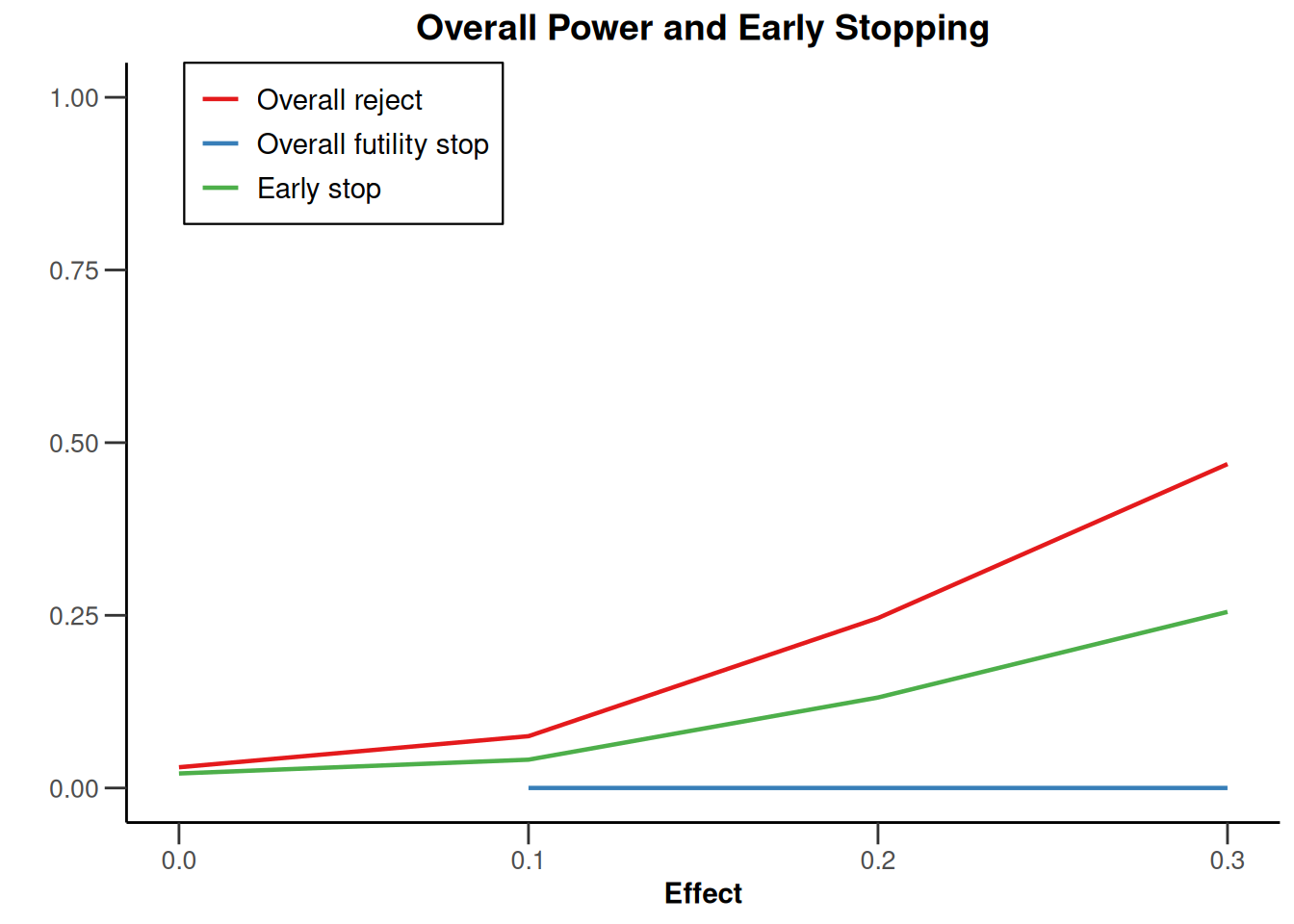

plot(simulationResults1, type = 6)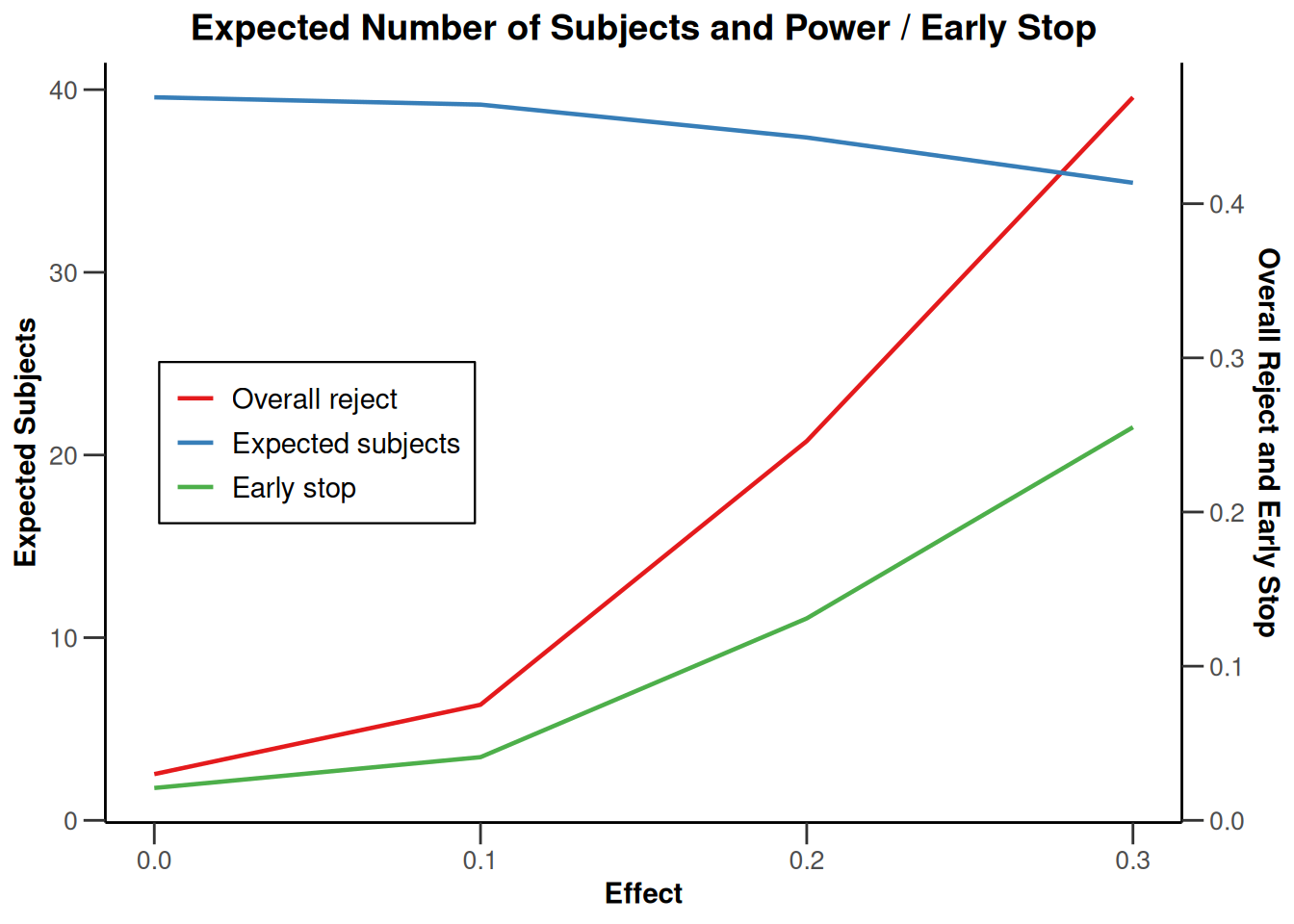

Simulation plots survival (survival endpoint)

simulationResults1 <- getSimulationSurvival(
    accrualTime = 12,
    maxNumberOfSubjects = 1405,
    plannedEvents = 300, maxNumberOfIterations = 1000,
    seed = 12345
)

plot(simulationResults1, type = 5)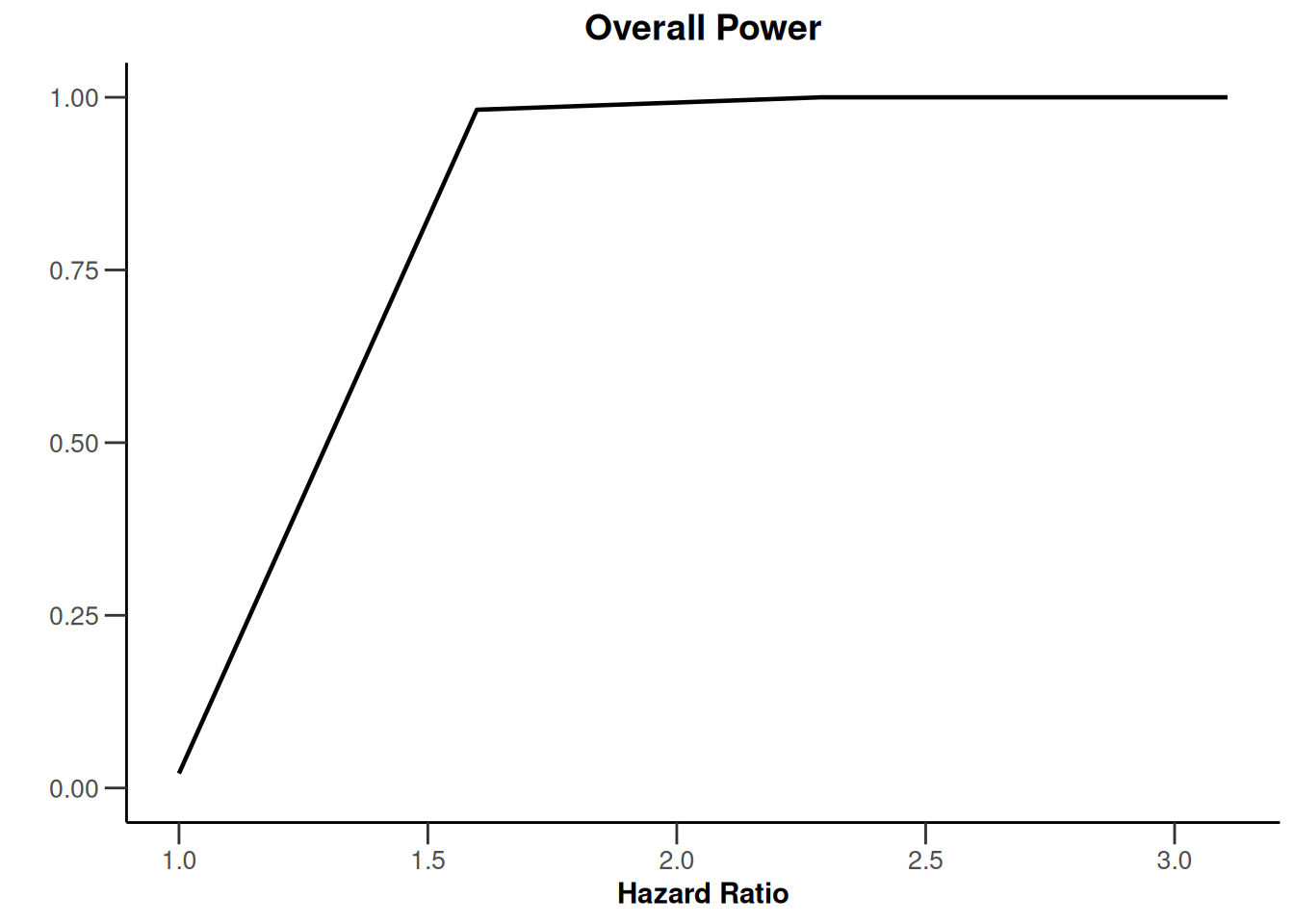

plot(simulationResults1, type = 6)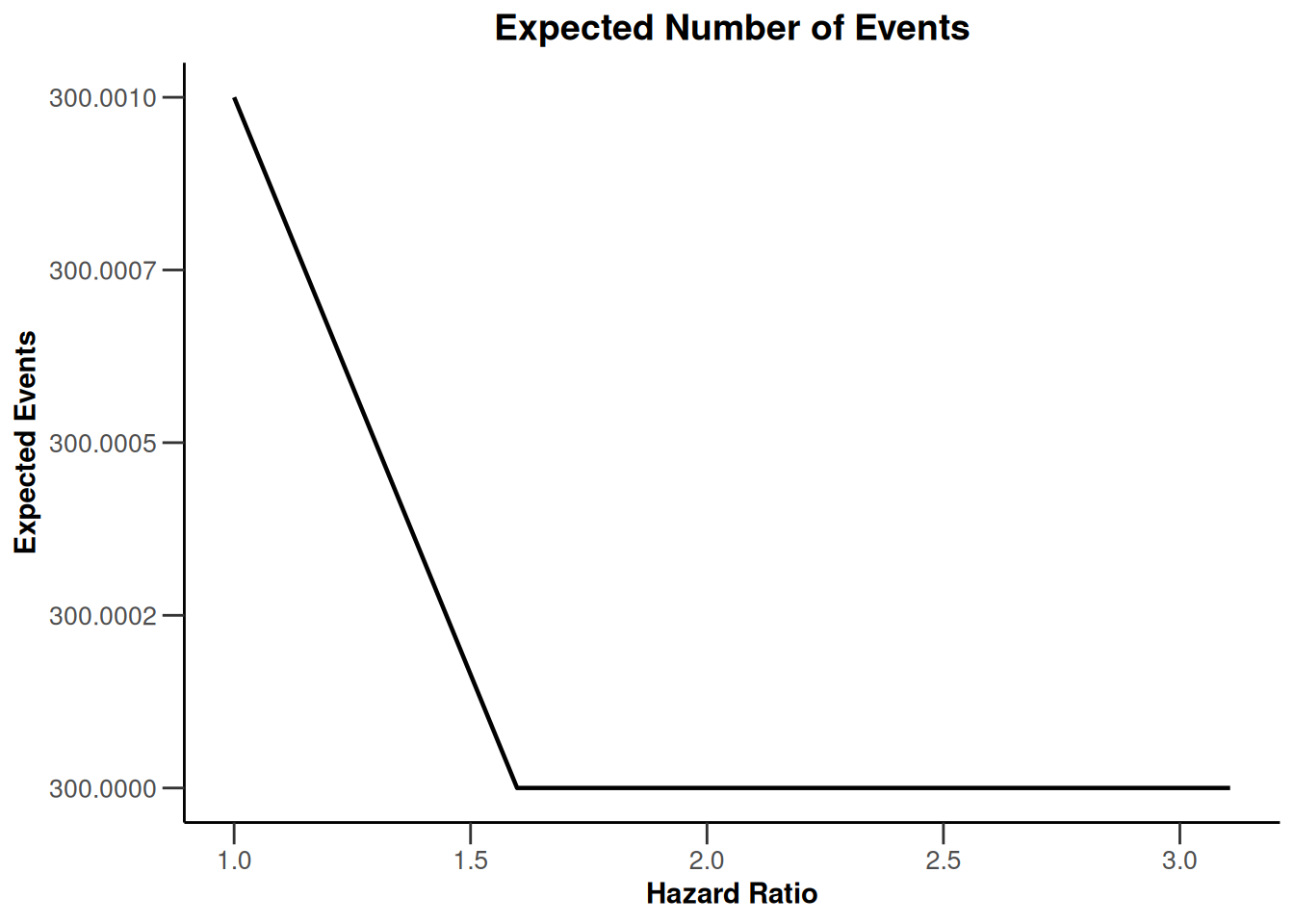

plot(simulationResults1, type = 7)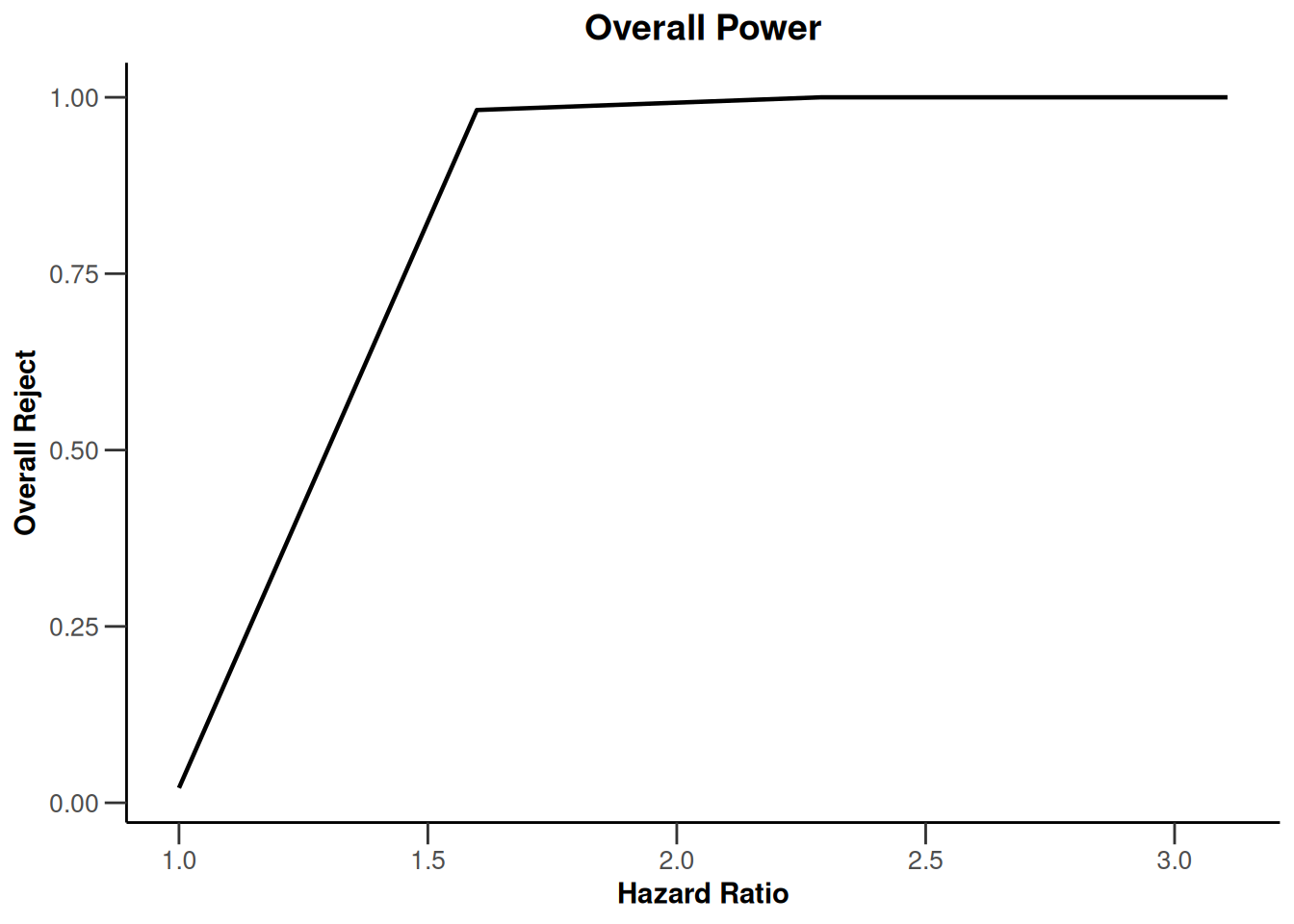

plot(simulationResults1, type = 9)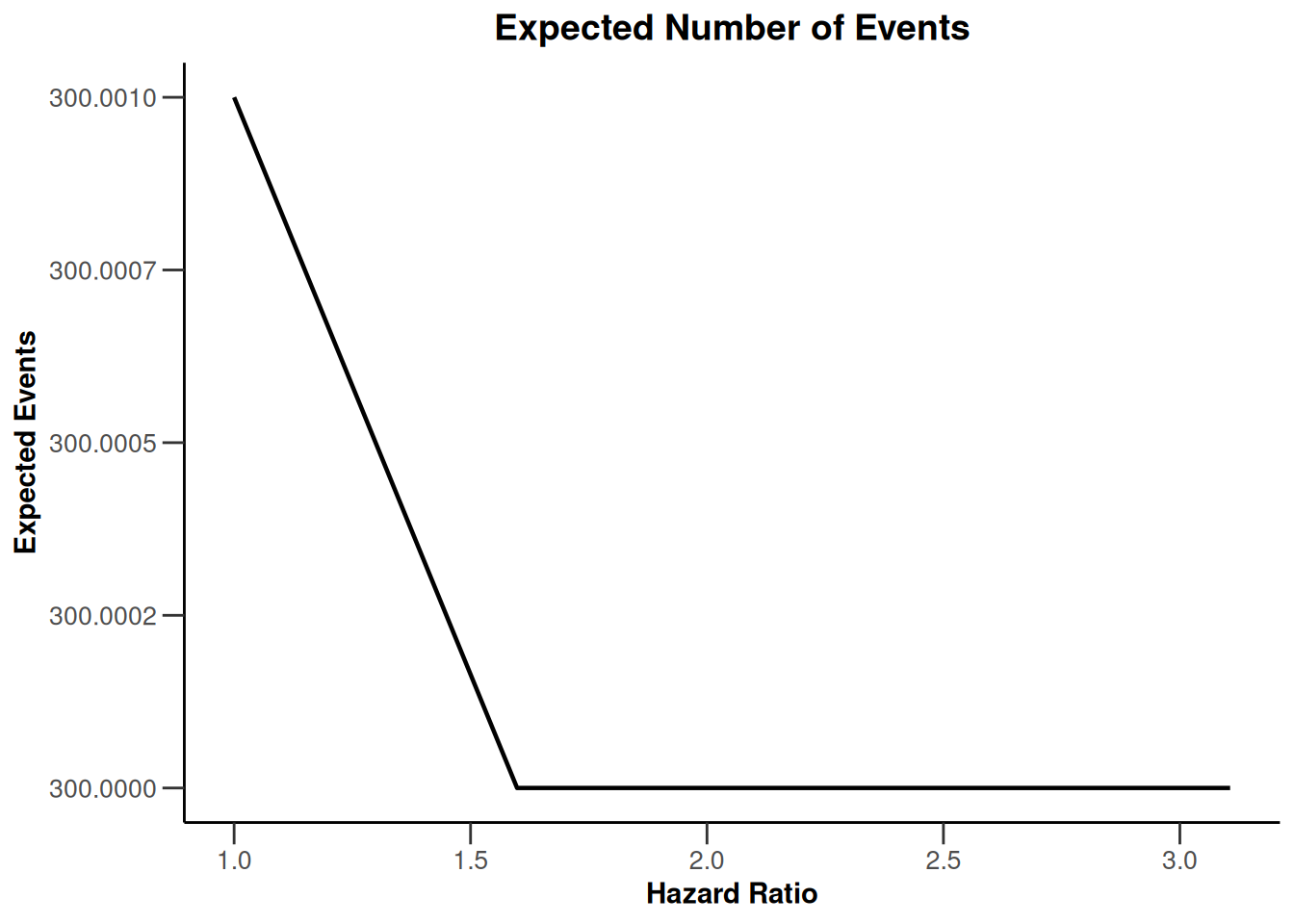

plot(simulationResults1, type = 10)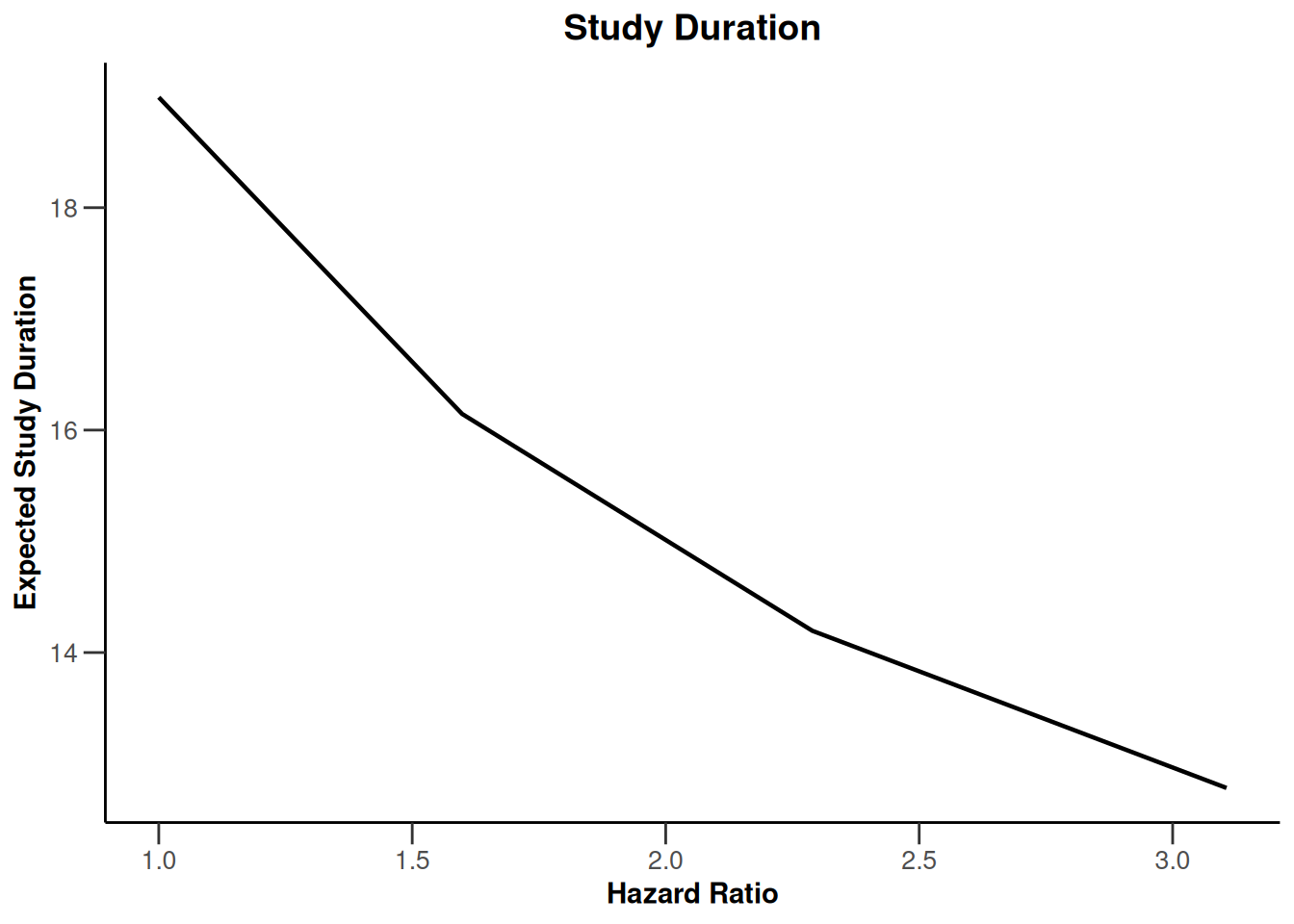

plot(simulationResults1, type = 11)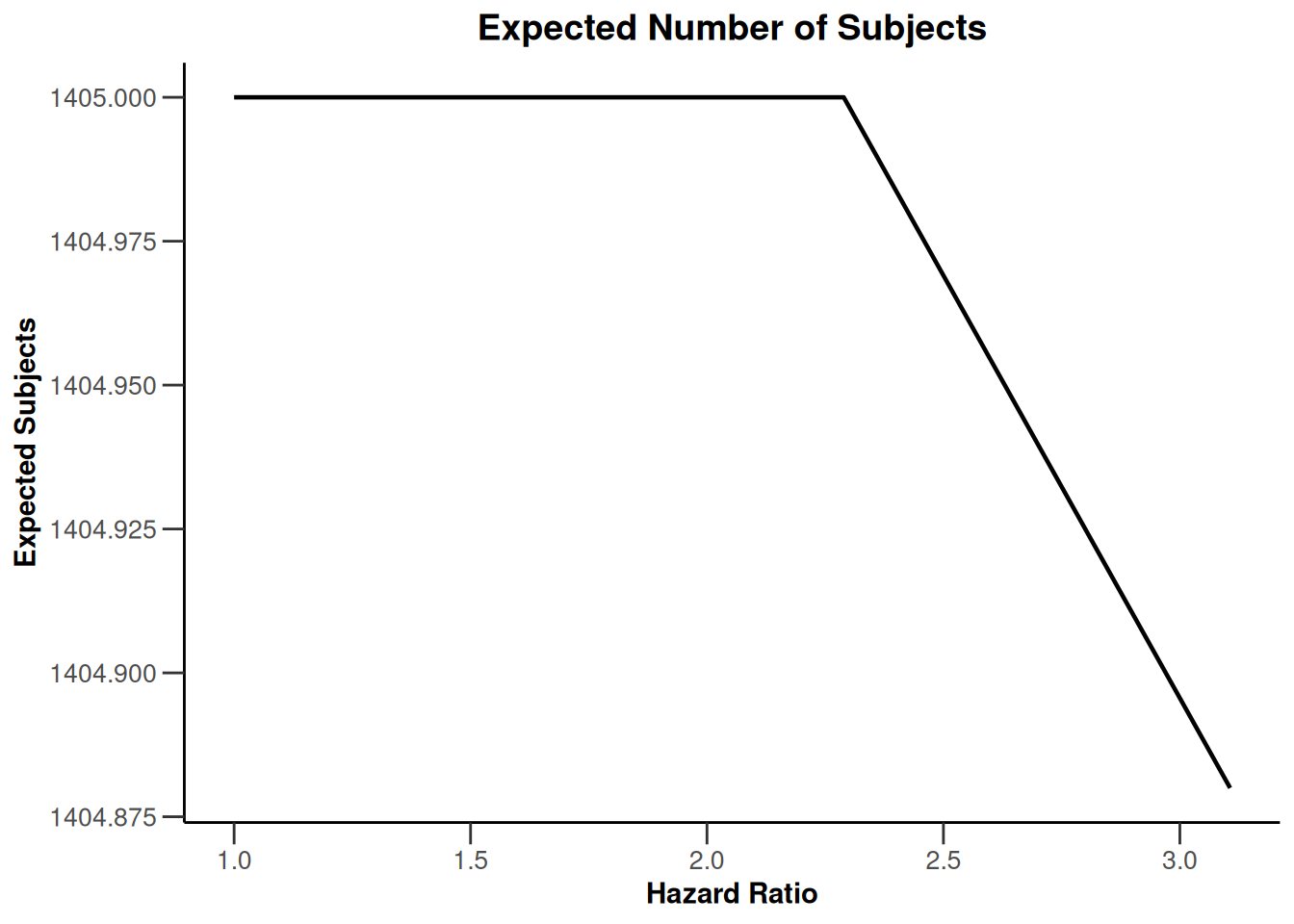

plot(simulationResults1, type = 12)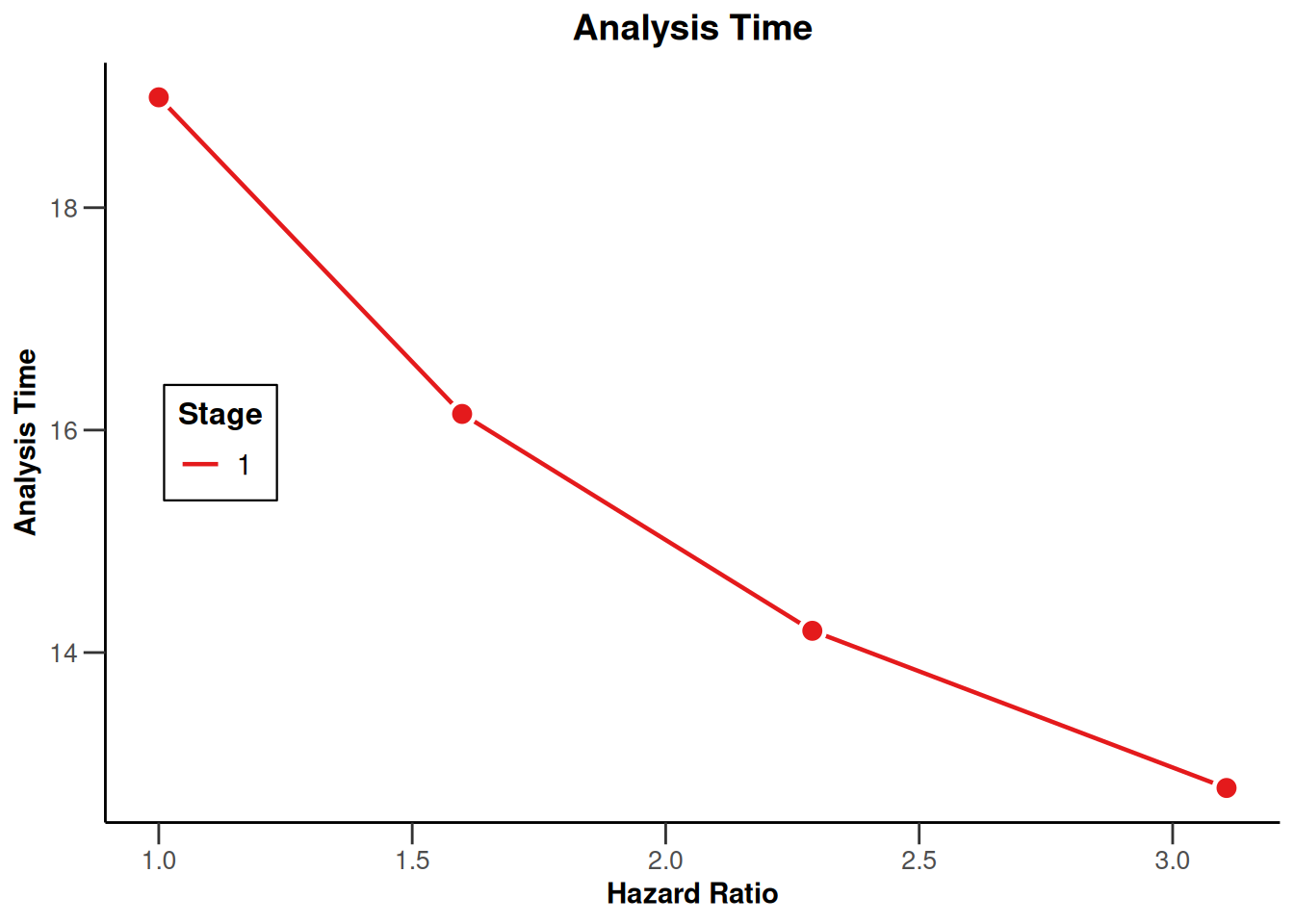

plot(simulationResults1, type = 13)

Warning: Only the first 'pi1' (0.2) was used for plotting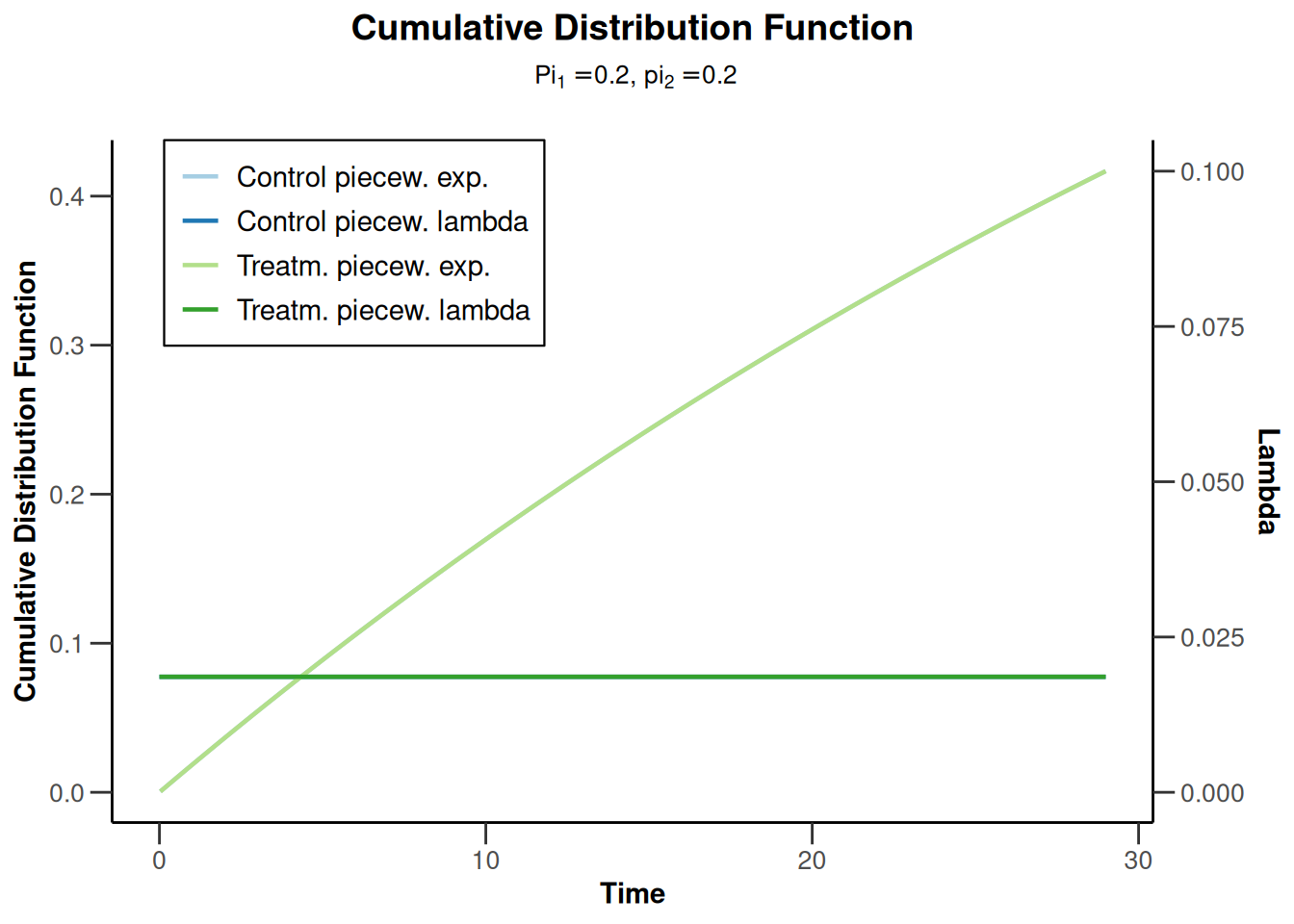

Warning in !is.na(designPlan$pi1) && !is.na(designPlan$pi2): 'length(x) = 4 >
1' in coercion to 'logical(1)'

plot(simulationResults1, type = 14)

Warning: Only the first 'pi1' (0.2) was used for plotting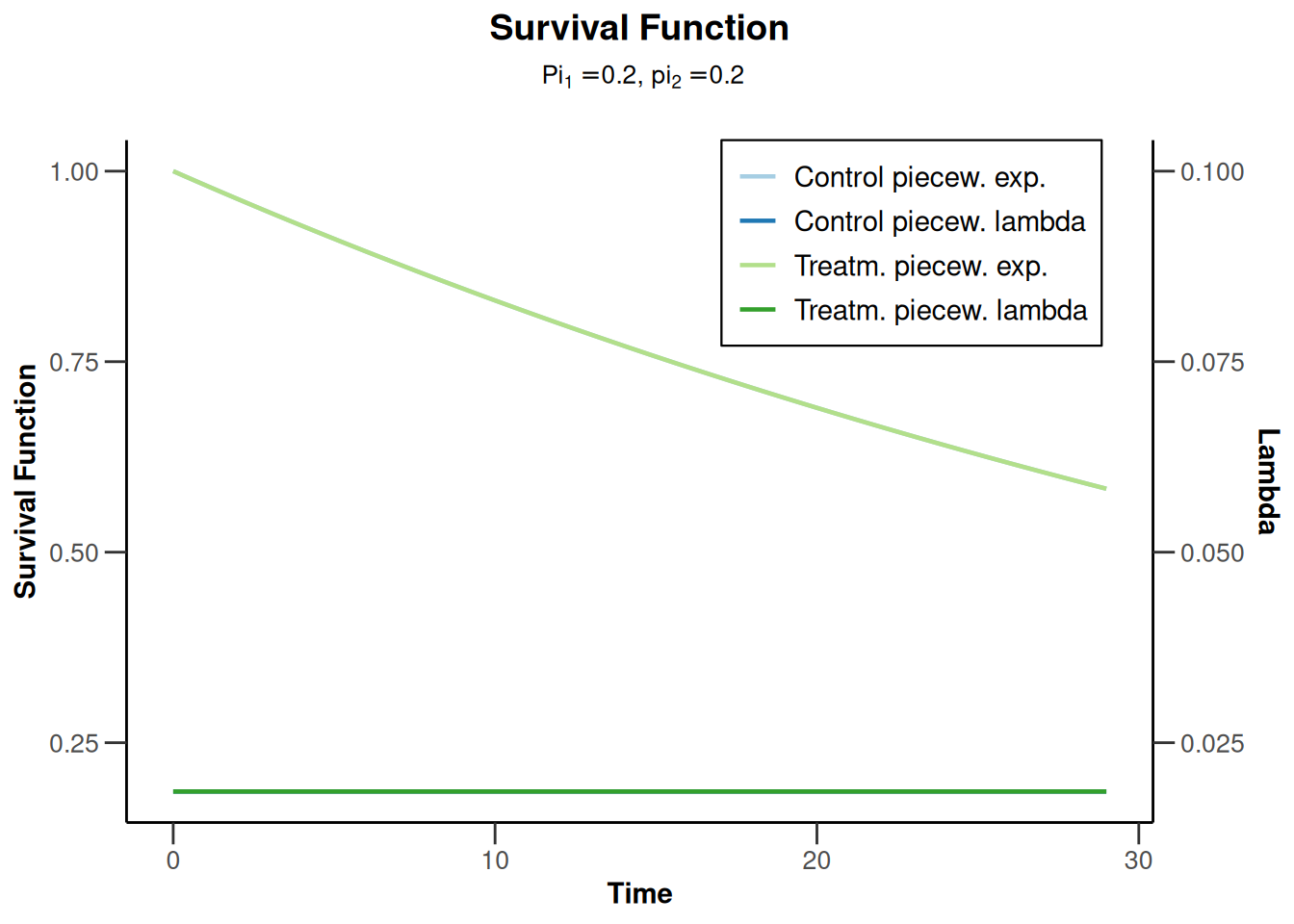

Warning: 'length(x) = 4 > 1' in coercion to 'logical(1)'

simulationResults2 <- getSimulationSurvival(
    accrualTime = 12,
    lambda2 = 0.03,
    hazardRatio = 0.8,
    maxNumberOfSubjects = 1405,
    plannedEvents = 300, maxNumberOfIterations = 1000,
    seed = 23456
)

plot(simulationResults2, type = 13)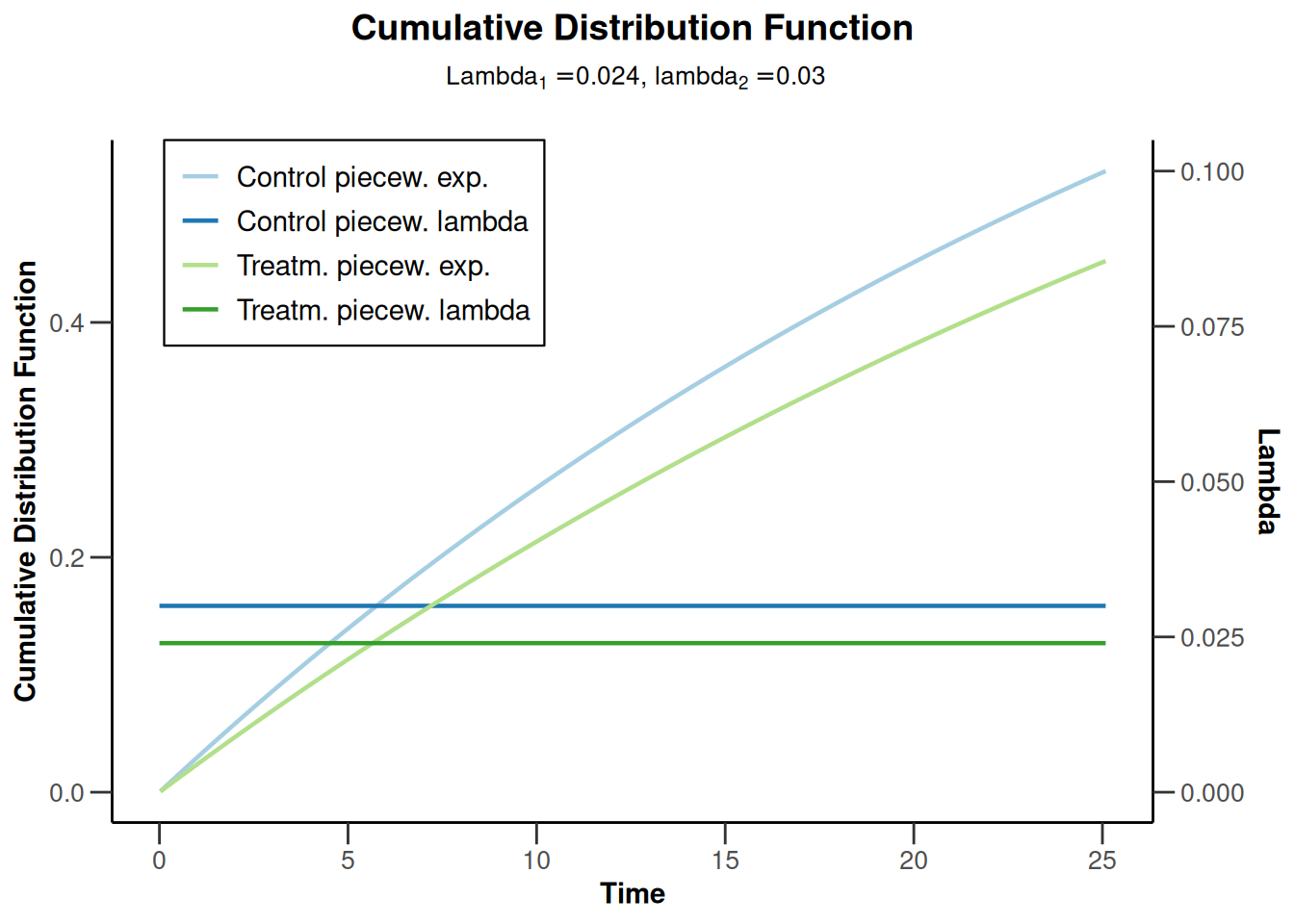

plot(simulationResults2, type = 14)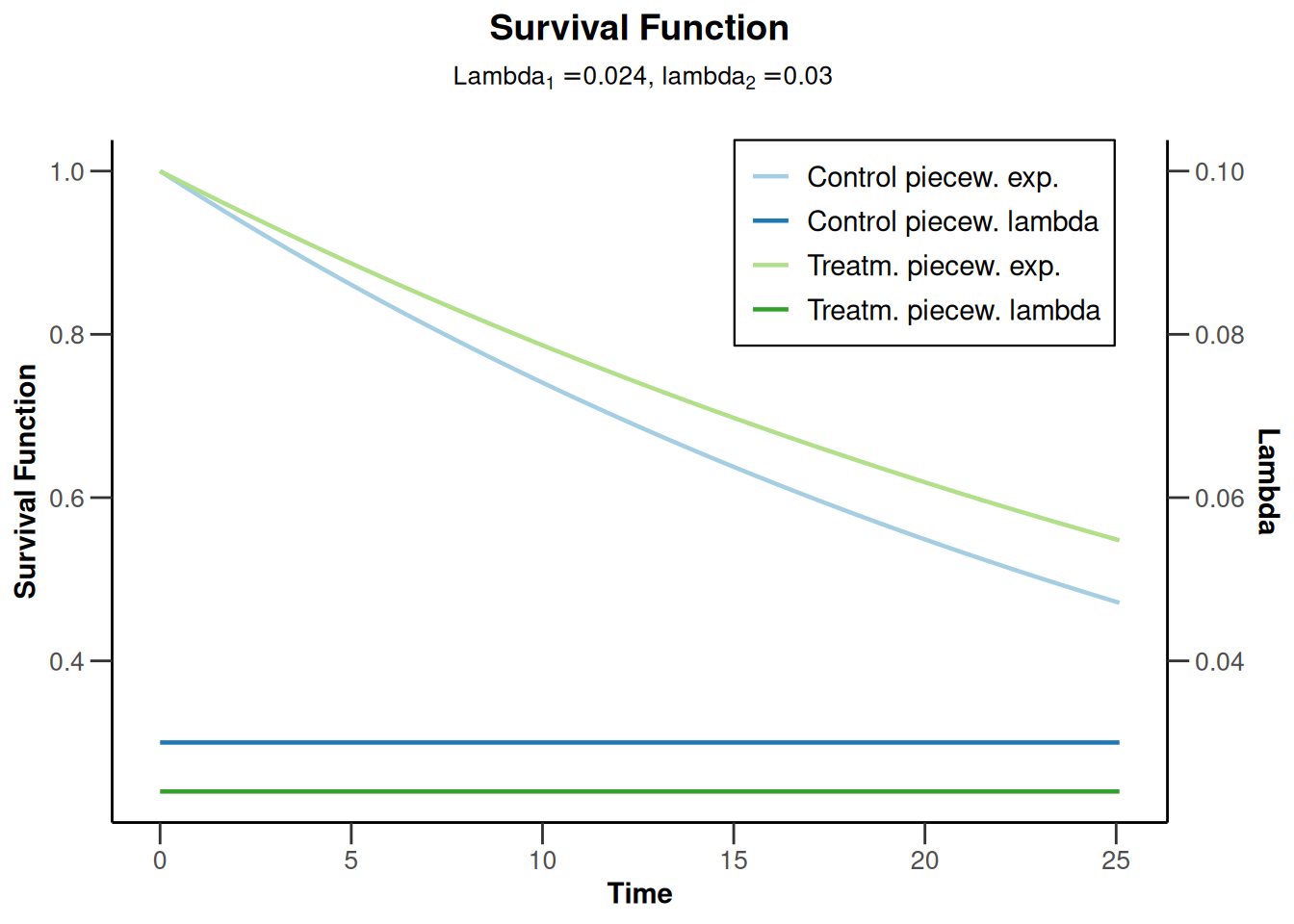

System: rpact 3.3.4, R version 4.2.2 (2022-10-31 ucrt), platform: x86_64-w64-mingw32

To cite R in publications use:

R Core Team (2022). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

To cite package ‘rpact’ in publications use:

Wassmer G, Pahlke F (2023). rpact: Confirmatory Adaptive Clinical Trial Design and Analysis. https://www.rpact.org, https://www.rpact.com, https://github.com/rpact-com/rpact.

Reuse

https://creativecommons.org/licenses/by-sa/4.0/