library(rpact)
packageVersion("rpact") # version should be version 3.0 or laterHow to Create One- and Multi-Arm Analysis Result Plots with rpact
Utilities
Preparation
First, load the rpact package
[1] '4.0.0'Create a design
designIN <- getDesignInverseNormal(
kMax = 4, alpha = 0.02,
futilityBounds = c(-0.5, 0, 0.5), bindingFutility = FALSE,
typeOfDesign = "asKD", gammaA = 1.2,
informationRates = c(0.15, 0.4, 0.7, 1)
)
designF <- getDesignFisher(
kMax = 4, alpha = 0.02,
informationRates = c(0.15, 0.4, 0.7, 1)
)Analysis results base
Analysis results base - means
simpleDataExampleMeans1 <- getDataset(
n = c(120, 130, 130),
means = c(0.45, 0.51, 0.45) * 100,
stDevs = c(1.3, 1.4, 1.2) * 100
)
x <- getAnalysisResults(
design = designIN, dataInput = simpleDataExampleMeans1,
nPlanned = 130, thetaH0 = 30, thetaH1 = 60, assumedStDev = 100
)Calculation of final confidence interval performed for kMax = 4 (for kMax > 2, it is theoretically shown that it is valid only if no sample size change was performed)plot(x, thetaRange = c(10, 80))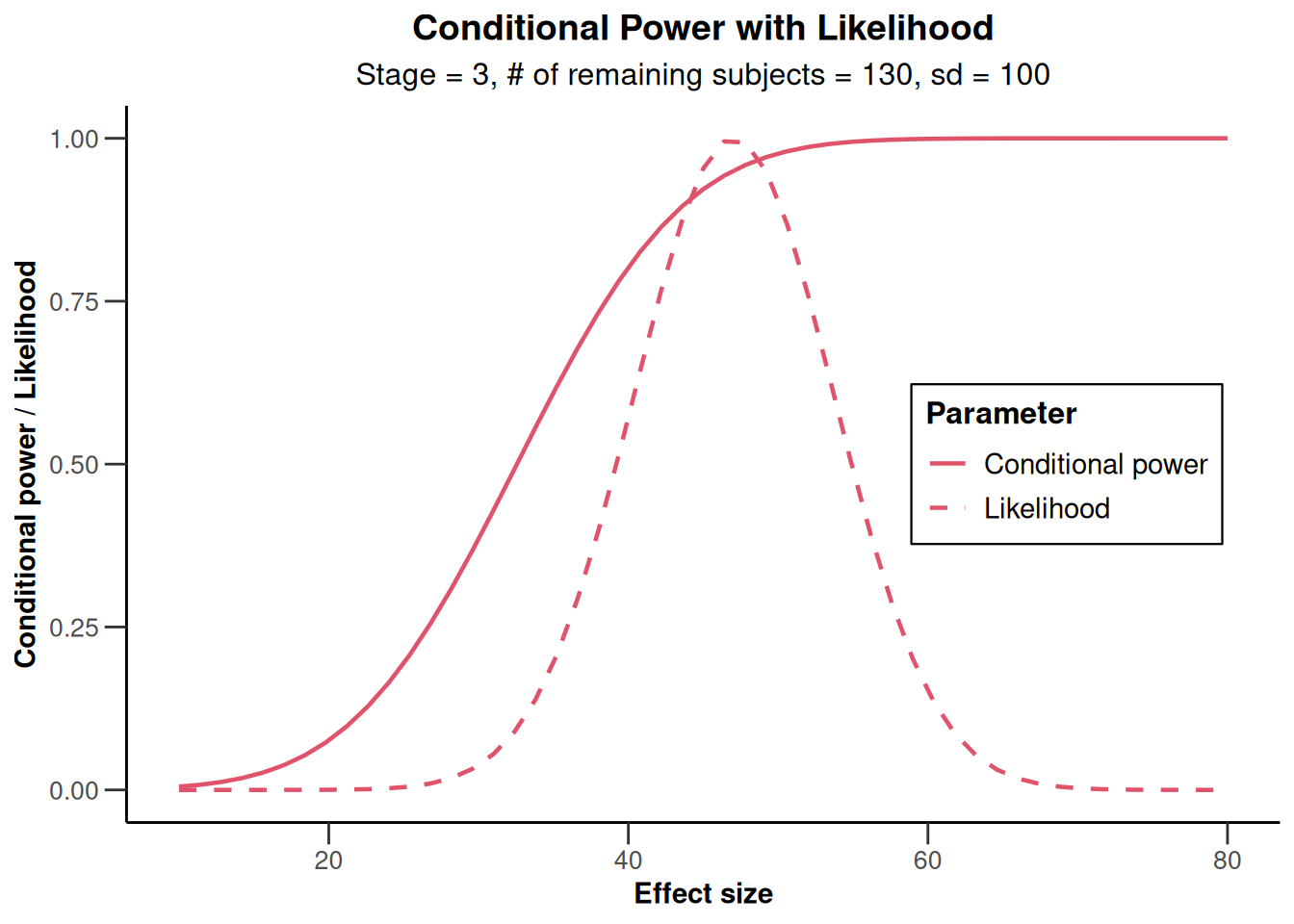
plot(x, type = 2)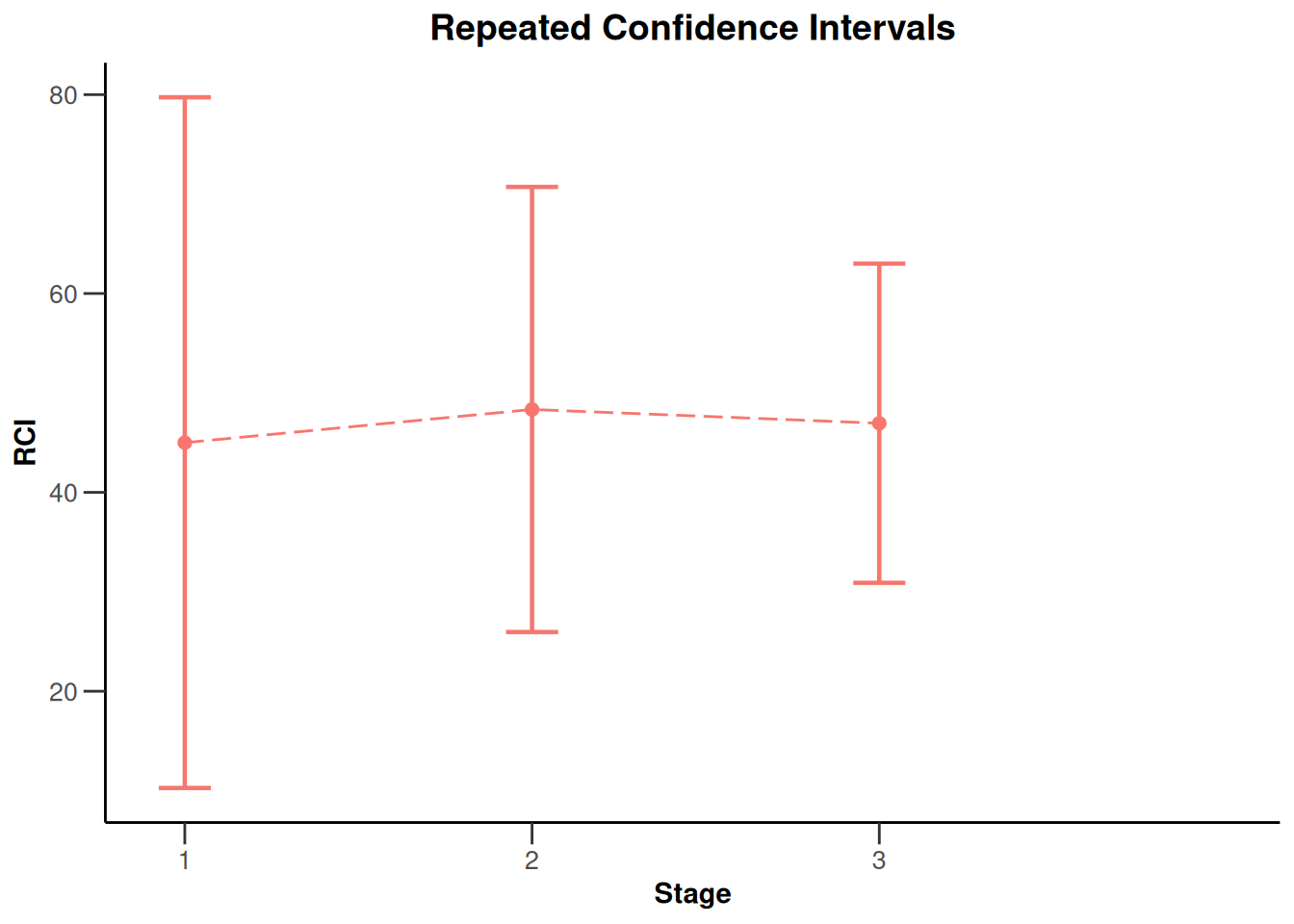
simpleDataExampleMeans2 <- getDataset(
n1 = c(23, 13, 22, 13),
n2 = c(22, 11, 22, 11),
means1 = c(2.7, 2.5, 4.5, 2.5) * 100,
means2 = c(1, 1.1, 1.3, 1) * 100,
stds1 = c(1.3, 2.4, 2.2, 1.3) * 100,
stds2 = c(1.2, 2.2, 2.1, 1.3) * 100
)
x <- getAnalysisResults(
design = designIN, dataInput = simpleDataExampleMeans2,
thetaH0 = 110, equalVariances = TRUE, directionUpper = TRUE, stage = 2
)
plot(x, nPlanned = c(20, 30))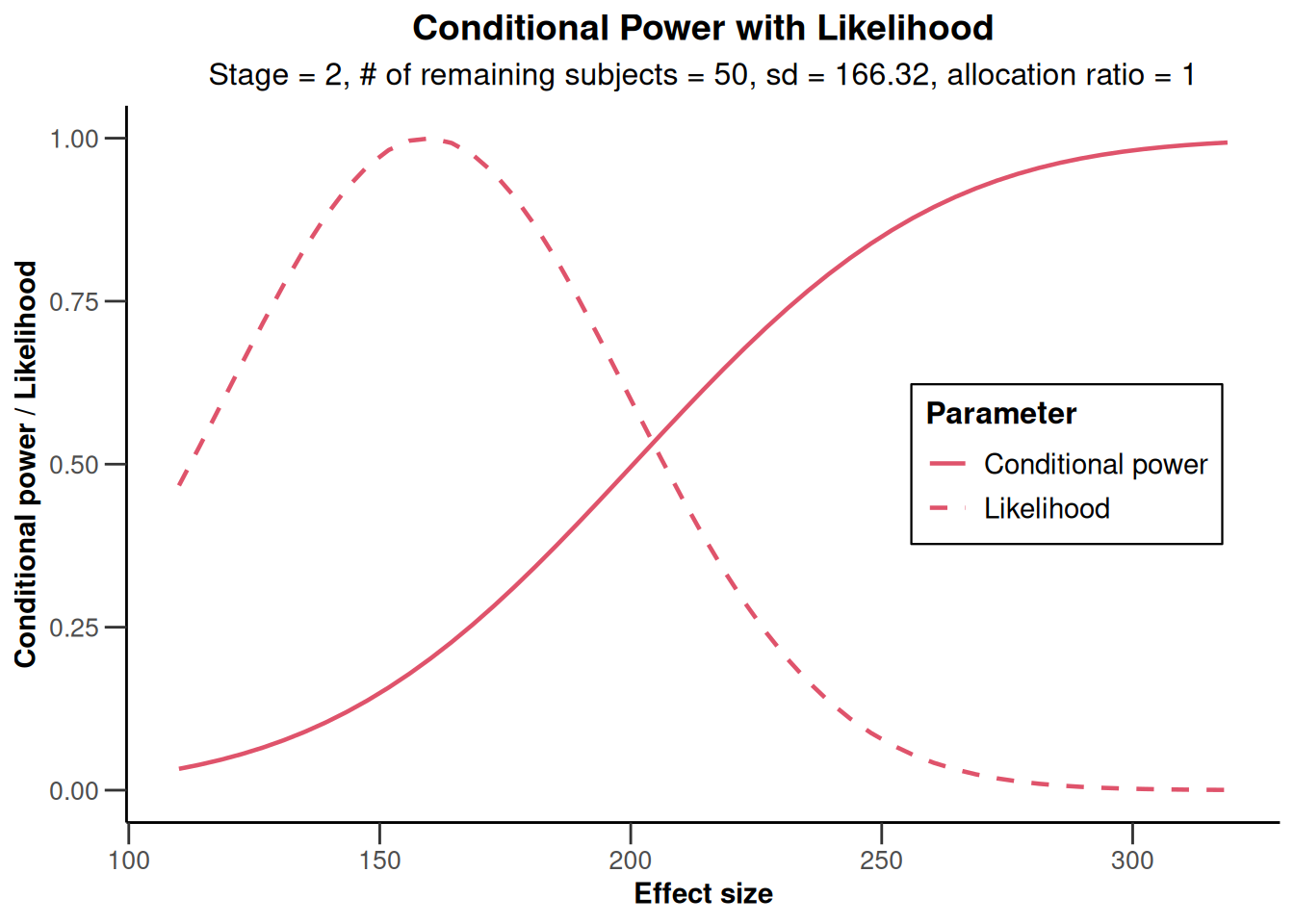
plot(x, type = 2)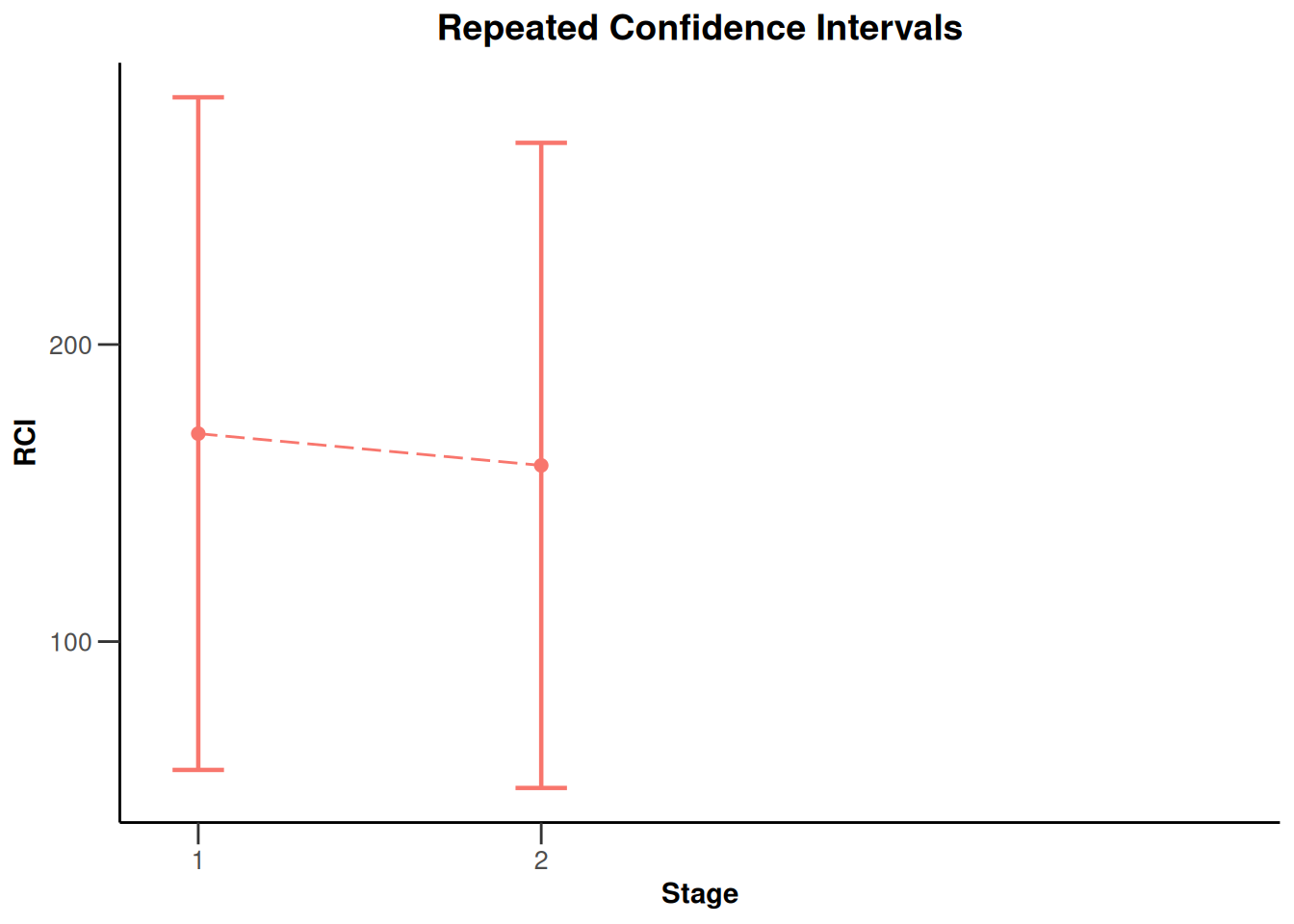
Analysis results base - rates
simpleDataExampleRates1 <- getDataset(
n = c(8, 10, 9, 11),
events = c(4, 5, 5, 6)
)
x <- getAnalysisResults(
design = designIN, dataInput = simpleDataExampleRates1,
stage = 3, thetaH0 = 0.75, normalApproximation = TRUE,
directionUpper = FALSE, nPlanned = 10
)Calculation of final confidence interval performed for kMax = 4 (for kMax > 2, it is theoretically shown that it is valid only if no sample size change was performed)plot(x)Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_line()`).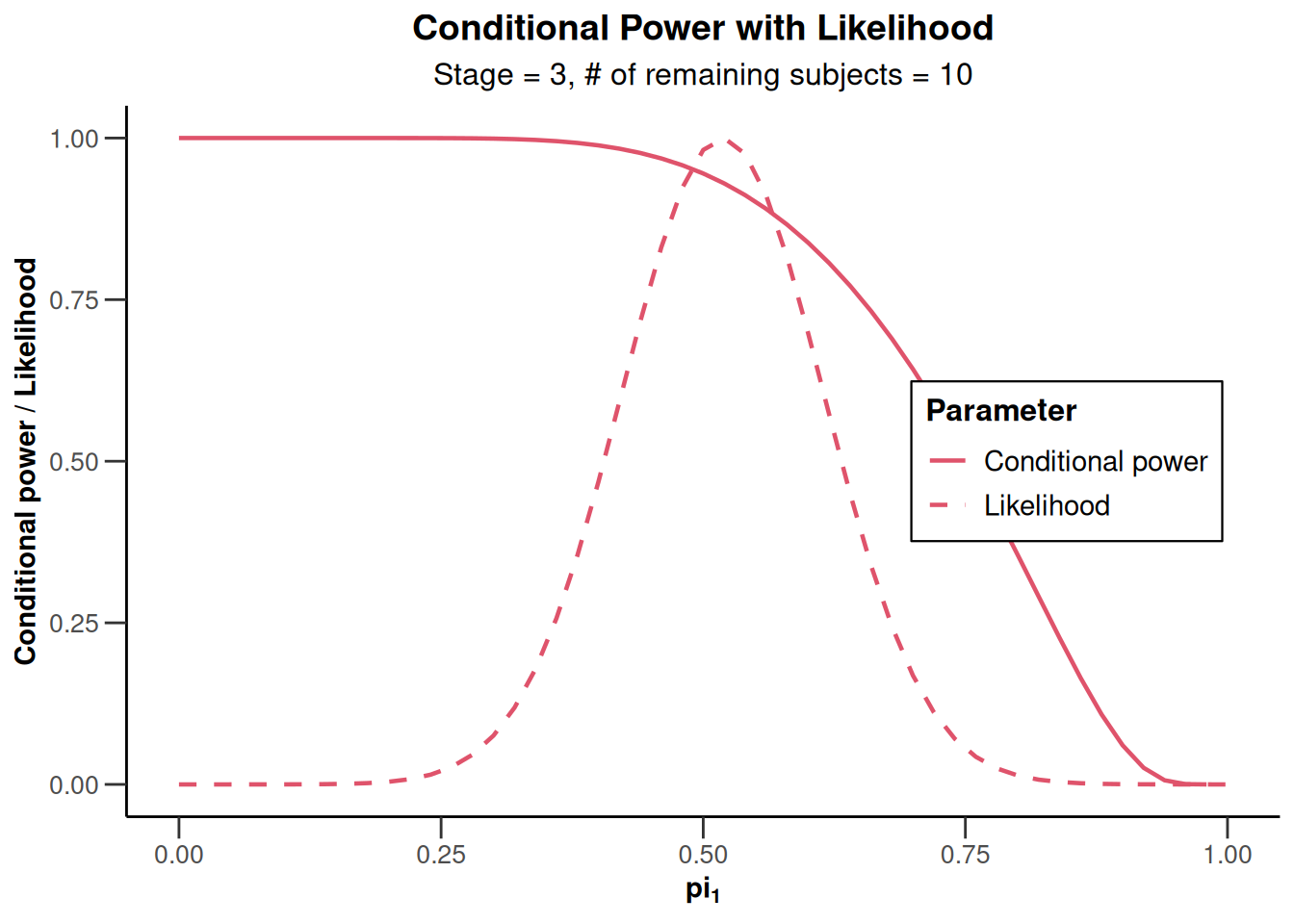
plot(x, type = 2)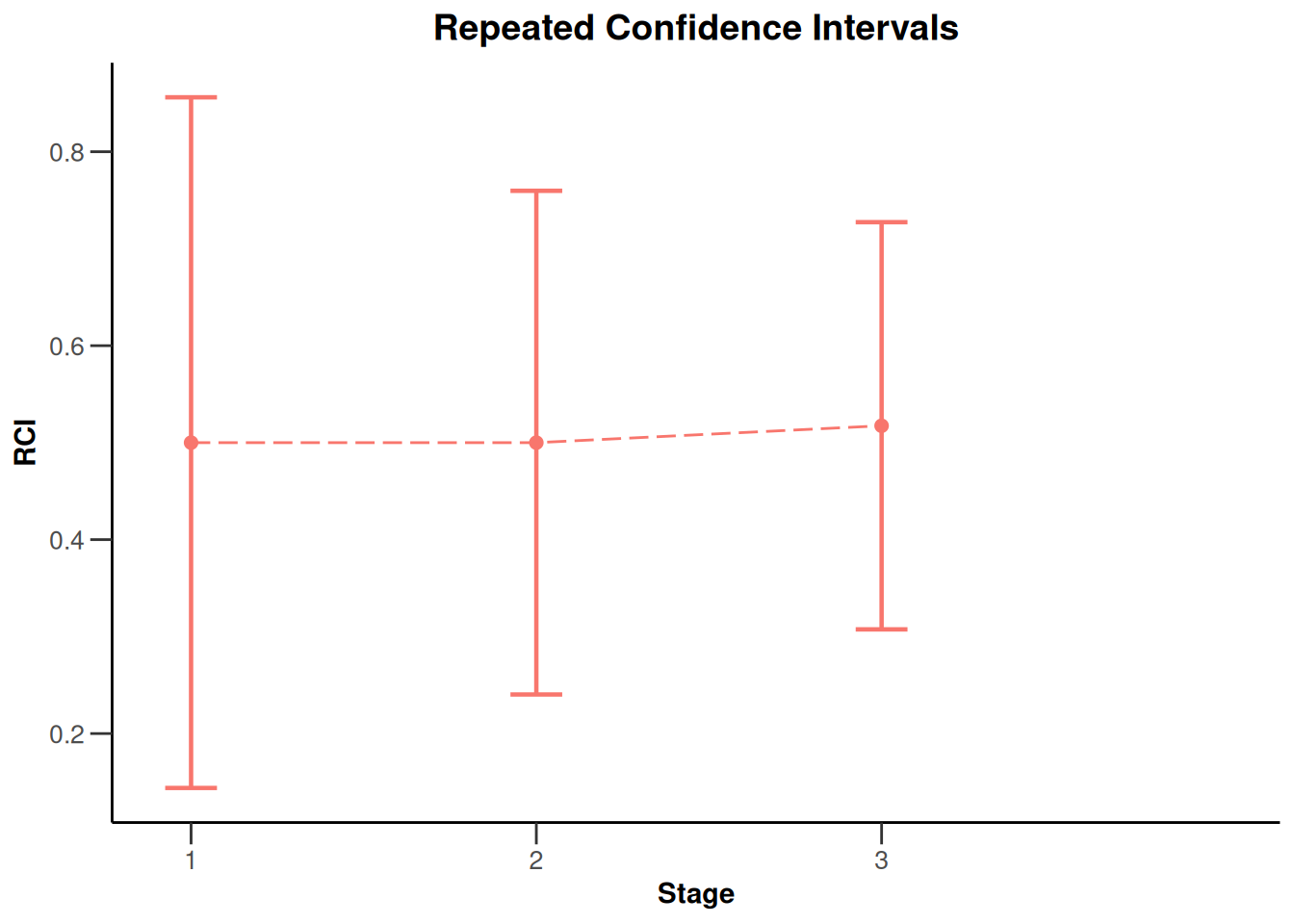
x <- getAnalysisResults(
design = designIN, dataInput = simpleDataExampleRates1,
stage = 3, thetaH0 = 0.75, normalApproximation = FALSE,
directionUpper = FALSE
)
plot(x, nPlanned = 20)Warning: Removed 1 row containing missing values or values outside the scale range
(`geom_line()`).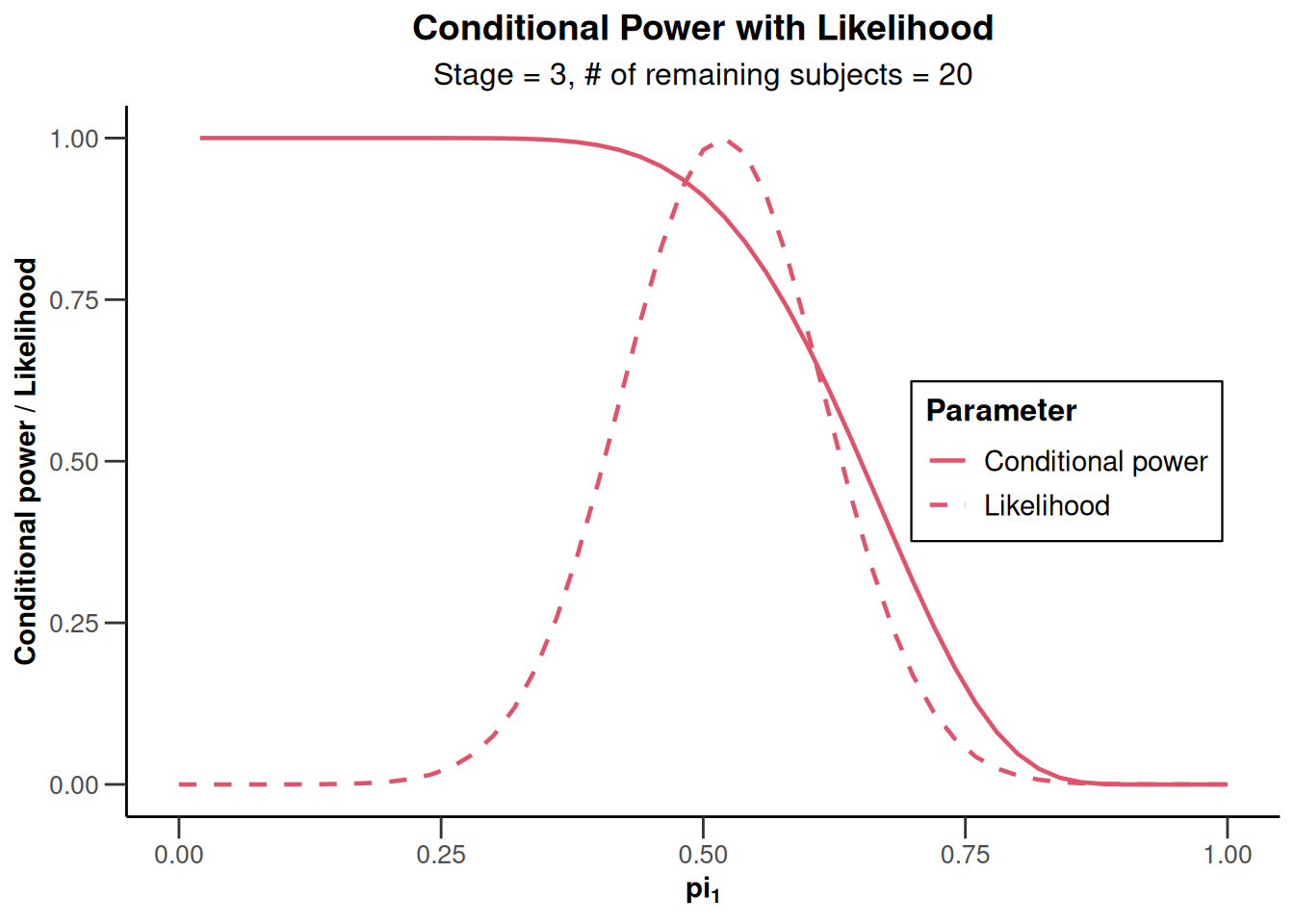
plot(x, type = 2)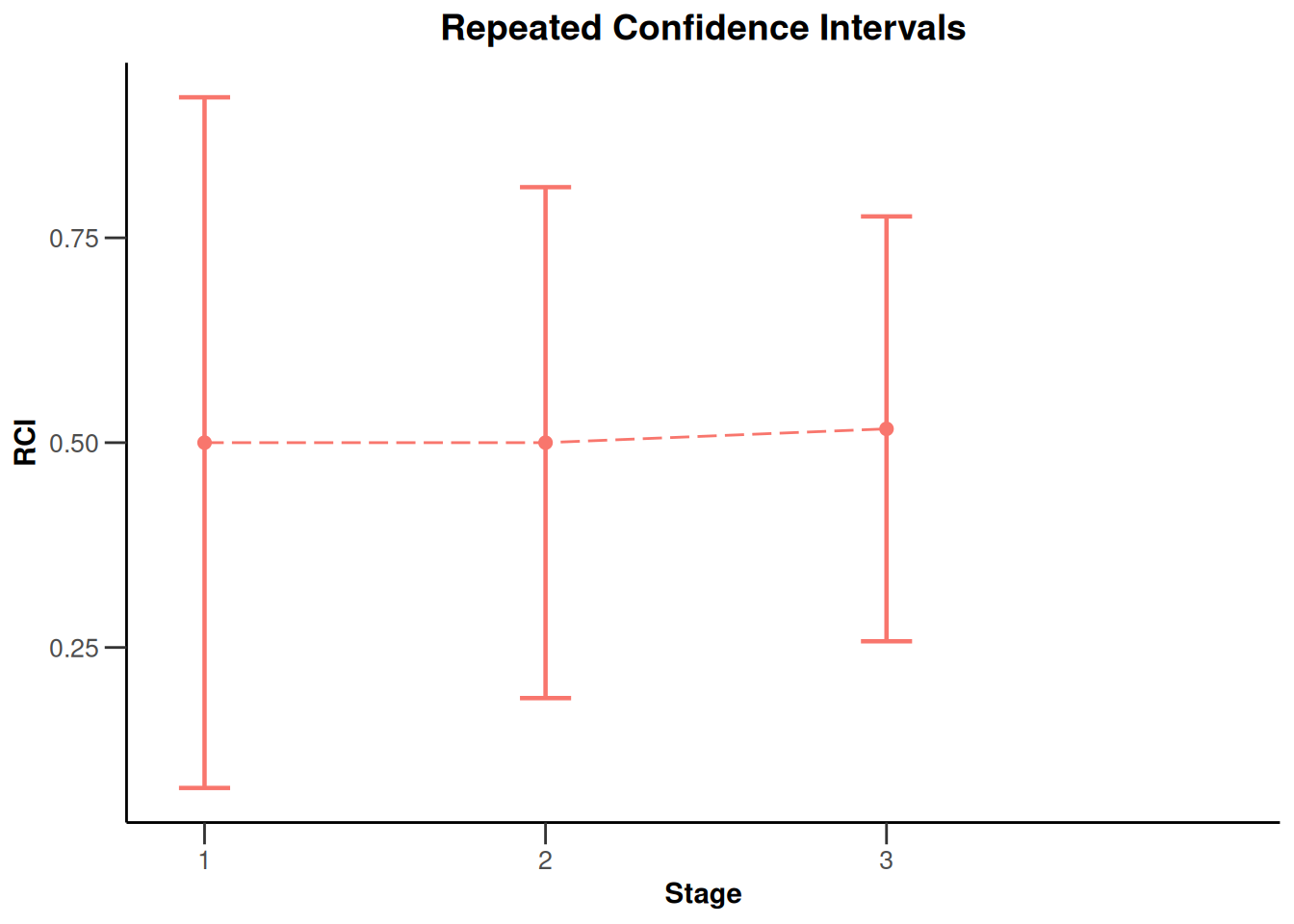
simpleDataExampleRates2 <- getDataset(
n1 = c(17, 23, 22),
n2 = c(18, 20, 19),
events1 = c(11, 12, 17),
events2 = c(5, 10, 7)
)
x <- getAnalysisResults(designIN, simpleDataExampleRates2,
thetaH0 = 0,
stage = 2, directionUpper = TRUE, normalApproximation = FALSE,
pi1 = 0.9, pi2 = 0.3, nPlanned = c(20, 20)
)Repeated confidence intervals will be calculated under the normal approximationplot(x, piTreatmentRange = c(0.2, 0.8))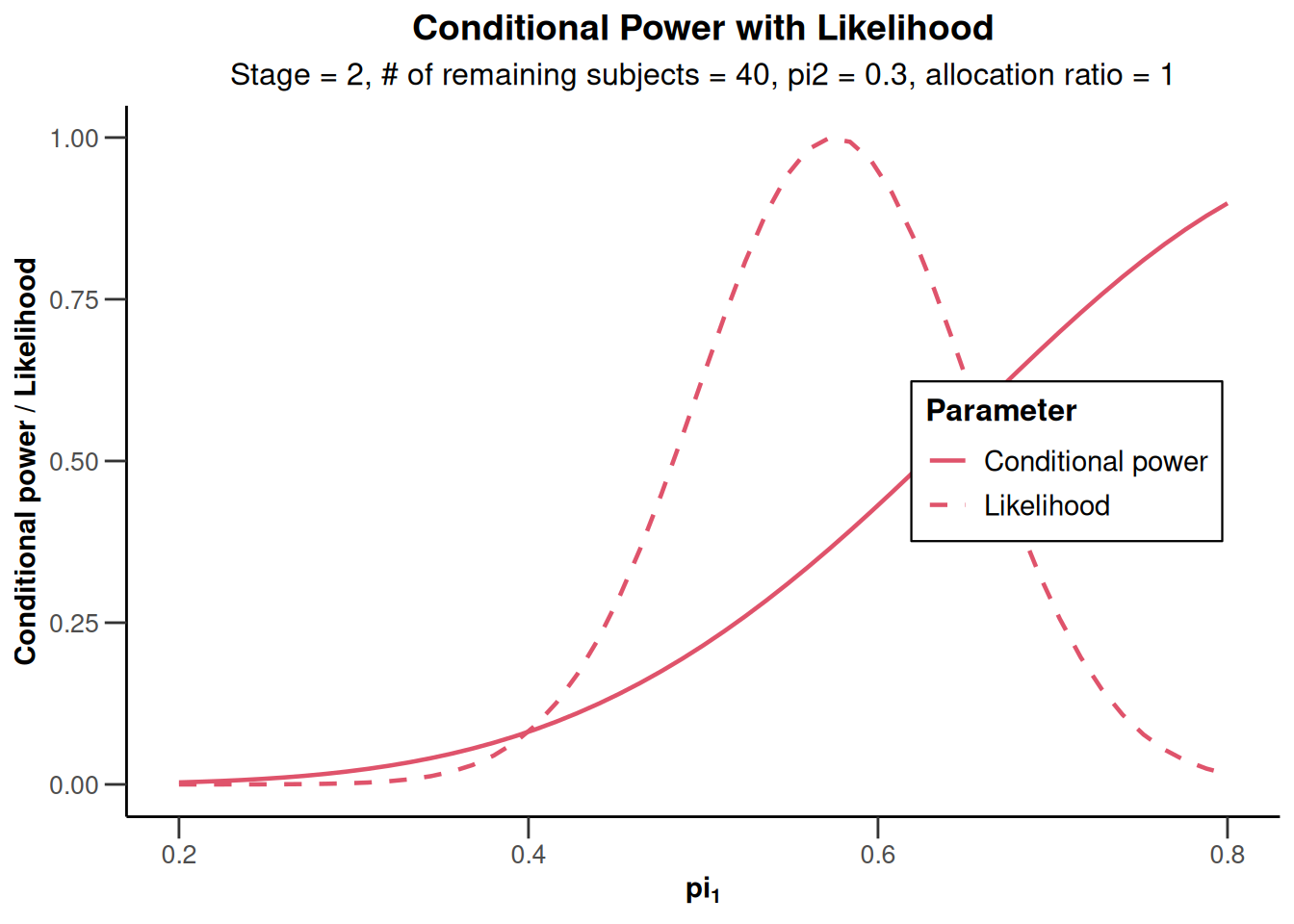
plot(x, type = 2)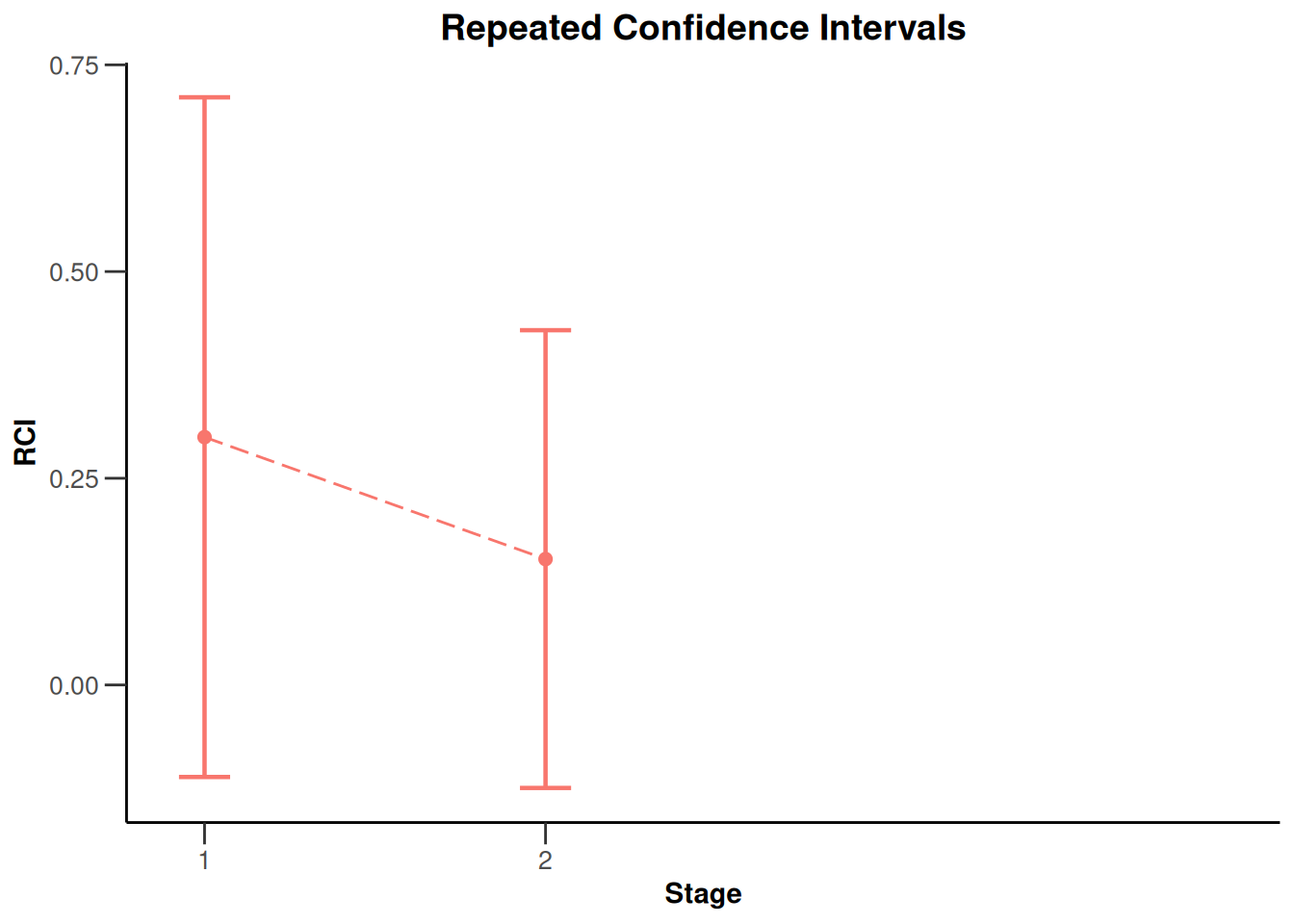
Analysis results base - survival
simpleDataExampleSurvival <- getDataset(
overallEvents = c(8, 15, 29),
overallAllocationRatios = c(1, 1, 1),
overallLogRanks = c(1.52, 1.38, 2.9)
)
x <- getAnalysisResults(designIN,
simpleDataExampleSurvival,
directionUpper = TRUE, nPlanned = 20
)Calculation of final confidence interval performed for kMax = 4 (for kMax > 2, it is theoretically shown that it is valid only if no sample size change was performed)plot(x, thetaRange = c(1, 3))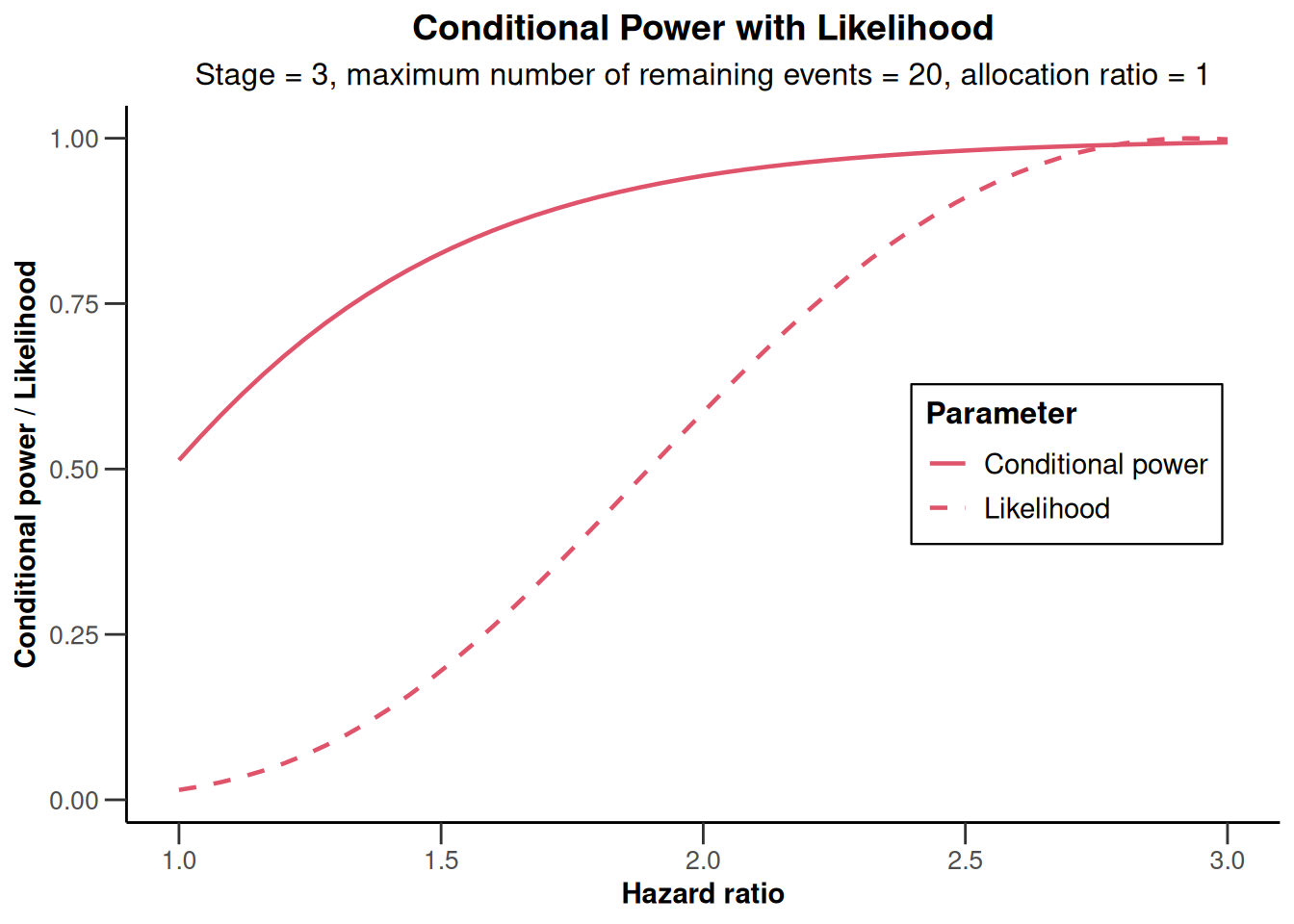
plot(x, type = 2)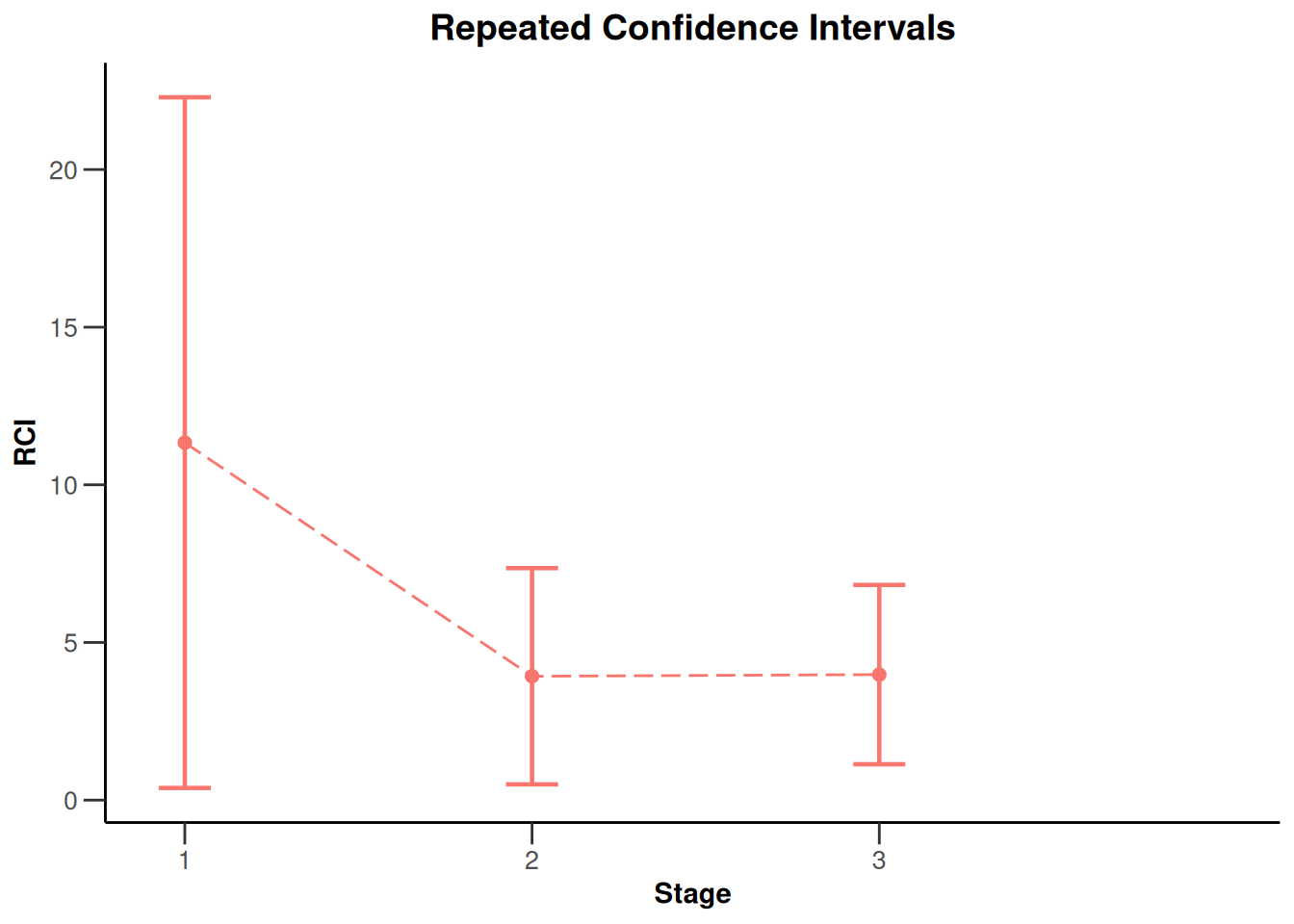
Analysis results multi-arm
Analysis results multi-arm - means
dataExampleMeans <- getDataset(
n1 = c(13, 25),
n2 = c(15, NA),
n3 = c(14, 27),
n4 = c(12, 29),
means1 = c(242, 222),
means2 = c(188, NA),
means3 = c(267, 277),
means4 = c(92, 122),
stDevs1 = c(244, 221),
stDevs2 = c(212, NA),
stDevs3 = c(256, 232),
stDevs4 = c(215, 227)
)
x <- getAnalysisResults(
design = designF, dataInput = dataExampleMeans,
intersectionTest = "Simes", directionUpper = TRUE,
varianceOption = "notPooled", nPlanned = c(32, 8),
assumedStDevs = c(200, NA, 240)
)
plot(x)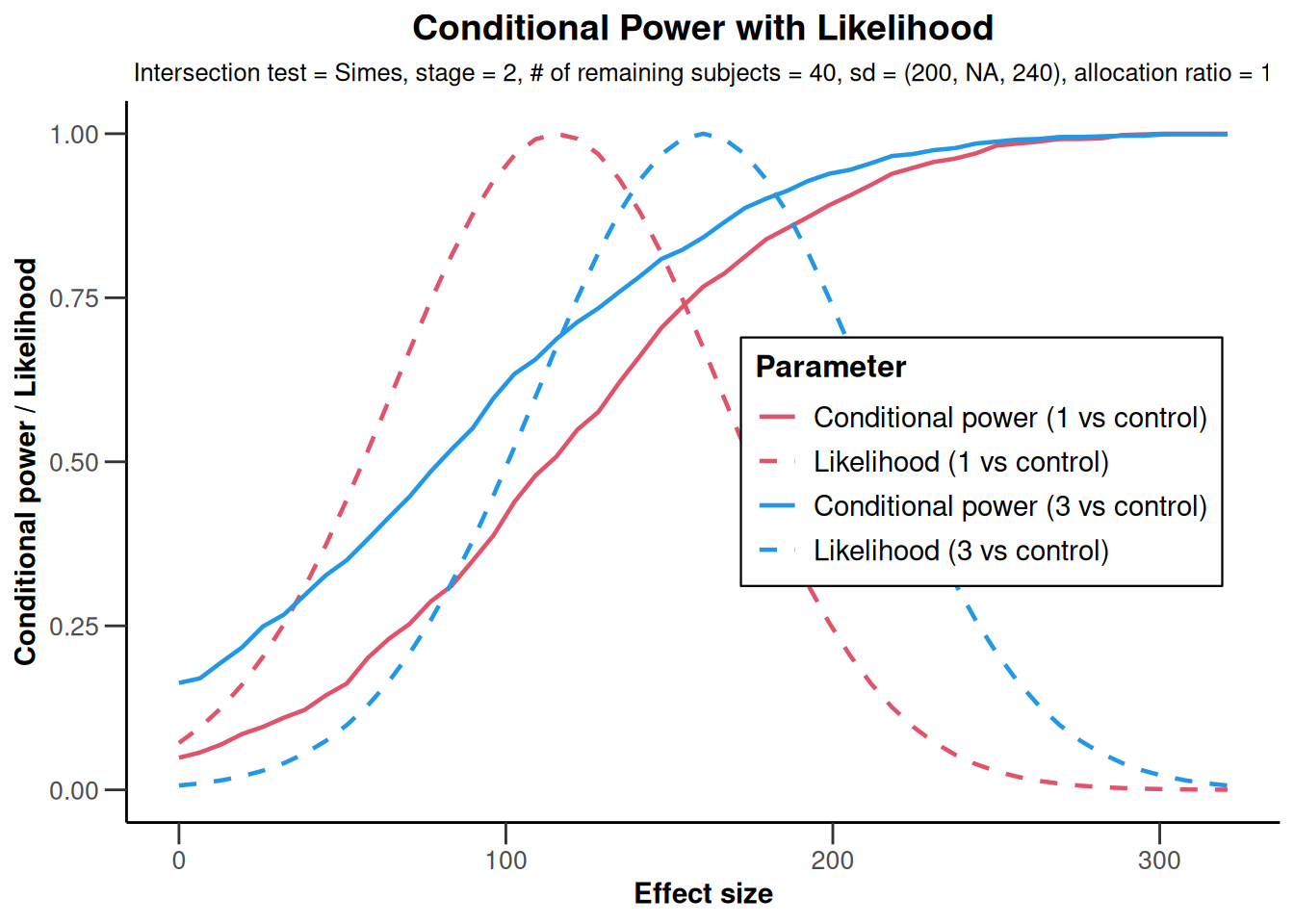
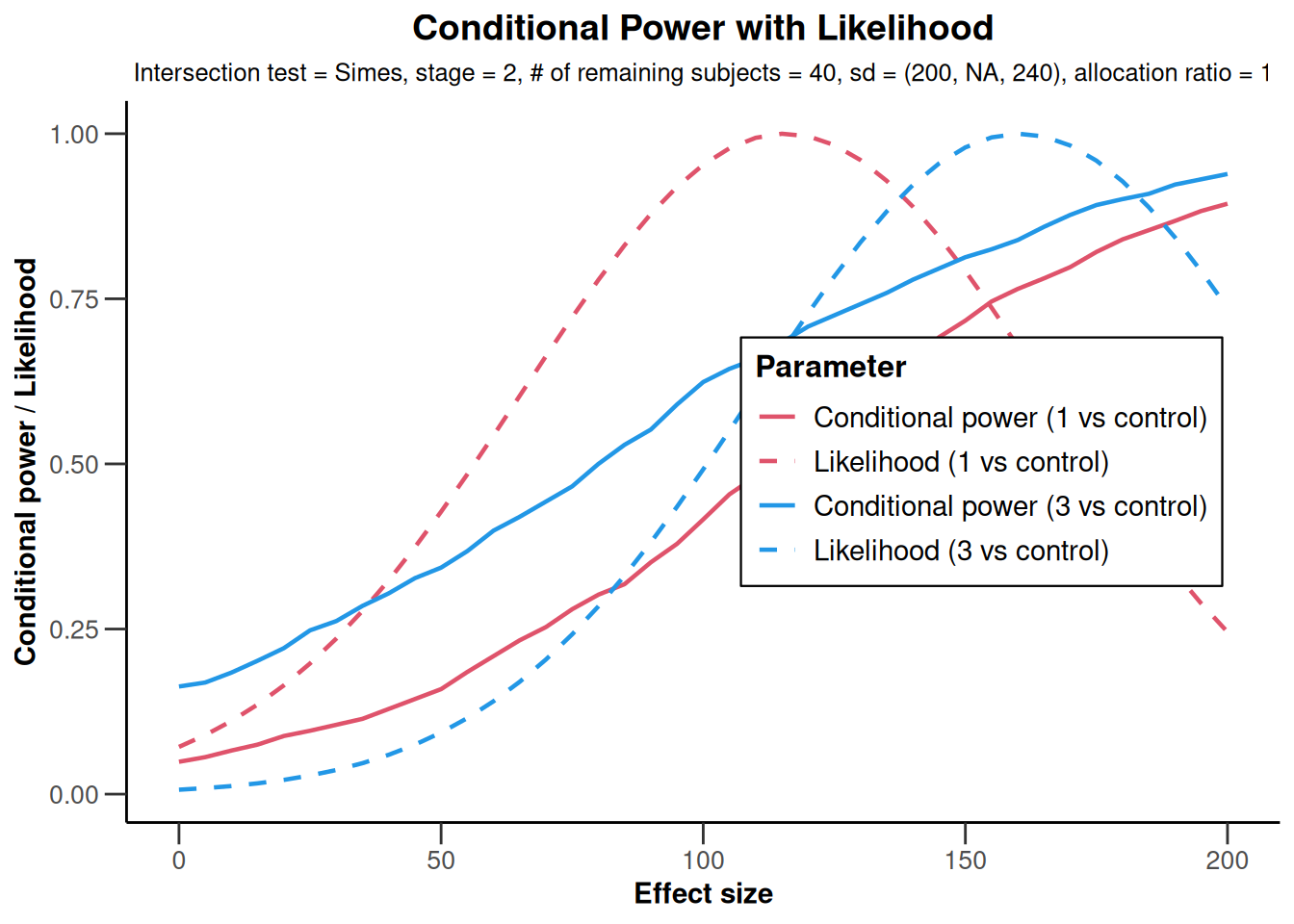
plot(x,
nPlanned = c(32, 8), thetaRange = seq(0, 200, 5),
assumedStDevs = c(200, NA, 240), treatmentArms = c(1, 3)
)
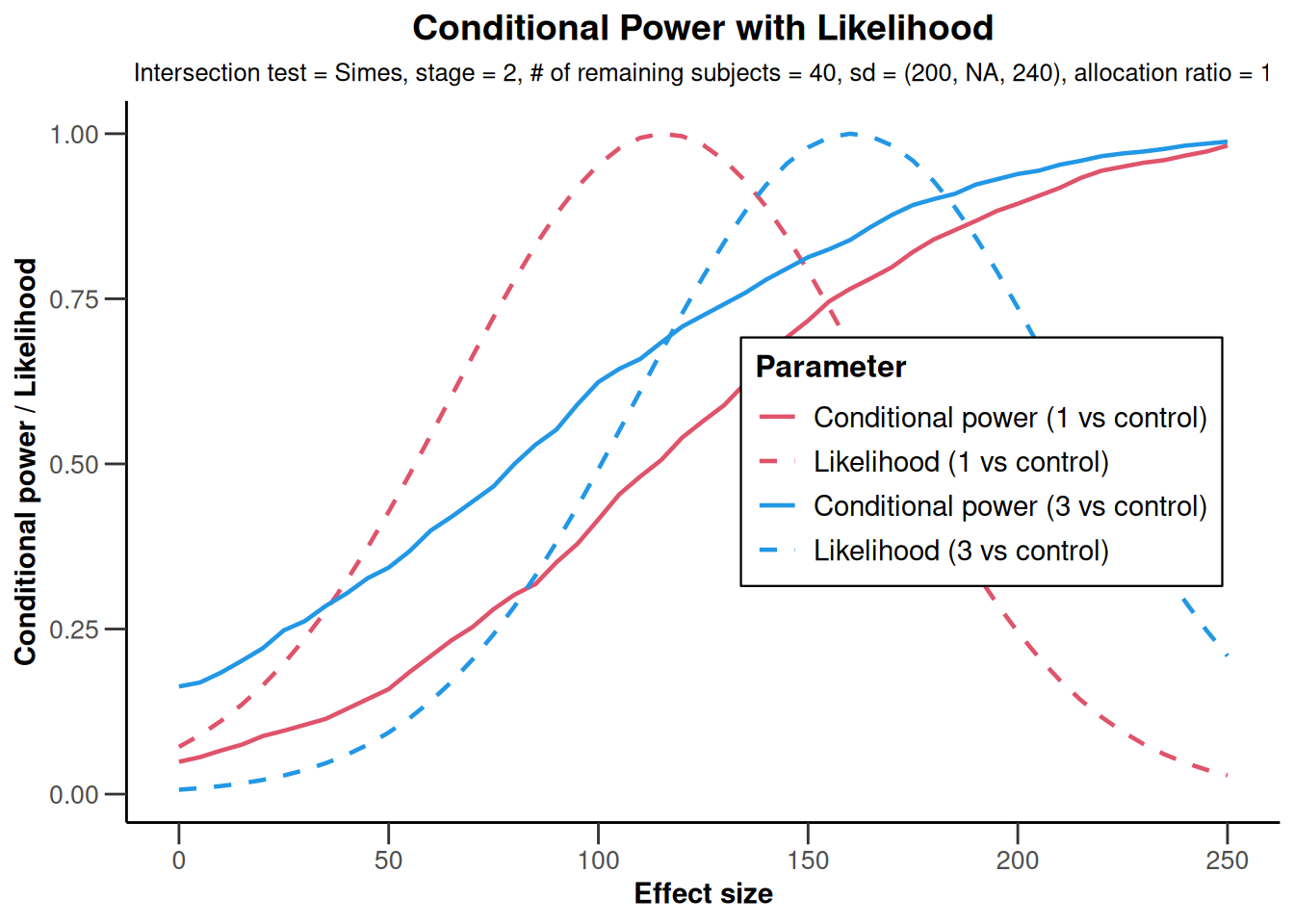
plot(x,
nPlanned = c(32, 8), thetaRange = c(0, 250),
assumedStDevs = c(200, NA, 240), treatmentArms = c(1, 3)
)
plot(x, type = 2)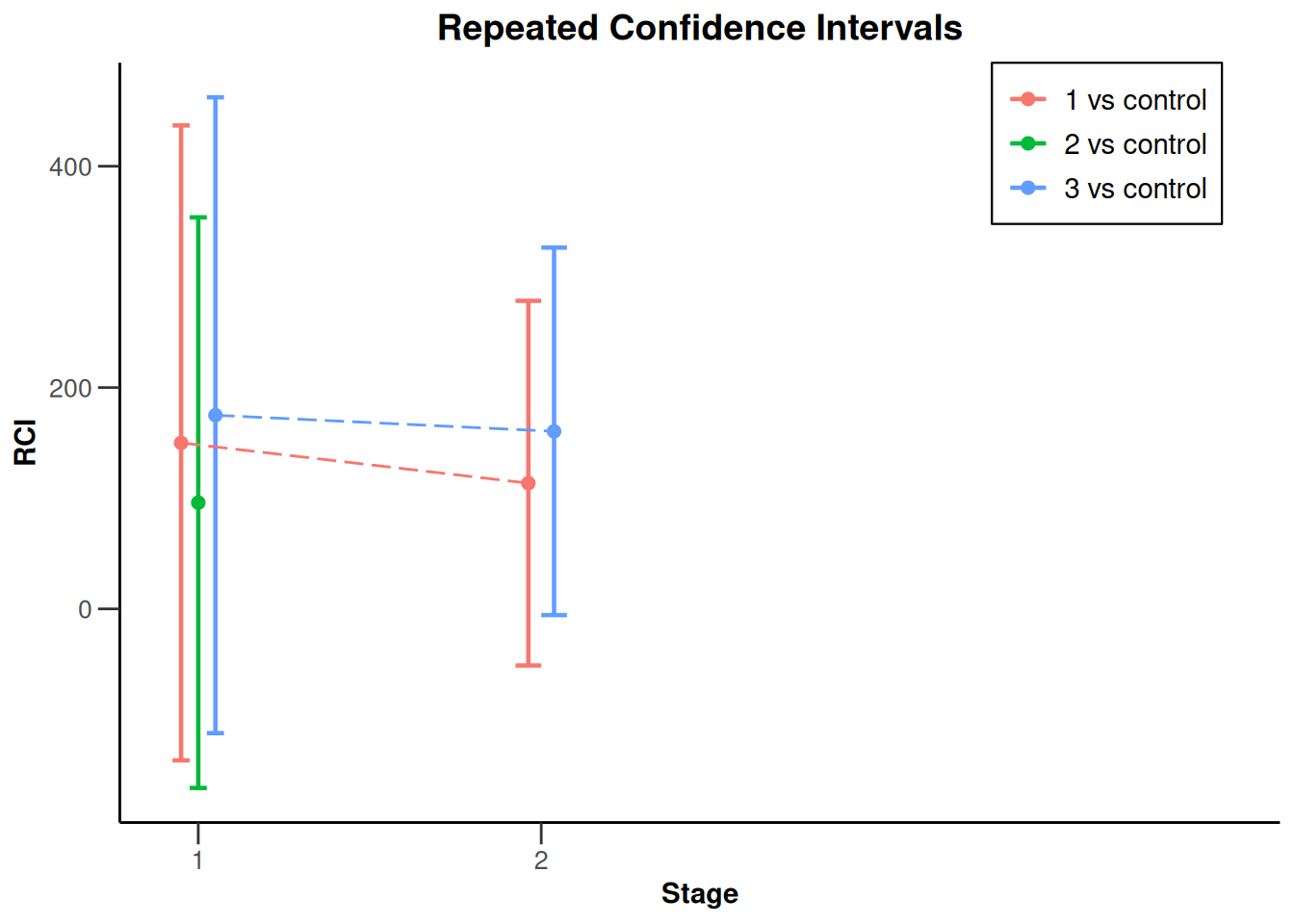
plot(x, type = 2, treatmentArms = c(1, 3))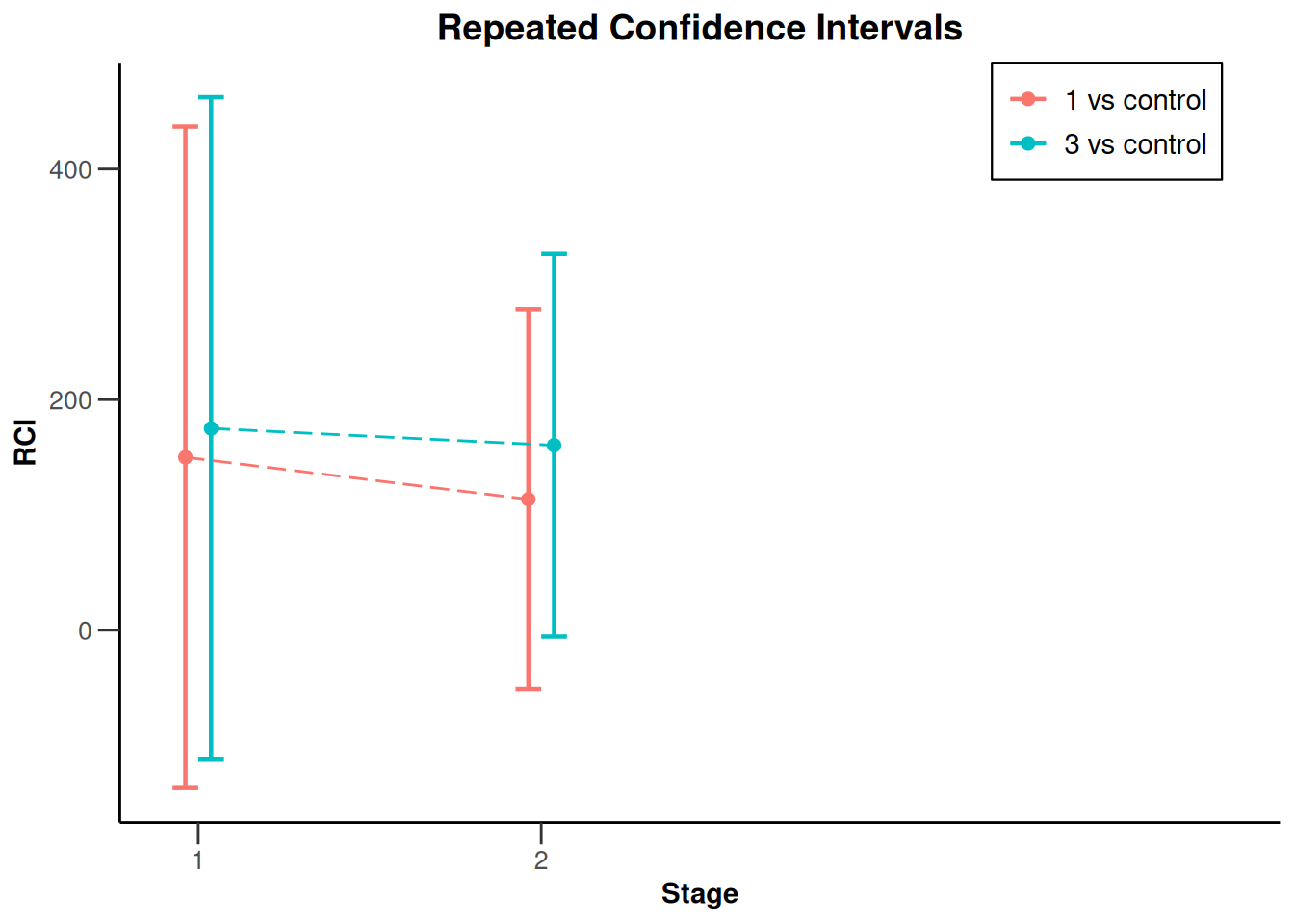
plot(x, type = 2, treatmentArms = c(1))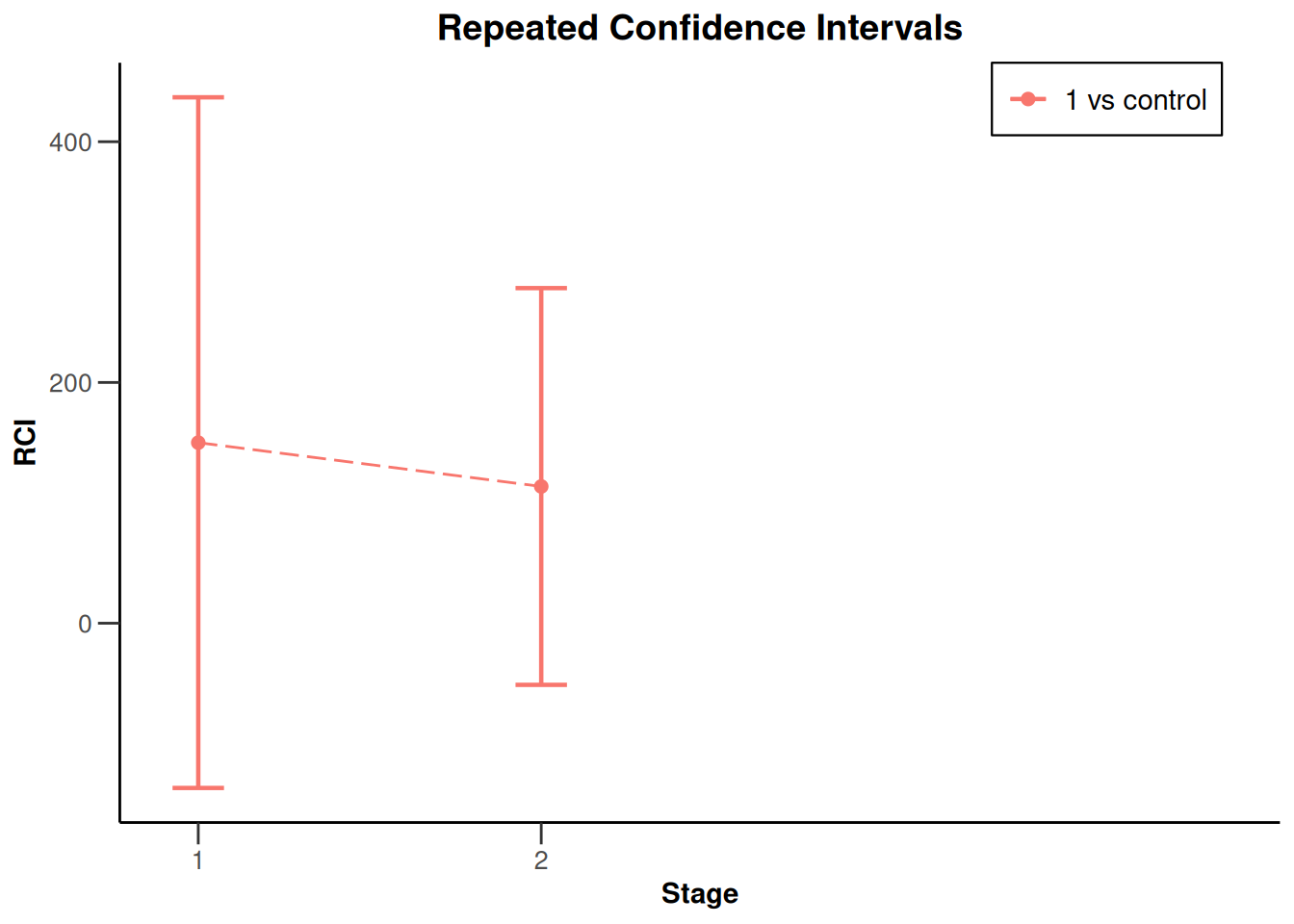
plot(x, type = 2, treatmentArms = c(2))`geom_line()`: Each group consists of only one observation.
ℹ Do you need to adjust the group aesthetic?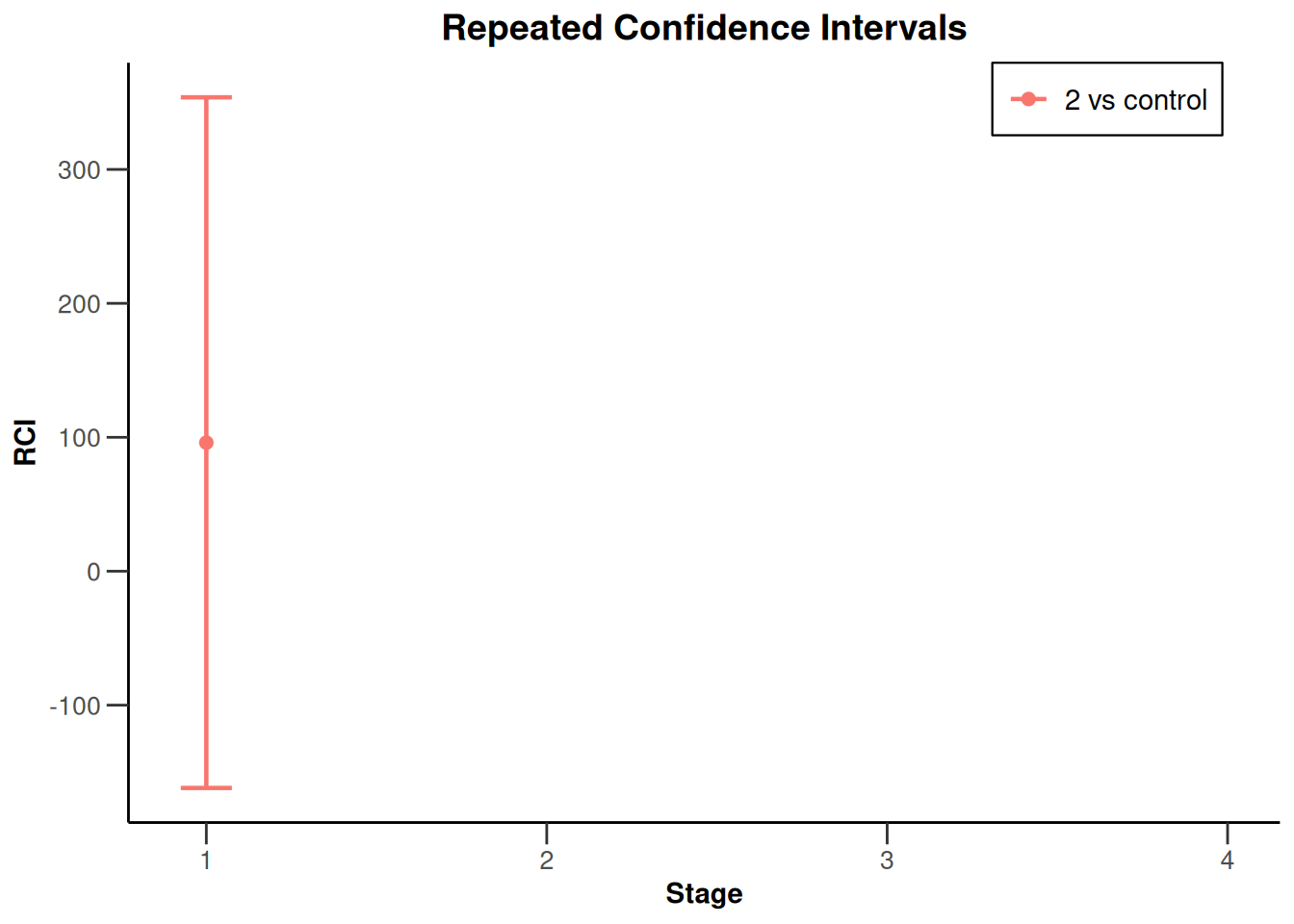
plot(x, type = 2, treatmentArms = c(3))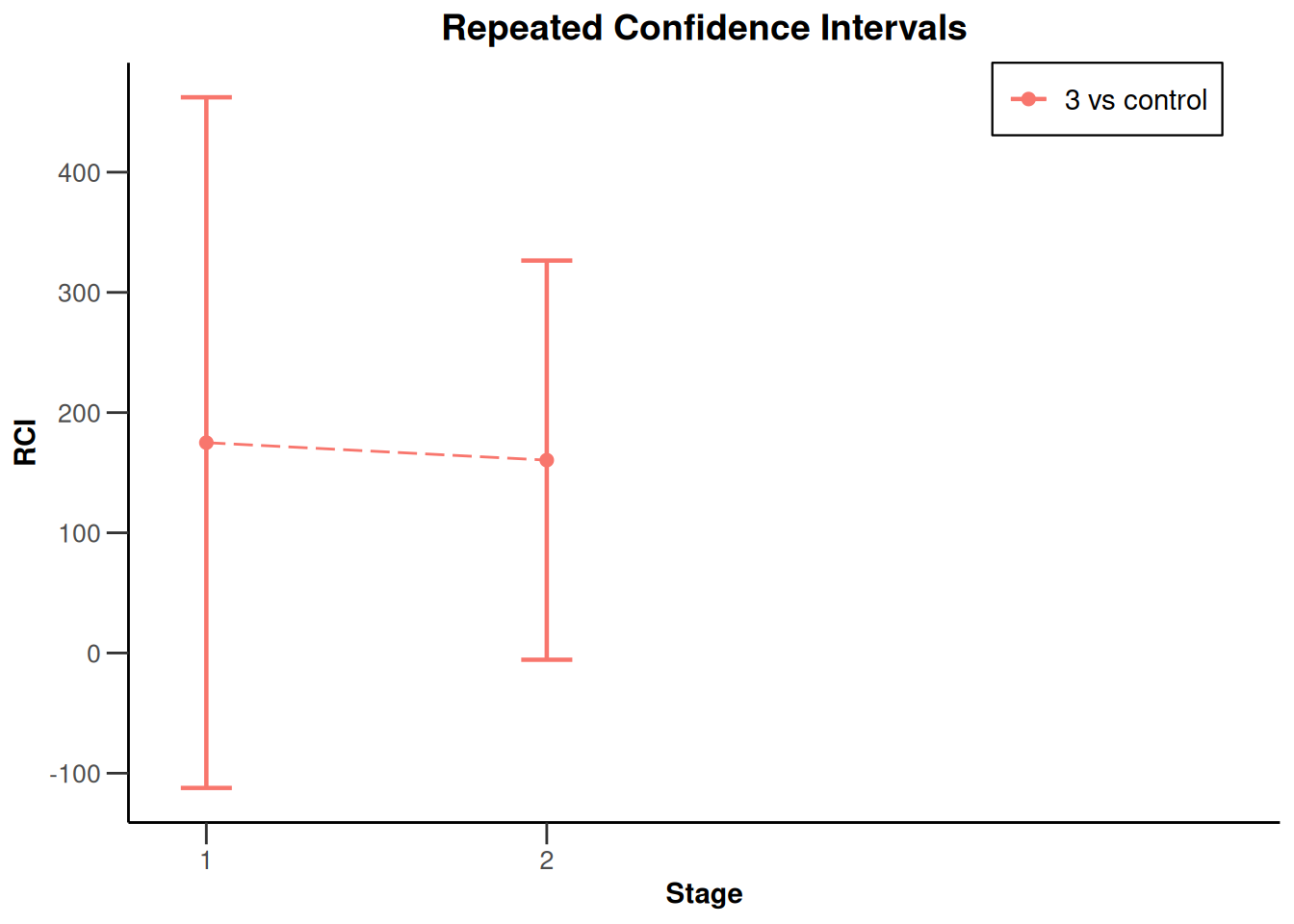
x2 <- getAnalysisResults(
design = designIN, dataInput = dataExampleMeans,
intersectionTest = "Simes", directionUpper = TRUE,
varianceOption = "notPooled", nPlanned = c(32, 8)
)
# Observed standard deviations will be used
plot(x2)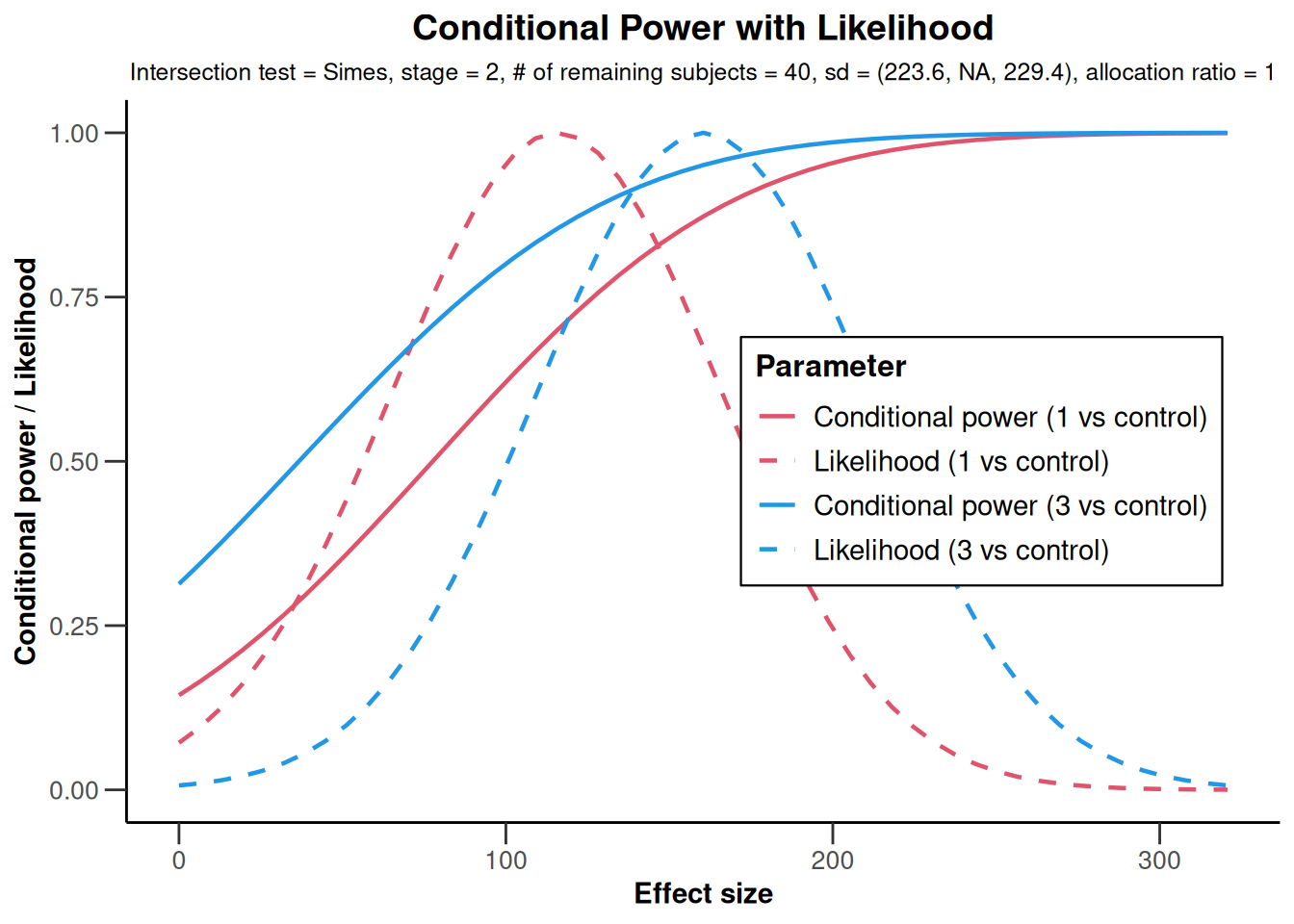
Analysis results multi-arm - rates
dataExampleRates <- getDataset(
n1 = c(23, 25),
n2 = c(25, NA),
n3 = c(24, 27),
n4 = c(22, 29),
events1 = c(15, 12),
events2 = c(19, NA),
events3 = c(18, 22),
events4 = c(12, 13)
)
analysisResultsRates <- getAnalysisResults(
design = designIN,
dataInput = dataExampleRates, intersectionTest = "Simes",
nPlanned = c(20, 20), directionUpper = TRUE, piControl = 0.2
)
plot(analysisResultsRates)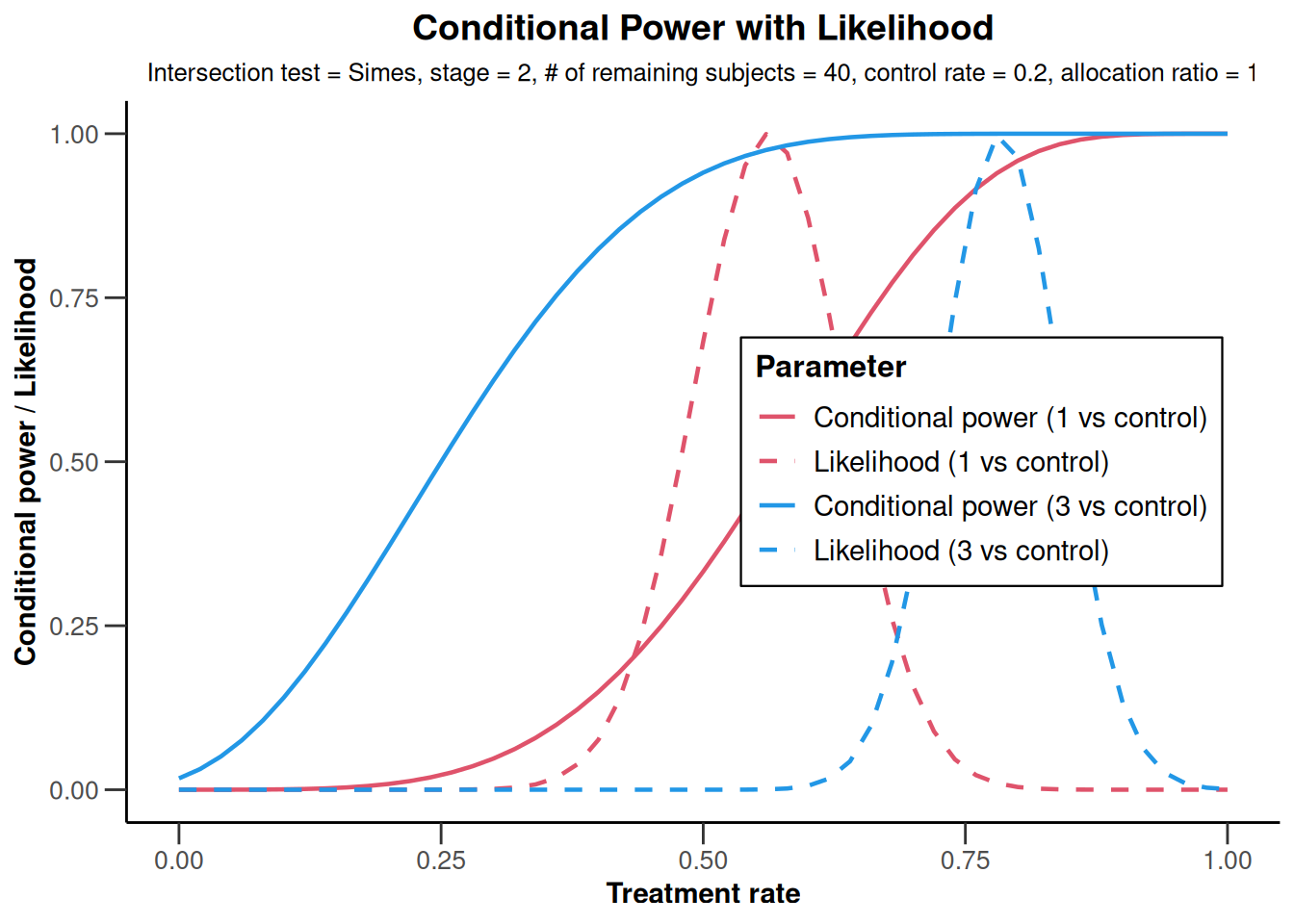
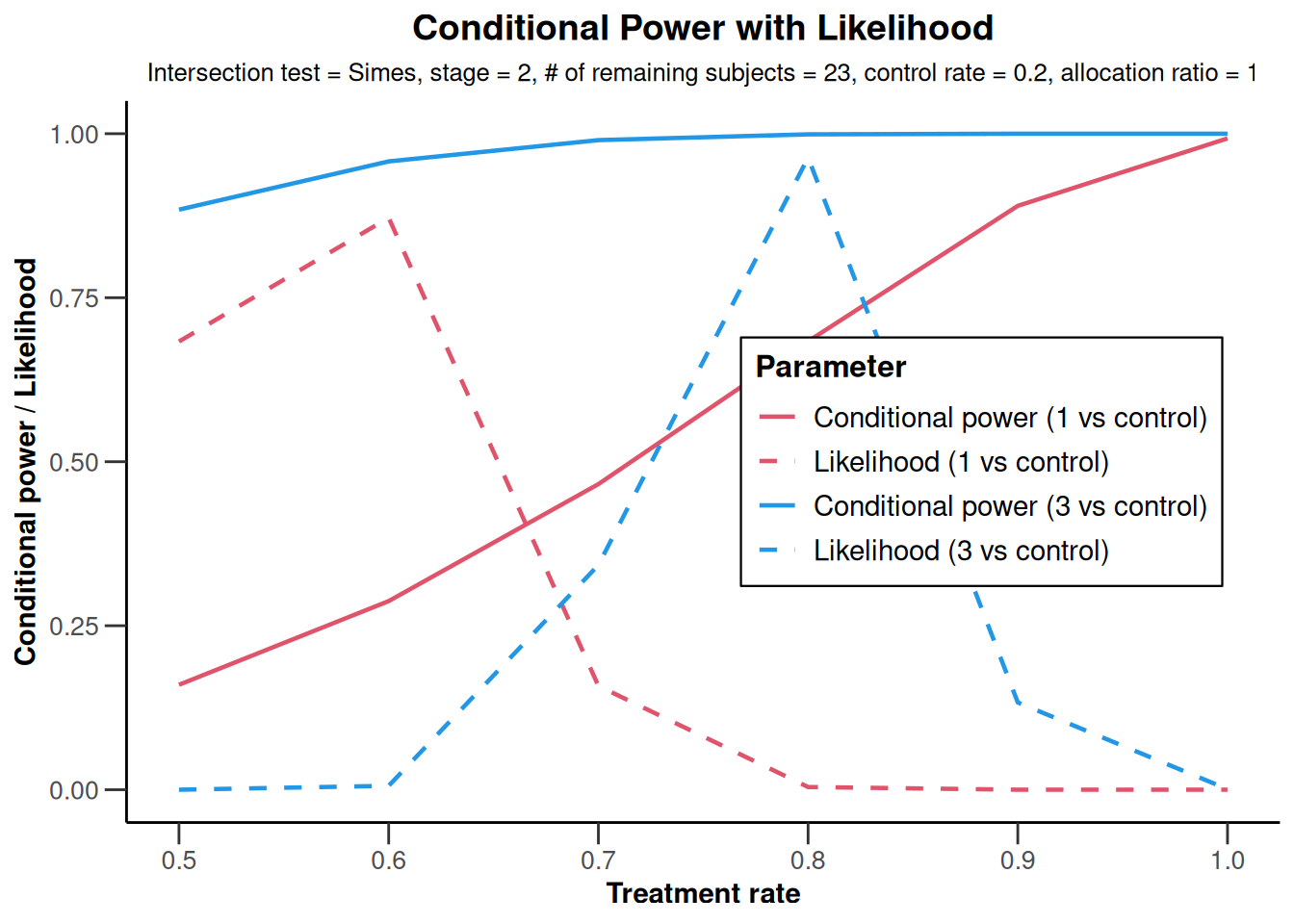
plot(analysisResultsRates,
nPlanned = c(20, 3),
piTreatmentRange = seq(0.5, 1, 0.1)
)
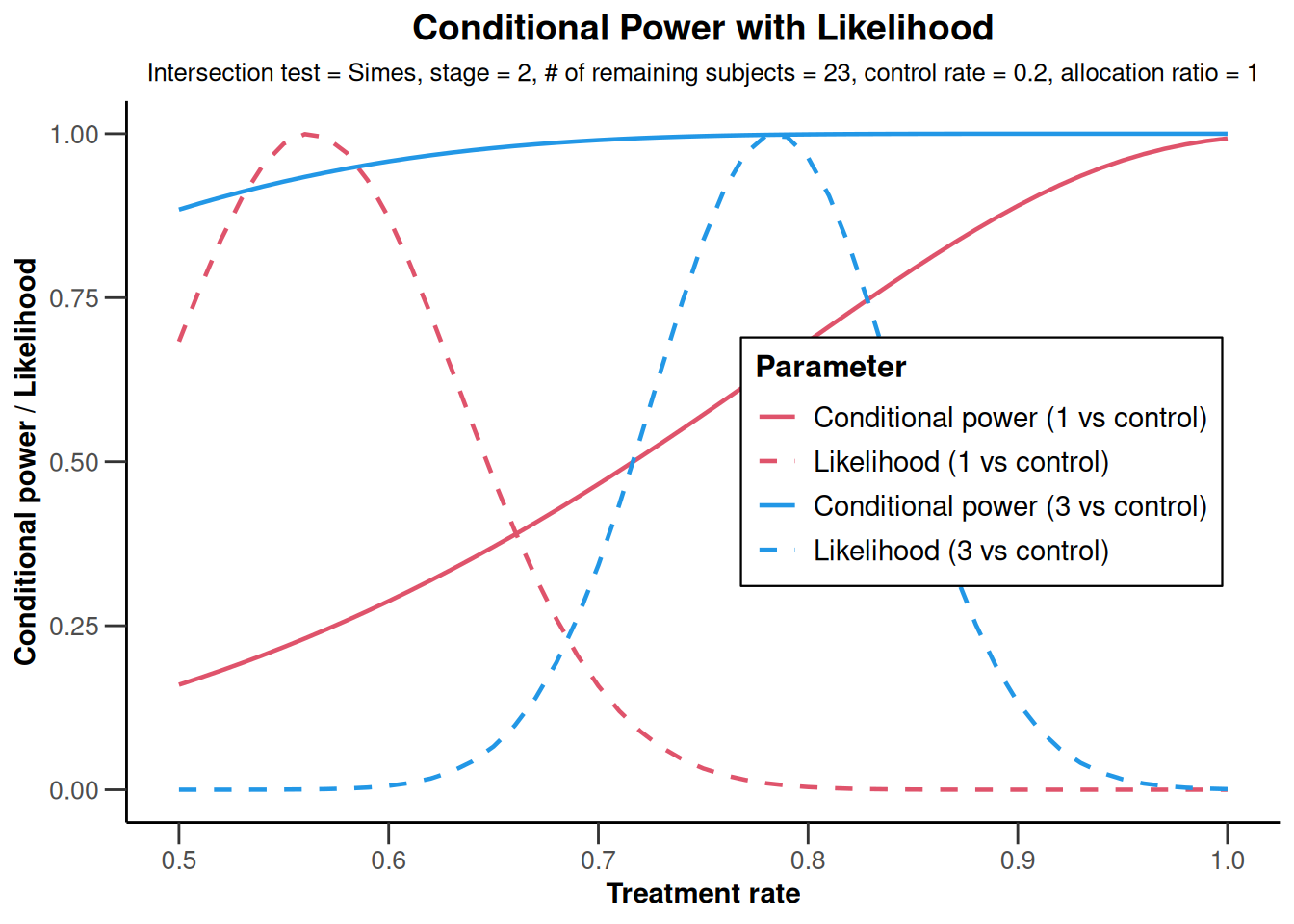
plot(analysisResultsRates,
nPlanned = c(20, 3),
piTreatmentRange = c(0.5, 1)
)
plot(analysisResultsRates, nPlanned = c(20, 3))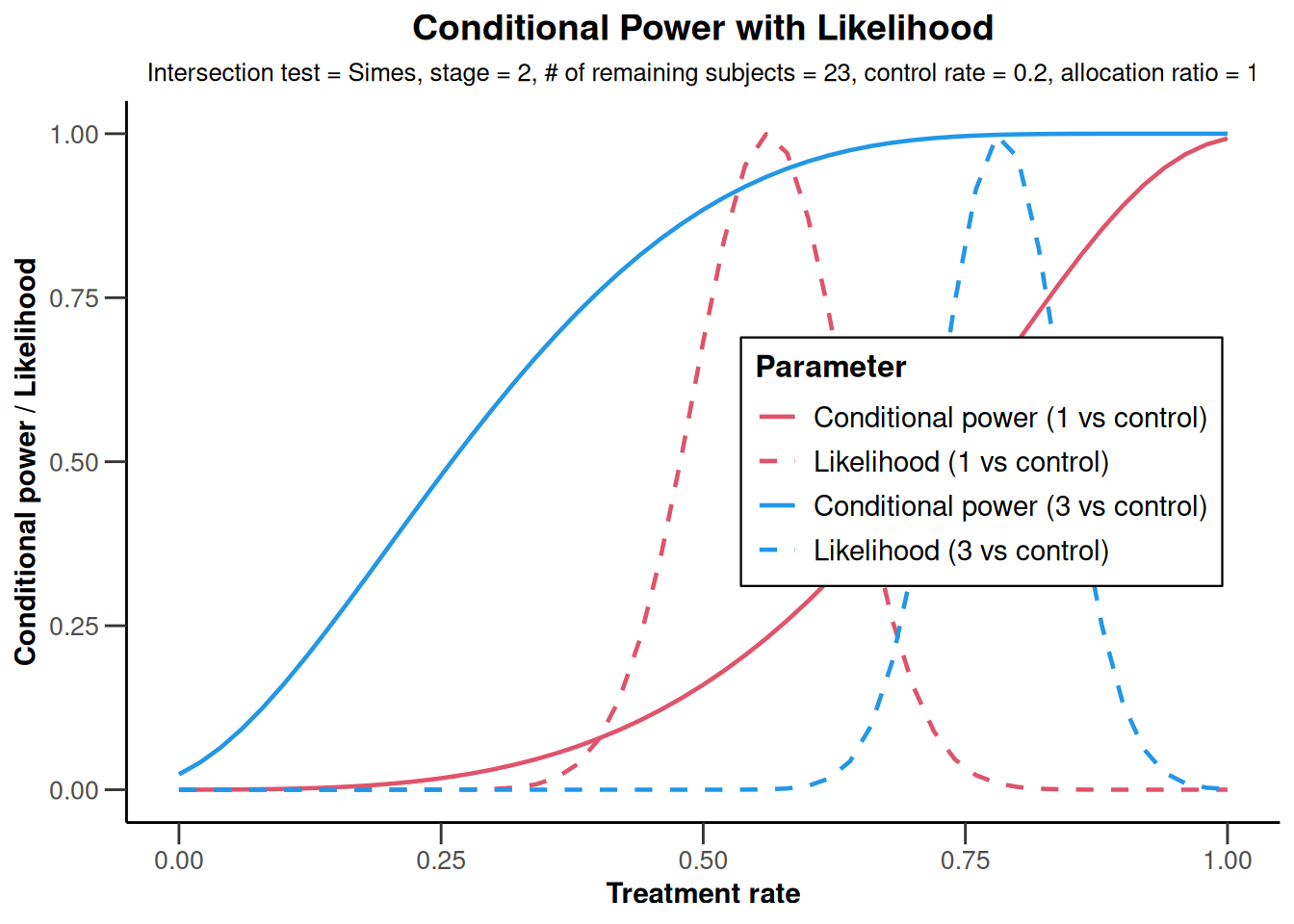
plot(analysisResultsRates, type = 2)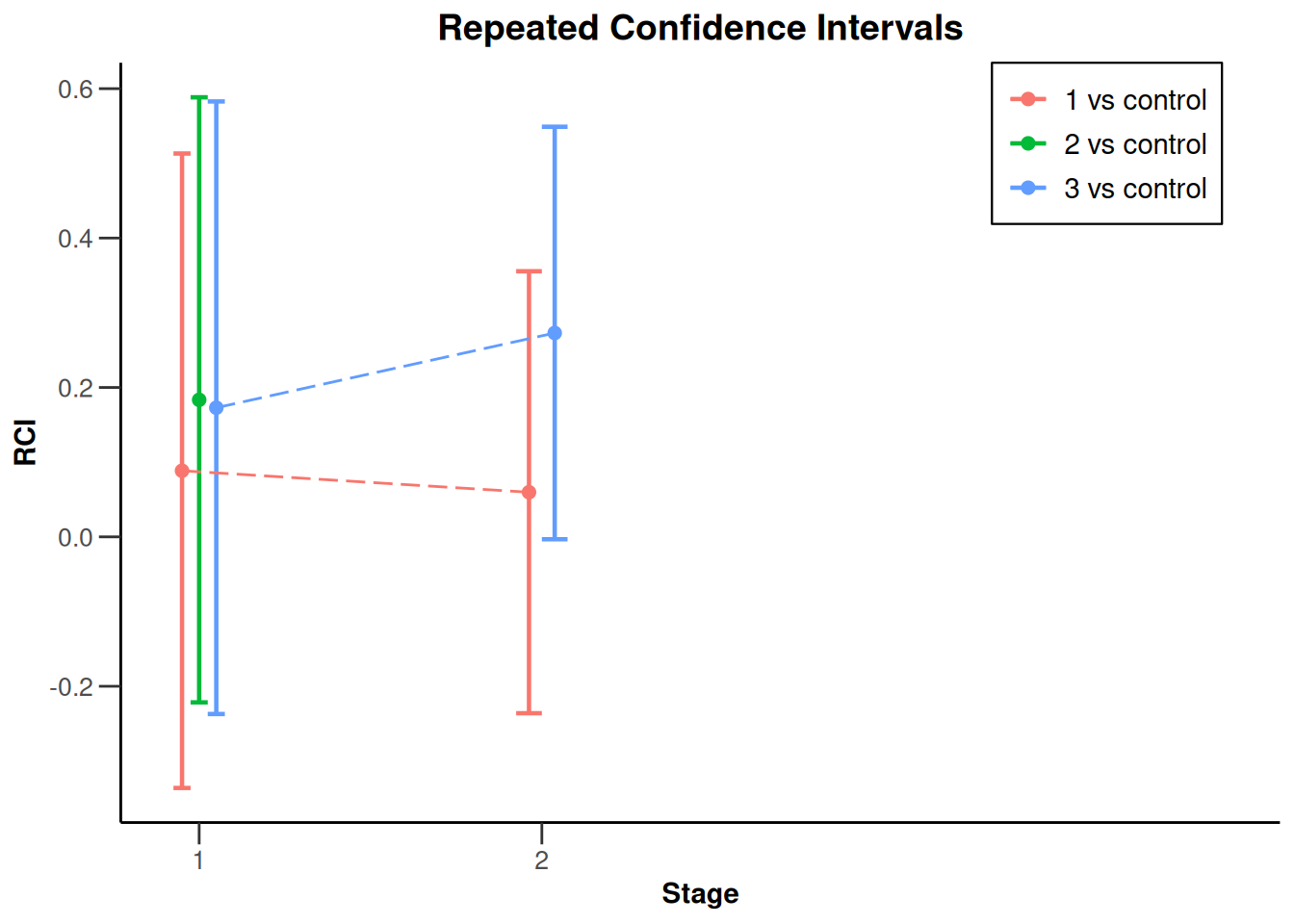
Analysis results multi-arm - survival
dataExampleSurvival <- getDataset(
events1 = c(25, 32),
events2 = c(18, NA),
events3 = c(22, 36),
logRanks1 = c(1.9, 1.8),
logRanks2 = c(1.99, NA),
logRanks3 = c(2.52, 2.11)
)
analysisResultsSurvival <- getAnalysisResults(
design = getDesignInverseNormal(),
dataInput = dataExampleSurvival, intersectionTest = "Simes",
nPlanned = 20, thetaH0 = 1.2, directionUpper = TRUE
)
plot(analysisResultsSurvival)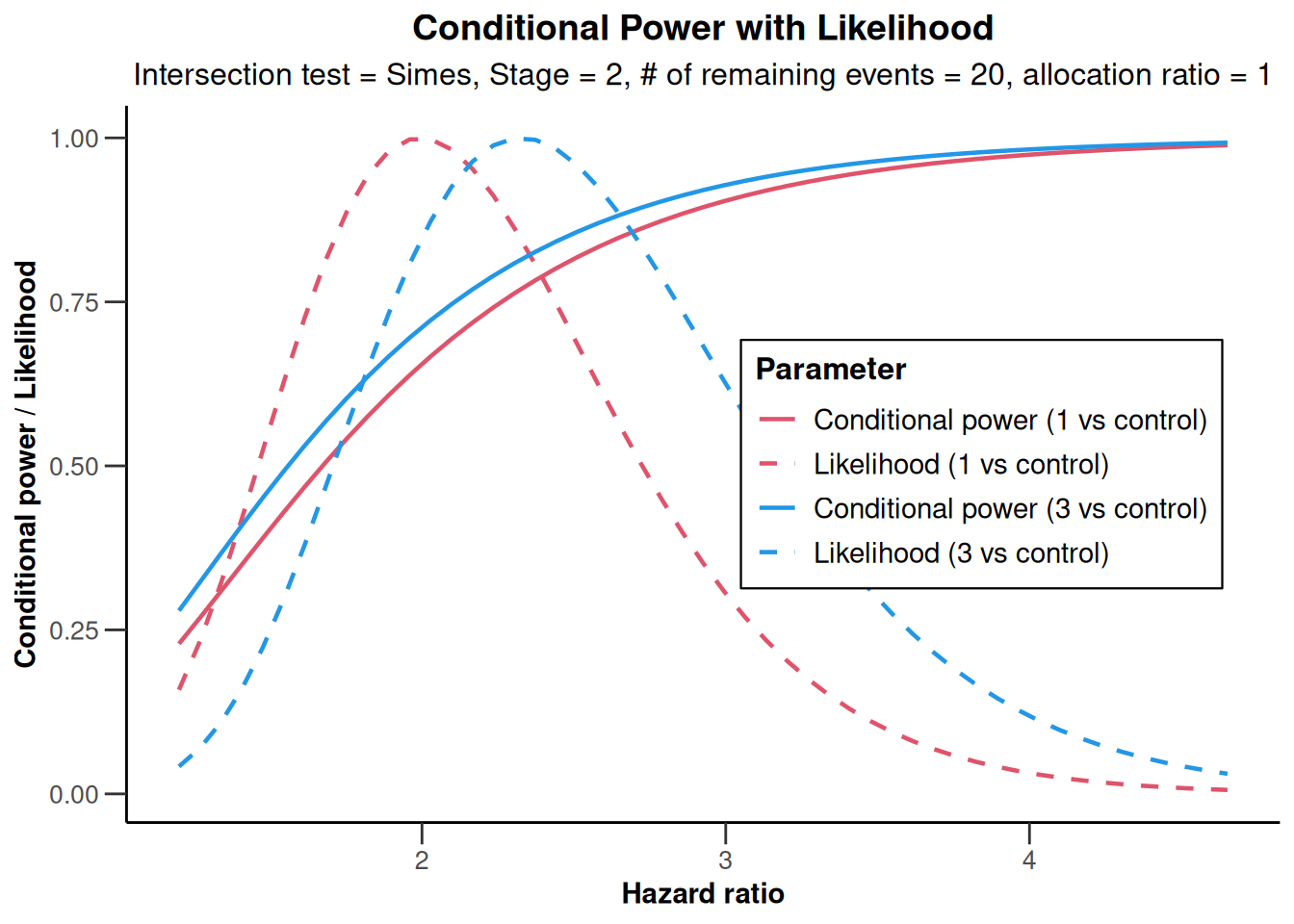
plot(analysisResultsSurvival, nPlanned = 20)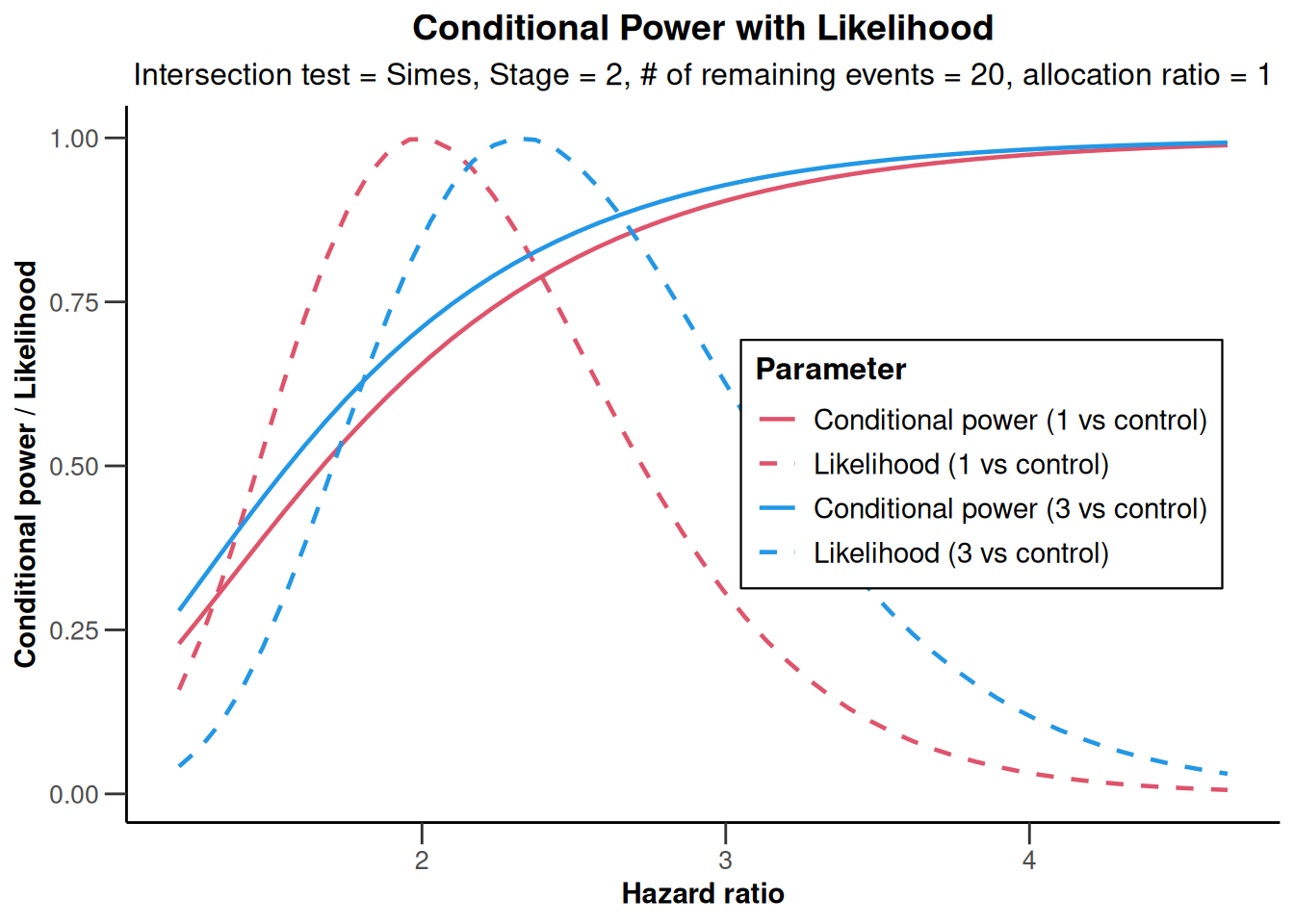
plot(analysisResultsSurvival, type = 2)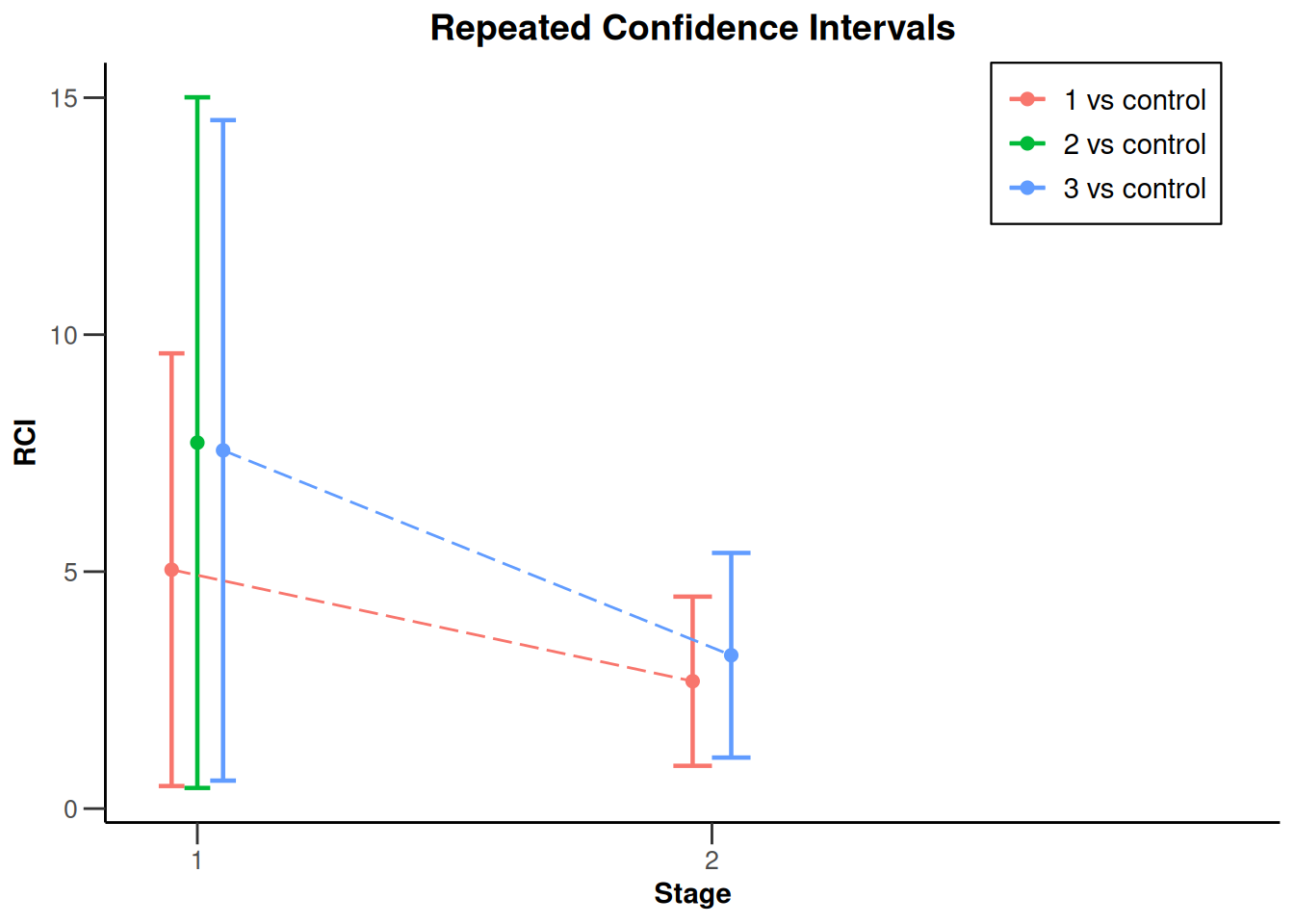
Analysis results enrichment
Analysis results enrichment - means
S1 <- getDataset(
sampleSize1 = c(14, 22, NA),
sampleSize2 = c(11, 18, NA),
mean1 = c(68.3, 107.4, NA),
mean2 = c(100.1, 140.9, NA),
stDev1 = c(124.0, 134.7, NA),
stDev2 = c(116.8, 133.7, NA)
)
S2 <- getDataset(
sampleSize1 = c(12, NA, NA),
sampleSize2 = c(18, NA, NA),
mean1 = c(107.7, NA, NA),
mean2 = c(125.6, NA, NA),
stDev1 = c(128.5, NA, NA),
stDev2 = c(120.1, NA, NA)
)
S3 <- getDataset(
sampleSize1 = c(17, 24, NA),
sampleSize2 = c(14, 19, NA),
mean1 = c(64.3, 101.4, NA),
mean2 = c(103.1, 170.4, NA),
stDev1 = c(128.0, 125.3, NA),
stDev2 = c(111.8, 143.6, NA)
)
F <- getDataset(
sampleSize1 = c(83, NA, NA),
sampleSize2 = c(79, NA, NA),
mean1 = c(77.1, NA, NA),
mean2 = c(142.4, NA, NA),
stDev1 = c(163.5, NA, NA),
stDev2 = c(120.6, NA, NA)
)
dataInput <- getDataset(S1 = S1, S2 = S2, S3 = S3, F = F)
dataInput <- getDataset(S1 = S1, S2 = S2, S12 = S3, R = F)
design <- getDesignInverseNormal(
kMax = 3, alpha = 0.025, typeOfDesign = "OF",
informationRates = c(0.2, 0.7, 1)
)
x <- getAnalysisResults(
design = design,
dataInput = dataInput,
directionUpper = FALSE,
nPlanned = 200
)
plot(x, populations = c(1, 3))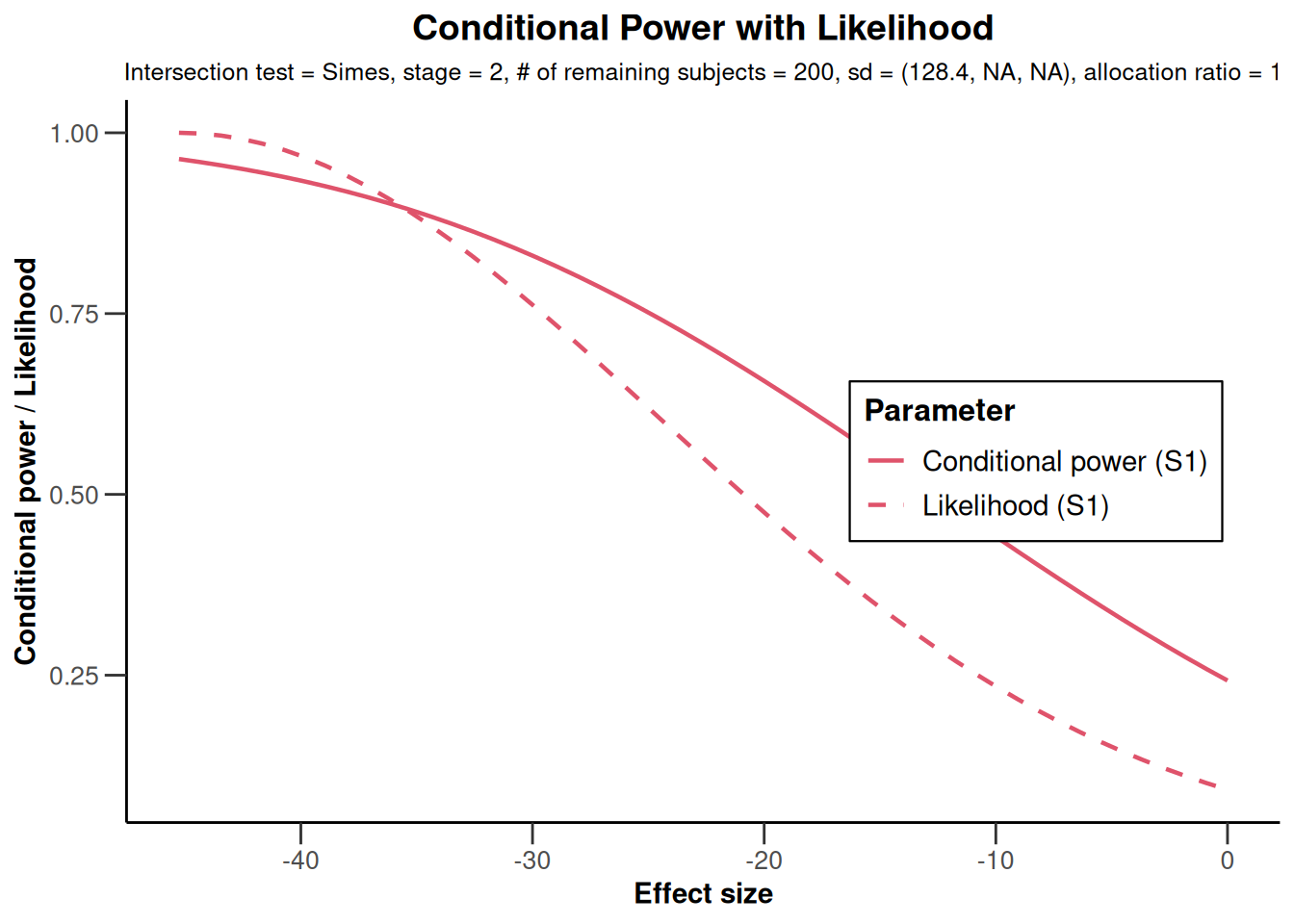
plot(x, populations = c(3))
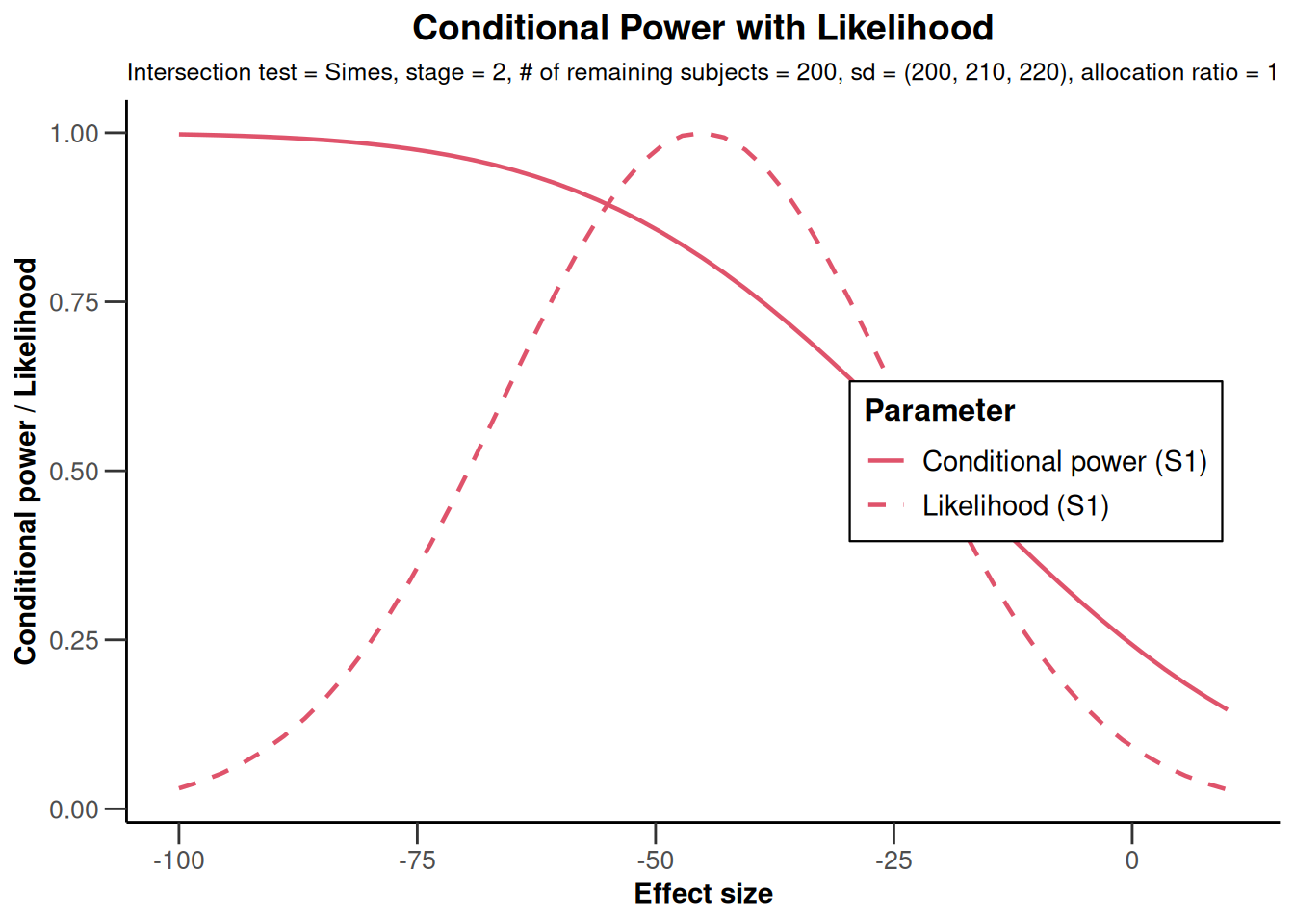
plot(x,
thetaRange = c(-100, 10),
assumedStDevs = c(200, 210, 220)
)
plot(x, type = 2)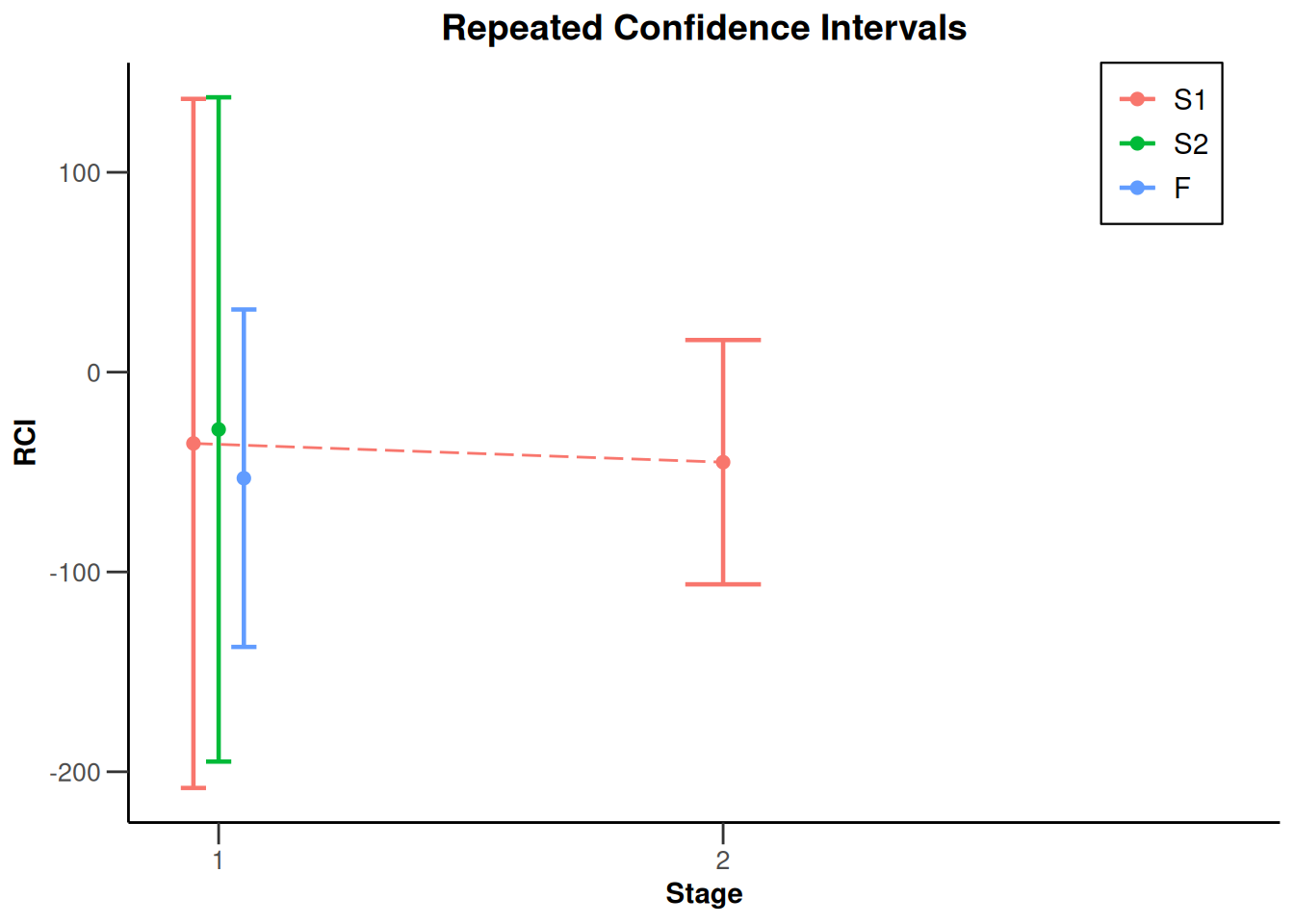
Analysis results enrichment - rates
library(rpact)
S <- getDataset(
events2 = c(3, 4),
events1 = c(7, 11),
n2 = c(30, 31),
n1 = c(33, 31)
)
R <- getDataset(
events2 = c(5, 7),
events1 = c(10, 13),
n2 = c(32, 30),
n1 = c(31, 29)
)
dataSetExampleRates <- getDataset(S1 = S, R = R)
x <- getAnalysisResults(
design = getDesignFisher(),
dataInput = dataSetExampleRates,
nPlanned = 30
)
plot(x)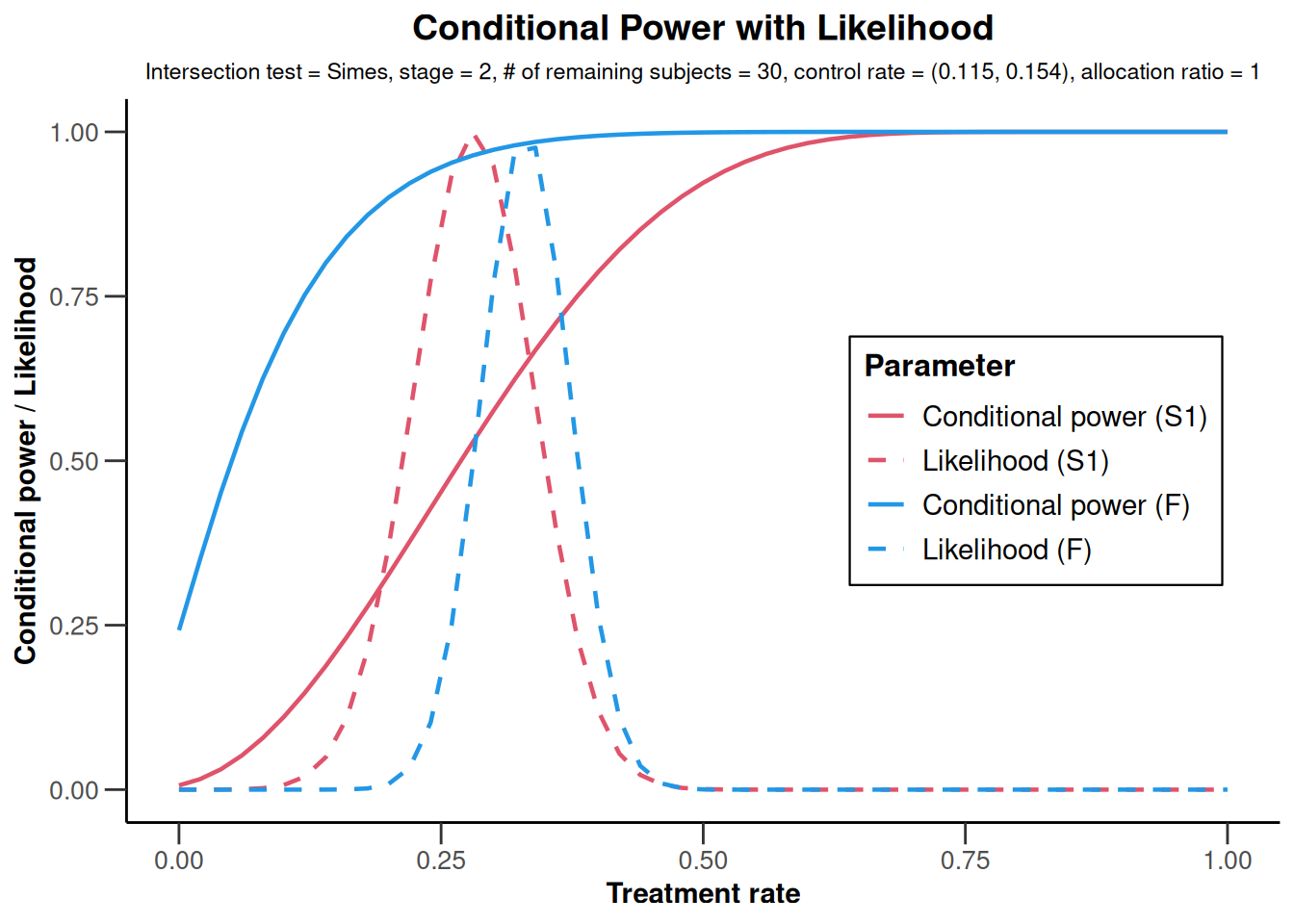
plot(x, type = 2)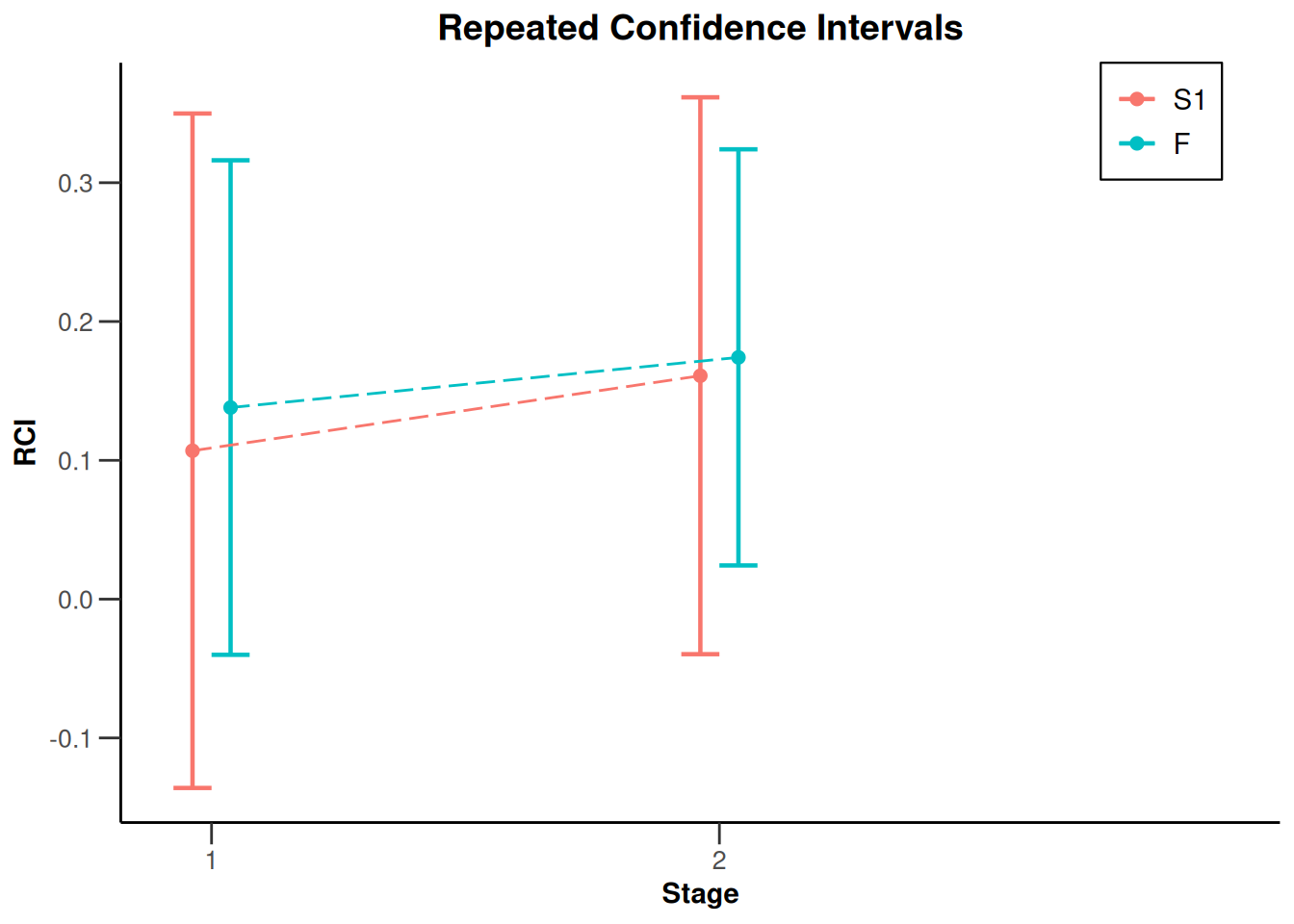
Analysis results enrichment - survival
S <- getDataset(
events = c(16, 19),
logRanks = c(1.59, 1.53)
)
F <- getDataset(
events = c(36, 59),
logRanks = c(1.98, 1.93)
)
dataSetExampleSurvival <- getDataset(S1 = S, F = F)
x <- getAnalysisResults(
design = getDesignFisher(),
dataInput = dataSetExampleSurvival,
nPlanned = 20
)Test statistics from full (and sub-populations) need to be stratified log-rank testsplot(x)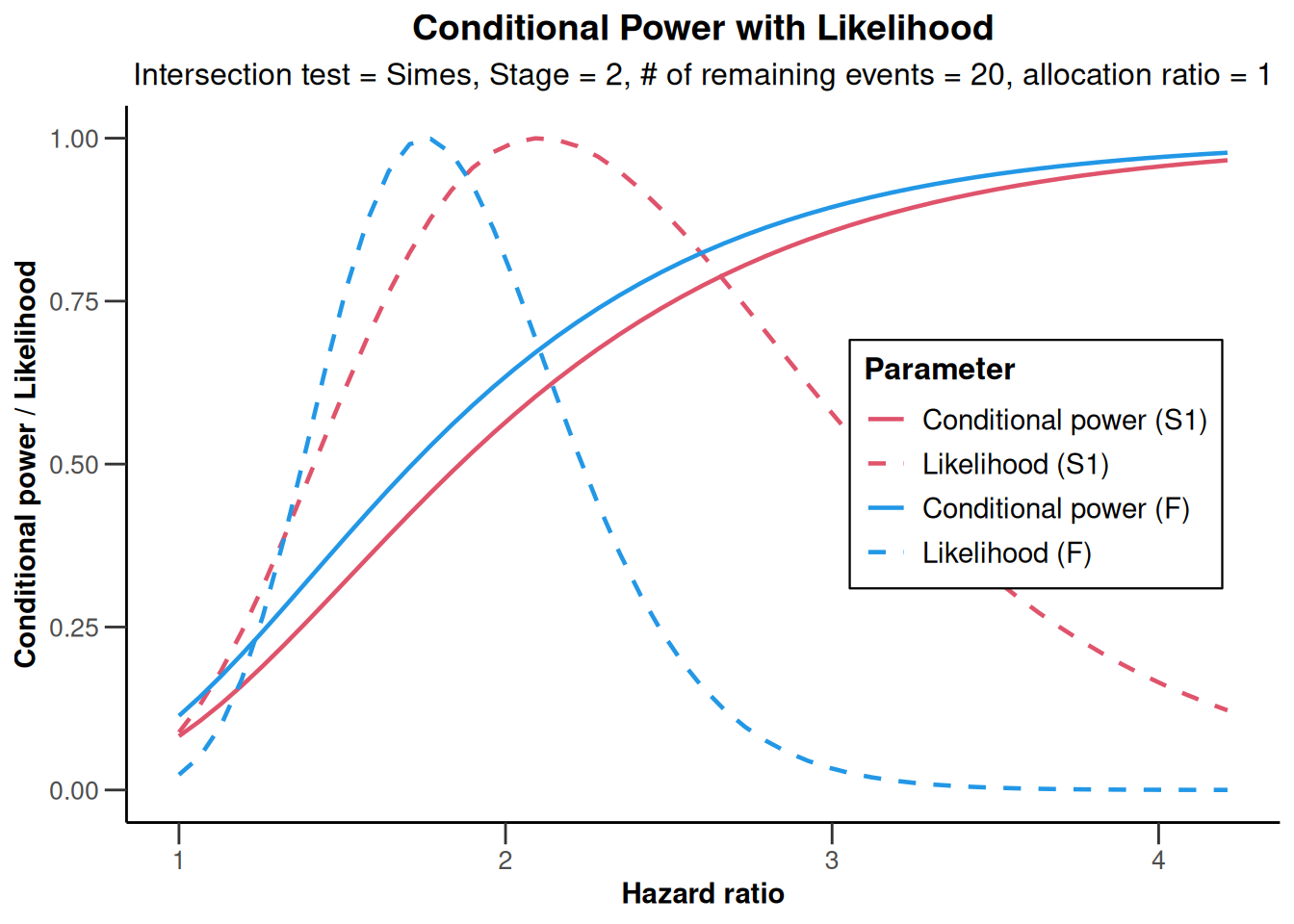
plot(x, type = 2)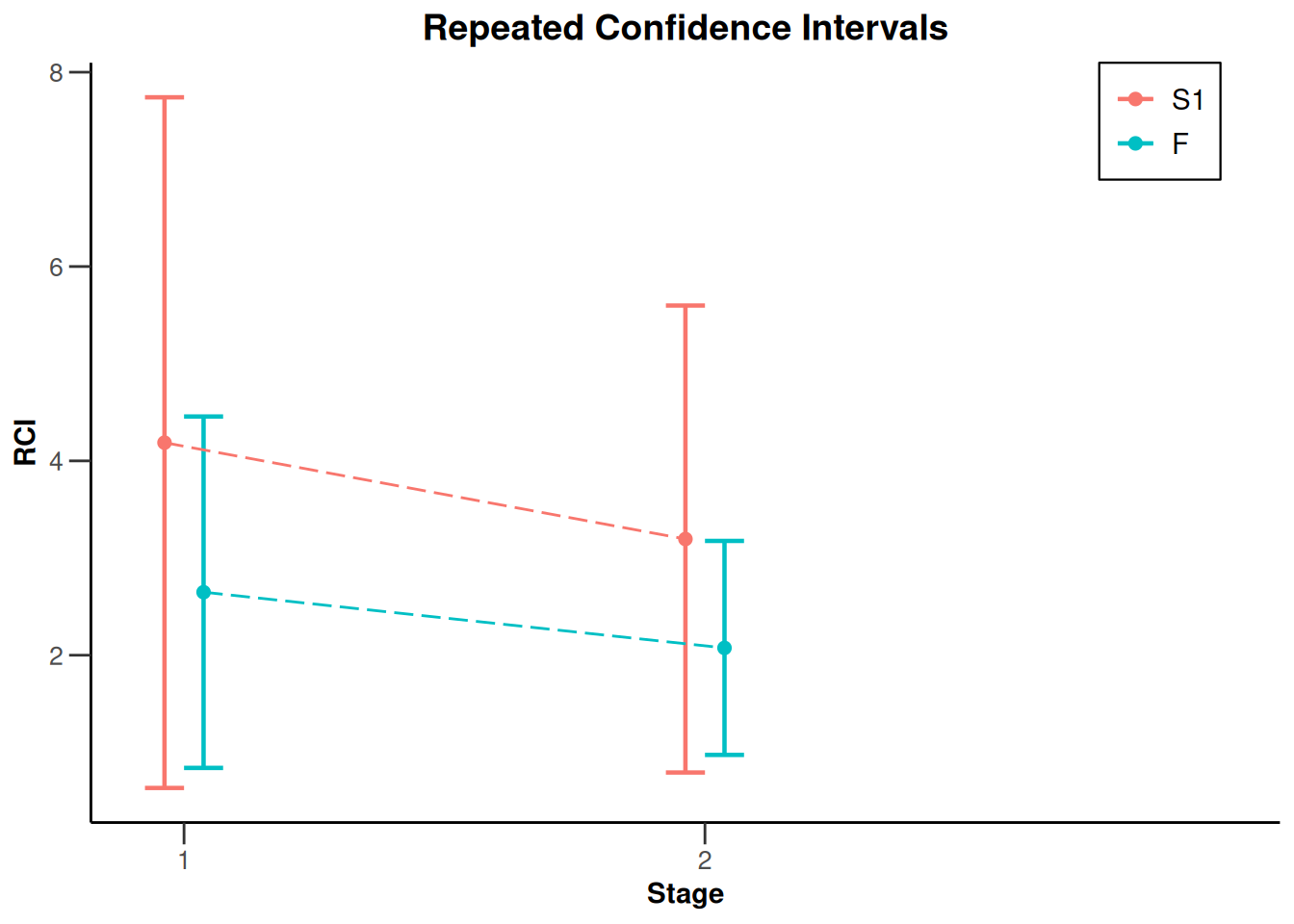
System: rpact 4.0.0, R version 4.3.3 (2024-02-29 ucrt), platform: x86_64-w64-mingw32
To cite R in publications use:
R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. To cite package ‘rpact’ in publications use:
Wassmer G, Pahlke F (2024). rpact: Confirmatory Adaptive Clinical Trial Design and Analysis. R package version 4.0.0, https://www.rpact.com, https://github.com/rpact-com/rpact, https://rpact-com.github.io/rpact/, https://www.rpact.org.