Planning and Analyzing a Group-Sequential Multi-Arm Multi-Stage Design with Binary Endpoint using rpact

Planning
Rates
Multi-arm
Analysis
This document provides an example of implementing, simulating and analyzing multi-arm-multi-stage (MAMS) designs for testing rates with rpact with special regards to futility bound determination, treatment arm selection and generic data analysis. After exemplarily using the binary endpoint analysis module from rpact, an illustrative landmark analysis (comparison of empirical survival probabilities at specific time point) using Greenwoods standard error estimation is to be performed. Since rpact itself does not directly support this type of analysis, another packages’ functionality needs to be utilized to perform the survival probability and standard error estimation to eventually use the estimates as input for a hypothetical continuous endpoint dataset which subsequently is to be analyzed as such.
Author

Stephen Schueuerhuis Gernot Wassmer Friedrich Pahlke

Published

October 28, 2024

Introduction

This document provides an exemplary implementation of multi-arm-multi-stage (MAMS) design with binary endpoint using rpact. Concretely, the vignette consists of considering design implementation with respect to futility bounds on treatment effect scale, sample size calculations and simulations given different treatment selection approaches. Further, analysis using closed testing will be performed on generic data binary and survival data.

Note that since rpact itself doesn’t support landmark analysis, i.e. comparison of survival probabilities at a fixed point in time, using the Greenwoods standard error (SE) formula. Thus the first two analyses are based on the empirical event rates only. The R packages gestate and survival are then utilized to briefly show how one could merge the packages to perform the actually intended analysis using boundaries obtained by rpact and test statistics obtained by survival probabilities and standard errors estimated using gestate and survival.

For methodological and theoretical background, refer to “Group Sequential and Confirmatory Adaptive Designs in Clinical Trials” by Gernot Wassmer and Werner Brannath.

Before starting, load the rpact package and make sure the version of the package is at least 3.1.0:

library(rpact)
packageVersion("rpact")
[1] '4.1.1'

Implementation of design

Consider we are interested in implementing a group sequential design with \(3\) stages, \(3\) treatment arms (\(2\) active, \(1\) control), \(2\) treatment arm comparisons (each active arm vs. the placebo arm), a binary endpoint, with a global one-sided \(\alpha=0.025\), and the power for each treatment arm comparison set to \(80\%\), hence \(1-\beta=0.8\). Additionally, let the critical boundaries be calculated using alpha-spending O’Brien & Fleming approach and for planning purposes, suppose equally distributed information rates. Further, non-binding futility bounds are to be set in the following way:

Considering the \(2\) active treatment arms, the goal of both arms is to confirm significant reduction in event (e.g. disease, death) rates as compared to a control arm. Thus, futility should appear exactly when there is only low reduction, no reduction or even increase seen in the data. Assume one designs a study where a treatment arm is futile in the first stage when there has only been a relative reduction of \(5\)% (i.e. rate ratio of \(0.95\)) and in the second stage when data indicates a relative reduction of \(10\)% only (i.e. rate ratio of \(0.9\)). For simplification, futility bounds are assumed to be independent. As rpact primarily uses futility bounds on \(z\)-scale, one needs to determined the \(z\)-scale value that correspond with the values listed above. Advantageously, the futility bounds on treatment effect scale are part of sample size calculation output. Therefore, rpact allows to determine the right \(z\)-value by basically examining various options for \(z\)-scale futility as input and decide on which values result in the needed treatment effect futility bounds. This can exemplarily be done by trying different \(z\)-scale futility bounds as input up until the sample size calculation command output (given certain treatment effect assumptions) indicates that the input corresponds with the desired treatment effect futility bound.

As an example on how to get the corresponding futility bound values on the different scales, see the example below:

First, one needs to initialize the design and basically take arbitrary futility bounds on \(z\)-scale as input:

# first and second stage futility on z-scale
fut1 <- 0.16
fut2 <- 0.39

d_fut <- getDesignGroupSequential(
    kMax = 3,
    alpha = 0.025,
    beta = 0.2,
    sided = 1,
    typeOfDesign = "asOF",
    informationRates = c(1 / 3, 2 / 3, 1),
    futilityBounds = c(fut1, fut2),
    bindingFutility = FALSE
)

Now, as mentioned, the sample size calculation output provides information about the futility boundaries on the treatment effect scale. Therefore, after assuming certain treatment effects, one needs to perform sample size calculation and extract the treatment effect futility bound from the respective output:

c_assum <- 0.1 # assumed rate in control
effect_assum <- 0.5 # relative reduction that is to be detected with probability of 0.8

# rates indicate binary endpoint
ssc_fut <- getSampleSizeRates(
    design = d_fut,
    riskRatio = TRUE,
    pi1 = c_assum * (1 - effect_assum),
    pi2 = c_assum
)

ssc_fut$futilityBoundsEffectScale
          [,1]
[1,] 0.9464954
[2,] 0.9085874

The values printed out above are now the futility bounds on treatment effect scale that do correspond with the values fut1 and fut2 from above. Since \(0.9465 < 0.95\) and \(0.9086 > 0.9\), the input value fut1=\(0.16\) seems to be slightly to large while fut2=\(0.39\) seems to be slightly to low, while this indicates how to adjust the input values such that one comes closer to the the true corresponding values.

Now, using a search algorithm or by simply trying different values, one results in futility bounds on \(z\)-scale summarized in the following table created using knitr:

First stage Second stage
Orig. treatment effect scale 0.950 0.900
Approx. z-Value for given t-Value 0.149 0.414
Corresponding t-scale Value 0.950 0.900
Diff. between Approx. and Input 0.000 0.000

In the table above, the Orig. treatment effect scale is the intended futility bound on treatment effect scale, Approx. \(z\)-value denotes the corresponding \(z\)-scale value approximation and Corresponding \(t\)-scale Value the actual \(t\)-scale value using the calculated approx. \(z\)-values as input.. One can see that the first stage futility bound on \(z\)-scale should approximately be chosen as \(0.14915\) and the second stage \(z\)-scale futility bound as \(0.41381\), resulting in the desired futility bound on treatment effect scale of approximately 0.95 in first and 0.9 in second stage, respectively. In the next chapter containing the sample size calculations, the respective outputs validate that these \(z\)-scale futility bounds are a reasonable choice.

Now that (approximate) futility bounds on \(z\)-scale are known, the above specified design can be entirely initialized, kMax=3 indicates a study design of three stages.

# GSD with futility bounds according to above calculations
d <- getDesignGroupSequential(
    kMax = 3,
    alpha = 0.025,
    beta = 0.2,
    sided = 1,
    typeOfDesign = "asOF",
    informationRates = c(1 / 3, 2 / 3, 1),
    futilityBounds = c(0.149145, 0.41381),
    bindingFutility = FALSE
)
d |> summary()

Sequential analysis with a maximum of 3 looks (group sequential design)

O’Brien & Fleming type alpha spending design, non-binding futility, one-sided overall significance level 2.5%, power 80%, undefined endpoint, inflation factor 1.0833, ASN H1 0.8652, ASN H01 0.843, ASN H0 0.6133.

Stage 1 2 3
Planned information rate 33.3% 66.7% 100%
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative power 0.0213 0.4471 0.8000
Futility probabilities under H1 0.062 0.011

Simply printing out the defined object gives a nice overview of all relevant design parameters. Note that the adjusted \(\alpha\) of the last stage (\(=0.0231\)) is slightly lower that the predefined global \(\alpha\), corresponding to a critical values of \(1.993\) being slightly larger than \(1.96\), which is due to alpha-spending O’Brien Fleming adjustment. Further, the output basically provides an overview of the input parameters.

Sample size calculation

When it comes to sample size calculations for designs with binary endpoints, rpact provides the command getSampleSizeRates(). It should be noted upfront that the sample size calculation in rpact always only refers to only one treatment arm comparison.

The sample size calculations code applicable here has already been indirectly used to properly determine the \(z\)-scale futility boundaries whenever futility boundaries are only given on treatment effect scale. However, this sections’ purpose now is to provide some more detail on sample size calculations in MAMS-designs with binary endpoint.

Suppose the treatment effect under \(H_0\) is \(0\) or there is even a rate increase in active treatment group, meaning the difference \(\pi_1-\pi_2 \geq 0\), with \(\pi_1\) representing the assumed event rate in the treatment group and \(\pi_2\) being the assumed event rate in the reference/control group. Again, let the parameter setting be given as above and assume an expected relative reduction of event occurrence of \(50\%\) given \(\pi_2 = 0.1\) (hence \(\pi_2 = 0.1*0.5=0.05\)). Since we are interested in directly comparing risks, we set riskRatio to TRUE which particularly results in testing \(H_0: \frac{\pi_1}{\pi_2} \geq 1\) against \(H_1:\frac{\pi_1}{\pi_2} < 1\). The sample size per stage for one treatment arm comparison can then be calculated using the commands:

c_rate <- 0.1 # assumed rate in control
effect <- 0.5 # relative reduction that is to be detected with probability of 0.8

# rates indicate binary endpoint
d_sample <- getSampleSizeRates(
    design = d,
    riskRatio = TRUE,
    pi1 = c_rate * (1 - effect),
    pi2 = c_rate
)
d_sample |> summary()

Sample size calculation for a binary endpoint

Sequential analysis with a maximum of 3 looks (group sequential design), one-sided overall significance level 2.5%, power 80%. The results were calculated for a two-sample test for rates (normal approximation), H0: pi(1) / pi(2) = 1, H1: pi(1) = 0.05, control rate pi(2) = 0.1.

Stage 1 2 3
Planned information rate 33.3% 66.7% 100%
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Efficacy boundary (t) 0.061 0.476 0.643
Futility boundary (t) 0.950 0.903
Cumulative power 0.0213 0.4471 0.8000
Number of subjects 313.8 627.5 941.3
Expected number of subjects under H1 751.7
Overall exit probability (under H0) 0.5594 0.1828
Overall exit probability (under H1) 0.0838 0.4366
Exit probability for efficacy (under H0) 0.0001 0.0059
Exit probability for efficacy (under H1) 0.0213 0.4258
Exit probability for futility (under H0) 0.5593 0.1769
Exit probability for futility (under H1) 0.0625 0.0108

Legend:

  • (t): treatment effect scale

The variable Futility boundary (t) represents the futility bounds transferred to treatment effect scale. Therefore, one can see that the predefined bounds calculated above correspond with a rate ratio of \(0.950\) at the first stage (i.e. relative reduction of \(5\%\)) and a rate ratio of \(0.903\) at the second (i.e. relative reduction of approx. \(10\%\)), being actually pretty close to the intended ones. The slight differences to the results above, again, are due to assumed independence (i.e. futility bound calculations for the different stages are done on an independent basis). However, even using this simplification, results are equivalent with a precision of \(3\) digits or more.

Another important information provided by the output is that to achieve the desired study characteristics, such as keeping the \(\alpha\)-error controlled at \(0.025\) while obtaining power of \(1-\beta = 0.8\), approx. \(\frac{314}{2}=157\) study subjects are needed per arm per stage given equally spread information rates. Thus, one results in a maximum of \(3*3*157=1413\) subjects in case one assumes a design with \(3\) treatment arms, \(2\) being active and \(1\) being a control . Multiplications by \(3\) are then due to having \(3\) stages and \(2\) active treatment arms compared to \(1\) control arm. It should be noted here that this is just an approximation of the sample size needed to achieve a power of \(1-\beta=0.8\), while power here is defined as the probability of successfully detecting the assumed effect. Simulations in following chapters will indicate that this rather rough approximate sample size is actually rather conservative since the studies appear to be overpowered in simulations, while the term power has a different meaning here: when considering simulations of studies with multiple active treatment arms, power is referred to as the probability to claim success of at least one active treatment arm in the study.

The row Exit probability for futility indicates the rather low probability of early stopping due to futility (\(1\). stage: \(0.0625\), \(2\). stage: \(0.108\)), while this depends on the assumed treatment effects and the defined boundaries. Efficacy boundary (t), just as Efficacy boundary (z-value scale) shows that an enormous decrease in events needs to be detected in the treatment group in order to reject \(H_0\) in the first stage (rate ratio of \(0.061\), i.e. relative reduction of \(1-0.061=0.939\)) which, again reflects the “conservatism” of alpha-spending O’Brien Fleming approach in early stages, however resulting in rather liberal and monotonically decreasing boundaries along the stages.

# boundary plots
par(mar = c(4, 4, .1, .1))
plot(d_sample, main = paste0(
    "Boundaries against stage-wise ",
    "cumul. sample sizes - 1"
), type = 1)
plot(d_sample, main = paste0(
    "Boundaries against stage-wise ",
    "cumul. sample sizes - 2"
), type = 2)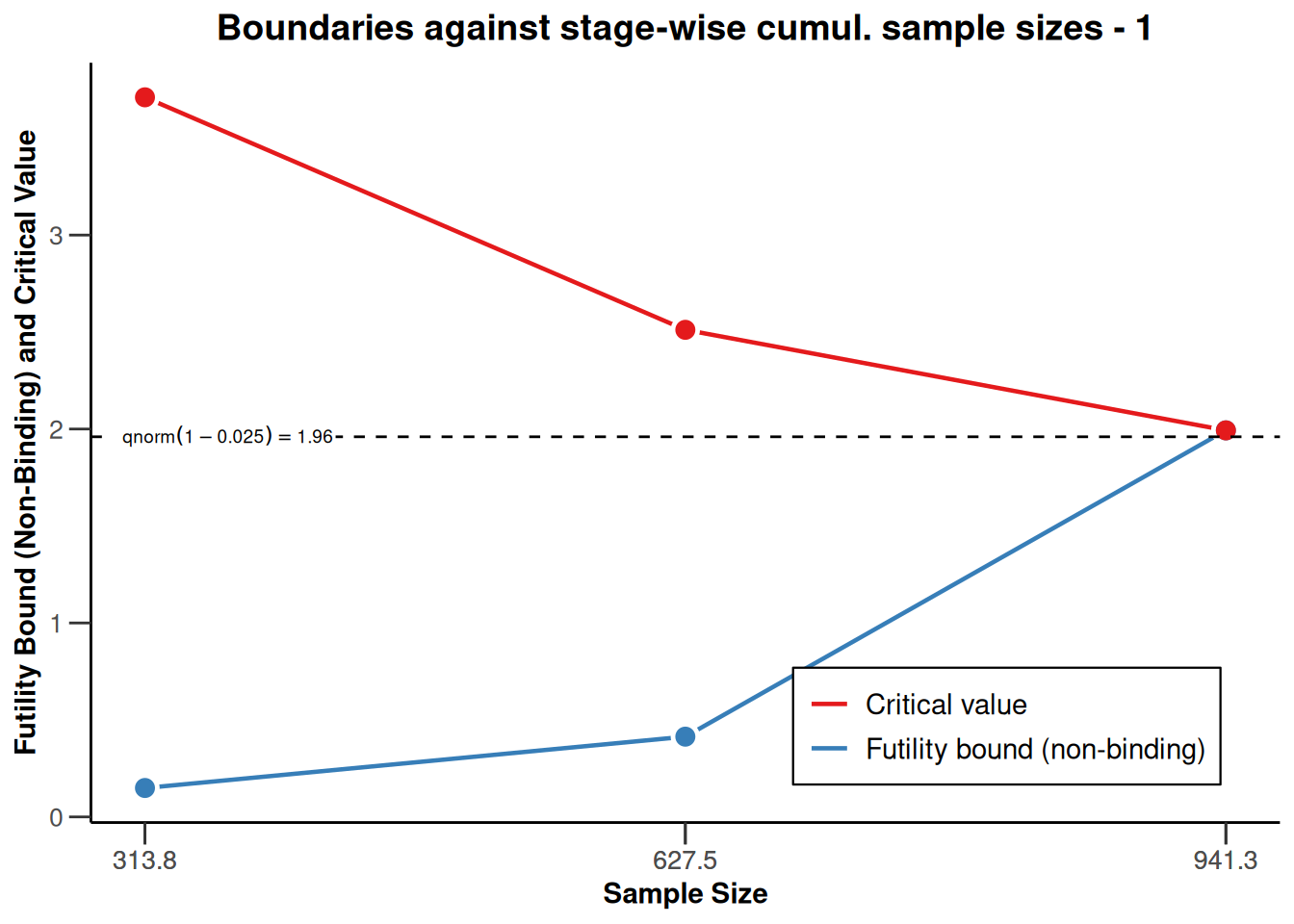

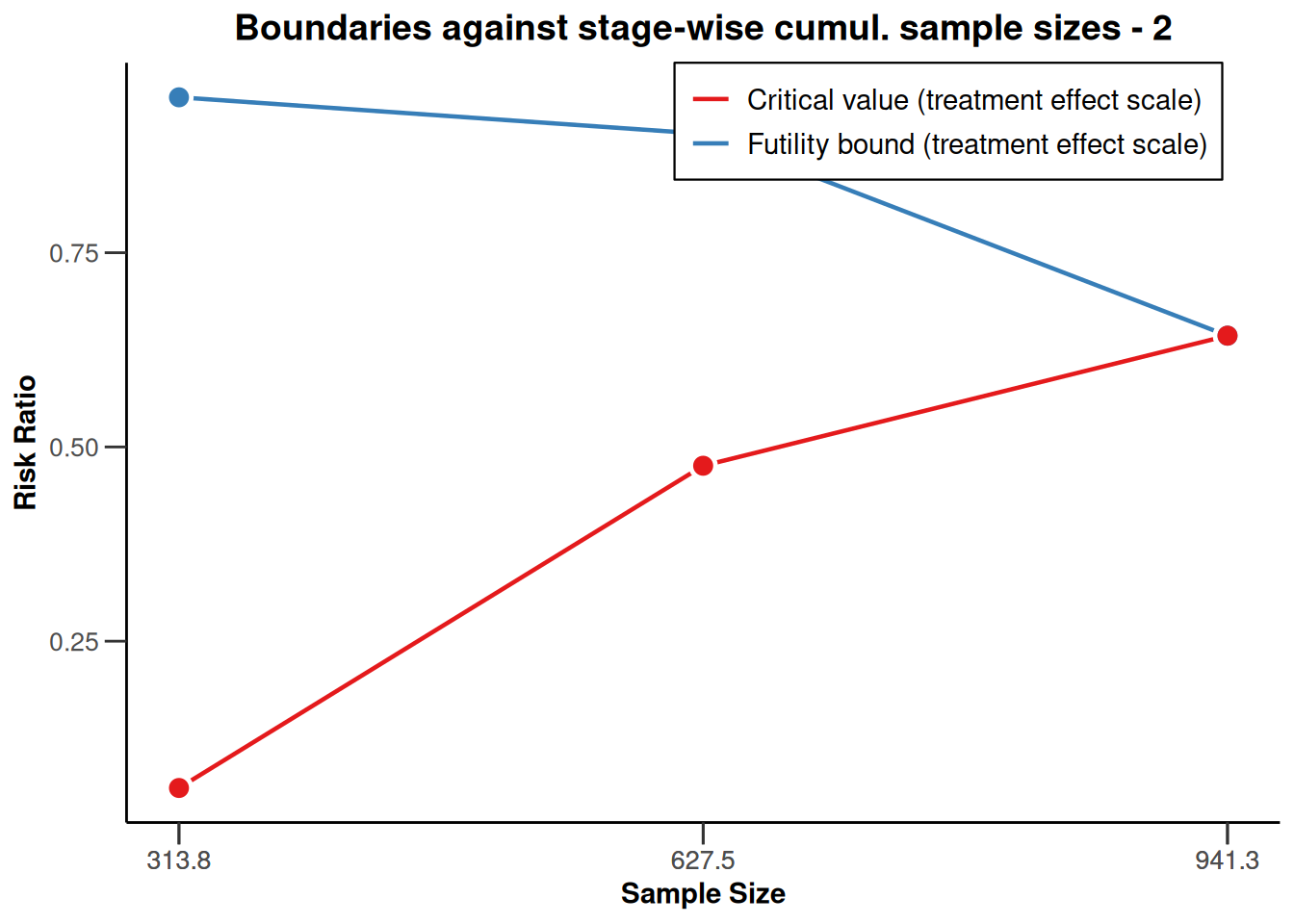
Plotting the cumulative sample size against the applicable boundaries is a way of nicely visualizing these important study characteristics. On the left plot, one can see a plot having the boundaries on the y-axis on \(z\)-scale.. The dashed line represents the critical value of a fixed study design with one-sided testing and \(\alpha=0.025 \,\) (\(\Phi^{-1}(1-\alpha) \approx 1..96\), \(\Phi\) denoting the cumulative distribution function of the standardnormal distribution, \(\Phi^{-1}\) the corresponding quantile function). The right plot basically contains the same information, while the y-axis is now given on treatment effect scale. The red line represents the efficacy bound which needs to be crossed to obtain statistical significance at the applicable stage, the blue line represents the futility bounds. Note that the plot again indicates that low risk ratio values are desirable.

Study simulations

Performing simulations prior to conducting the study is often reasonable since they allow for evaluating characteristics, such as power (please refer to definition above), assuming different scenarios or constellations of treatment effects. Thus, simulations enable to get a more holistic view on how and where the planned study could go in case the assumptions appear to be (approximately) true.

Simulation of the study design will be done using the function getSimulationMultiArmRates(), which needs an Inverse Normal Design as input, similarly defined, with the add-on of containing information about how the analysis in the simulations should be performed:

# design as above, just as inverse normal
d_IN <- getDesignInverseNormal(
    kMax = 3,
    alpha = 0.025,
    beta = 0.2,
    sided = 1,
    typeOfDesign = "asOF",
    informationRates = c(1 / 3, 2 / 3, 1),
    futilityBounds = c(0.149145, 0.41380800),
    bindingFutility = FALSE
)

To perform study simulations for instance for power or probability-of-success evaluation, one need to assume (different) effect rates in the \(2\) active treatment arms, which need to be defined in a matrix-object. For binary data, die effectMatrix refers to the actual event rate in each arm, but not to the the difference in event rates between control and active treatment arms. Further, number of iterations needs to be defined in advance.

# set number of iterations to be used in simulation
maxNumberOfIterations <- 100 # 10000

# specify the scenarios, nrow: number of scenarios, ncol: number of treatment arms
effectMatrix <- matrix(c(0.100, 0.100, 0.05, 0.05, 0.055, 0.045),
    byrow = TRUE, nrow = 3, ncol = 2
)

# first column: first treatment arm, second column: second treatment arm
show(effectMatrix)
      [,1]  [,2]
[1,] 0.100 0.100
[2,] 0.050 0.050
[3,] 0.055 0.045

Considering a design with \(2\) active treatment arms, both to be compared against a control arm, the effect matrix contains treatment effect in the first active arm in the first column and the effect in the second active arm in the second column respectively.

Next step would be to actually perform the simulation. Several variables need to be initialized in order to individualize the simulation according to the specific needs. Choosing typeOfShape as userDefined refers to the above defined effect matrix, however, one could also assume a linear relationship and initialize a vector of maximal assumed effects (piMaxVector) in treatment groups. When some functional form of dose response curve are used, it should be noted that the piMaxVector may be used as the maximum treatment effect on the whole dose response curve instead of observed dose range, which could be misleading. Therefore it is suggested to use the userDefined shape. directionUpper is set to FALSE since low obtained rates of events do correspond with a better clinical outcome and reducing the rate is considered beneficial to the subjects. Intersection test to be performed is Simes , while other options would be given by e.g. Bonferroni or Dunnett, with Dunnett being the default setting. typeOfSelection is initially set to rbest with rValue being 2, which means that at each stage, the \(2\) best treatment arms should be carried forward. successCriterion = "all" means that to stop the study early due to efficacy, both active treatment arms need to be tested significantly at interim analysis and another option would be to set successCriterion = "atLeastOne" to declare significant testing of one treatment arm to be sufficient for study success at interim. The vector plannedSubjects contains the cumulative per arm per stage sample sizes previously calculated.

# first simulation
simulation <- getSimulationMultiArmRates(
    design = d_IN,
    activeArms = 2,
    effectMatrix = effectMatrix,
    typeOfShape = "userDefined",
    piControl = 0.1,
    intersectionTest = "Simes",
    directionUpper = FALSE,
    typeOfSelection = "rBest",
    rValue = 2,
    effectMeasure = "testStatistic",
    successCriterion = "all",
    plannedSubjects = c(157, 314, 471),
    allocationRatioPlanned = 1,
    maxNumberOfIterations = maxNumberOfIterations,
    seed = 145873,
    showStatistics = TRUE
)
simulation |> summary()

Simulation of a binary endpoint (multi-arm design)

Sequential analysis with a maximum of 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were simulated for a multi-arm comparisons for rates (2 treatments vs. control), H0: pi(i) - pi(control) = 0, power directed towards smaller values, H1: pi_max as specified, control rate pi(control) = 0.1, planned cumulative sample size = c(157, 314, 471), effect shape = user defined, intersection test = Simes, selection = r best, r = 2, effect measure based on test statistic, success criterion: all, simulation runs = 100, seed = 145873.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Reject at least one [1] 0.0200
Reject at least one [2] 0.7900
Reject at least one [3] 0.9200
Rejected arms per stage [1]
Treatment arm 1 0 0 0.0100
Treatment arm 2 0 0 0.0100
Rejected arms per stage [2]
Treatment arm 1 0 0.4000 0.3200
Treatment arm 2 0 0.3200 0.3900
Rejected arms per stage [3]
Treatment arm 1 0 0.3100 0.3900
Treatment arm 2 0.0100 0.4800 0.3800
Success per stage [1] 0 0 0
Success per stage [2] 0 0.2600 0.3800
Success per stage [3] 0 0.2800 0.3700
Stage-wise number of subjects [1]
Treatment arm 1 157.0 157.0 157.0
Treatment arm 2 157.0 157.0 157.0
Control arm 157.0 157.0 157.0
Stage-wise number of subjects [2]
Treatment arm 1 157.0 157.0 157.0
Treatment arm 2 157.0 157.0 157.0
Control arm 157.0 157.0 157.0
Stage-wise number of subjects [3]
Treatment arm 1 157.0 157.0 157.0
Treatment arm 2 157.0 157.0 157.0
Control arm 157.0 157.0 157.0
Expected number of subjects under H1 [1] 711.2
Expected number of subjects under H1 [2] 1229.3
Expected number of subjects under H1 [3] 1243.4
Overall exit probability [1] 0.6300 0.2300
Overall exit probability [2] 0.0600 0.2700
Overall exit probability [3] 0.0400 0.2800
Selected arms [1]
Treatment arm 1 1.0000 0.3700 0.1400
Treatment arm 2 1.0000 0.3700 0.1400
Selected arms [2]
Treatment arm 1 1.0000 0.9400 0.6700
Treatment arm 2 1.0000 0.9400 0.6700
Selected arms [3]
Treatment arm 1 1.0000 0.9600 0.6800
Treatment arm 2 1.0000 0.9600 0.6800
Number of active arms [1] 2.000 2.000 2.000
Number of active arms [2] 2.000 2.000 2.000
Number of active arms [3] 2.000 2.000 2.000
Conditional power (achieved) [1] 0.0614 0.1061
Conditional power (achieved) [2] 0.3845 0.5980
Conditional power (achieved) [3] 0.4098 0.7031
Exit probability for efficacy 0.0213 0.4258
Exit probability for futility [1] 0.6300 0.2300
Exit probability for futility [2] 0.0600 0.0100
Exit probability for futility [3] 0.0400 0

Legend:

  • (i): treatment arm i
  • [j]: effect matrix row j (situation to consider)

In this output, the different input situations are indicated through \([\,j\,]\) while \(j=1,2,3\).

Under \(H_0\) with assumed treatment effect equal to the assumed effect in the control group (scenario 1), probability of rejecting at least one is low (i.e. committing type I error, Reject at least one [1] \(= 0.0181\)), while rejection probability (under alternative power) is high especially assuming high treatment effects in both treatment arms (under alternative, Reject at least one [2] \(= 0.8550\) for scenario \(2\)). Note also that, in any case, both treatment arms are selected as rValue=2 means that the two best treatment arms (i.e. all arms in this case) are selected, regardless of if the one or both treatment arms meet the applicable futility bounds. Further, the simulation output contains several information. That is, e.g. stage-wise number of subjects are calculated and probabilities for arms to be selected in each stage are provided for each assumed effect. Additionally, expected sample size, which is commonly used as optimality criterion of designs, stopping due to futility-probabilities and conditional power, defined as the probability of having a statistically significant result given the data observed thus far, are listed. Note that, since probability of futility stop is rather high in scenario \(1\) (first stage: \(0.5797\), second stage: \(0.1920\)), the corresponding expected number of subjects is approximately \(776\), lying far below the expected sample sizes in the other scenarios.

Stage-wise treatment arm selection

Now, suppose the underlying treatment arm selection scheme is different and especially not straightforwardly covered by the other available and pre-defined options in rpact (i.e. best, rBest, epsilon, all). Then, rpact accounts for that by allowing users to implement a user defined treatment arm selection function thus being capable of covering various different selection approaches. The user needs to set typeOfSelection to userDefined and define a function used as input for the selectArmsFunction-argument.

Say e.g. a treatment arm should be selected if and only if it doesn’t meet the futility bound, and if it does, function should be specified such that this arm is deselected at the applicable stage. See the different treatment arm selection approaches illustrated for the first stage depending on the different potential outcomes in the figures below, while the first diagram illustrates the procedure using rBest and the second using the userDefined scheme here, while the numbers represent the following potential first stage analysis results:

  1. Both active Treament Arms significant
  2. 1 active Treatment Arm significant, 1 active Treatment Arm non-significant
  3. 1 active Treatment Arm futile, 1 active Treatment Arm significant
  4. Both active Treatment Arms non-significant
  5. 1 active Treatment Arm futile, 1 active Treatment Arm non-significant
  6. Both active Treatment Arm futile

rBest, rValue=2

This first diagram graphically represent how treatment selection proceeds choosing typeOfSelection=rBest with rValue=2 in case of the study design previously defined. Early study success can be obtained whenever both treatment arms can be tested significantly at interim, continuation of study with only non-significant (meaning neither stopped for efficacy, not for futility) active treatment arms is to be done whenever one of the \(2\) active arms is discontinued due to efficacy and if none of the arms can be tested significantly at interim, the study continues with both treatment arms as even arms crossing the futility bounds are to be carried forward using rBest, rValue=2.

userDefined

This second diagram illustrates the active treatment arm selection that is to be implemented through the user defined selection function. Efficacy stop occurs when both active treatment arms are tested significantly at interim, continuation with non-significant arm only happens only when one active arm is significant while the other arm is not, but neither futile. The study also terminates early with success of one arm when one active arm is futile while the other can be deemed superior to control, continuation with non-futile arms only is done when both arms are non-significant or one of them is non-significant while the other one is futile. Lastly, futility stop can also happen at interim.

Now that the futility bounds are defined in the design specification already one could believe that selection rule is only an add-on to the futility bound. However, this is not true since specifying selection rule overwrites the futility bound as continuation-criterion for treatment arms. Thus, even if futility bounds are pre-specified, to implement stopping due to futility in application of getSimulationMultiArmRates() (but also getSimulationMultiArmMeans(), getSimulationMultiArmSurvival()), one could use these as input in the customized selection function. In this case, having the previously defined futility bounds of \(0.149145\) at the first interim and \(0.413808\) at the second respectively, there is a need to individualize the selection scheme along the different stages. It is important to note here that effectMeasure = "testStatistic" needs to be set as the futility bounds have intentionally been transformed to and calculated on \(z\)-scale. Now, rpact enables implementation of this selection scheme by allowing stage as an argument in the selection function, additional to effectVector:

# first row: first stage futility bounds, second stage: second stage futility bound
futility_bounds <- matrix(c(d_IN$futilityBounds, d_IN$futilityBounds), nrow = 2)

# selection function
selection <- function(effectVector, stage) {
    # if stage==1, compare to first stage fut. bounds,
    # if stage==2, compare to second stage fut. bounds
    selectedArms <- switch(stage,
        (effectVector >= futility_bounds[1, ]),
        (effectVector >= futility_bounds[2, ])
    )
    return(selectedArms)
}

simulation <- getSimulationMultiArmRates(
    design = d_IN,
    activeArms = 2,
    effectMatrix = effectMatrix,
    typeOfShape = "userDefined",
    piControl = 0.1,
    intersectionTest = "Simes",
    directionUpper = FALSE,
    typeOfSelection = "userDefined",
    selectArmsFunction = selection,
    effectMeasure = "testStatistic",
    successCriterion = "all",
    plannedSubjects = c(157, 314, 471),
    allocationRatioPlanned = 1,
    maxNumberOfIterations = maxNumberOfIterations,
    seed = 145873,
    showStatistics = TRUE
)
simulation |> summary()

Simulation of a binary endpoint (multi-arm design)

Sequential analysis with a maximum of 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were simulated for a multi-arm comparisons for rates (2 treatments vs. control), H0: pi(i) - pi(control) = 0, power directed towards smaller values, H1: pi_max as specified, control rate pi(control) = 0.1, planned cumulative sample size = c(157, 314, 471), effect shape = user defined, intersection test = Simes, selection = user defined, effect measure based on test statistic, success criterion: all, simulation runs = 100, seed = 145873.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Reject at least one [1] 0.0200
Reject at least one [2] 0.8200
Reject at least one [3] 0.8100
Rejected arms per stage [1]
Treatment arm 1 0 0 0.0200
Treatment arm 2 0 0 0
Rejected arms per stage [2]
Treatment arm 1 0 0.4200 0.3300
Treatment arm 2 0.0100 0.3700 0.3000
Rejected arms per stage [3]
Treatment arm 1 0.0100 0.2300 0.2800
Treatment arm 2 0.0100 0.4800 0.2900
Success per stage [1] 0 0 0.0200
Success per stage [2] 0 0.3400 0.4500
Success per stage [3] 0.0100 0.2800 0.4200
Stage-wise number of subjects [1]
Treatment arm 1 157.0 140.5 85.6
Treatment arm 2 157.0 103.3 71.4
Control arm 157.0 157.0 157.0
Stage-wise number of subjects [2]
Treatment arm 1 157.0 145.4 133.7
Treatment arm 2 157.0 147.1 122.1
Control arm 157.0 157.0 157.0
Stage-wise number of subjects [3]
Treatment arm 1 157.0 129.7 112.1
Treatment arm 2 157.0 148.5 151.4
Control arm 157.0 157.0 157.0
Expected number of subjects under H1 [1] 657.8
Expected number of subjects under H1 [2] 1121.0
Expected number of subjects under H1 [3] 1106.8
Overall exit probability [1] 0.6200 0.2700
Overall exit probability [2] 0.0500 0.4100
Overall exit probability [3] 0.0800 0.3600
Selected arms [1]
Treatment arm 1 1.0000 0.3400 0.0600
Treatment arm 2 1.0000 0.2500 0.0500
Selected arms [2]
Treatment arm 1 1.0000 0.8800 0.4600
Treatment arm 2 1.0000 0.8900 0.4200
Selected arms [3]
Treatment arm 1 1.0000 0.7600 0.4000
Treatment arm 2 1.0000 0.8700 0.5400
Number of active arms [1] 2.000 1.553 1.000
Number of active arms [2] 2.000 1.863 1.630
Number of active arms [3] 2.000 1.772 1.679
Conditional power (achieved) [1] 0.0627 0.5144
Conditional power (achieved) [2] 0.4522 0.7123
Conditional power (achieved) [3] 0.4165 0.7539
Exit probability for efficacy 0.0213 0.4258
Exit probability for futility [1] 0.6200 0.2700
Exit probability for futility [2] 0.0500 0.0700
Exit probability for futility [3] 0.0700 0.0800

Legend:

  • (i): treatment arm i
  • [j]: effect matrix row j (situation to consider)

Depending on what stage the simulation is currently iterating through, the switch() in the treatment selection function recognizes the stage changes and adapts the applicable futility bound by switching rows in the predefined futility bound matrix.

Again, assuming \(H_0\) to be true, the probability of falsely rejecting it is \(0.0181\), thus this simulation again indicates type I error rate control at \(\alpha=0.025\). The power assuming a \(50\%\) reduction is given through \(0.8304\). Since now, stopping of treatment arms is determined by crossing the futility bounds or not, the probability of having futility in the first stage increases to \(0.5968\) in the first and to \(0.2984\) in the second stage under \(H_0\) as compared to the first simulation. Having a different treatment selection scheme also result in lower expected number of subjects and, in opposite to the first simulation, the number of arms per scenario lies \(<2\) starting from stage \(2\) since this treatment selection allows for early discontinuation of study arms whereas in the first simulation, arms are to be carried forward regardless of potential futility.

In both simulations, with initially calculated 157 subjects per arm per stage and a relative event rate reduction of \(50\%\) as alternative, one can see that the study is overpowered (since Reject at least one [j]>0.8 in scenario \(2\)), which is due to the considered alternative having approximately the same effect in the two active treatment arms. For the second simulation, performing simulations through different potentially optimal sample sizes (in a sense that being the smallest sample size needed to achieve \(80\%\) power) indicate that one could save some subjects and still achieve the desired power. The following plot shows the minimum sample size that one could choose to achieve the power requirements, which appears to be about \(146\), however, one should keep in mind that this number might slightly be deviating from an analytically optimal solution due to deviations introduced by the simulation:

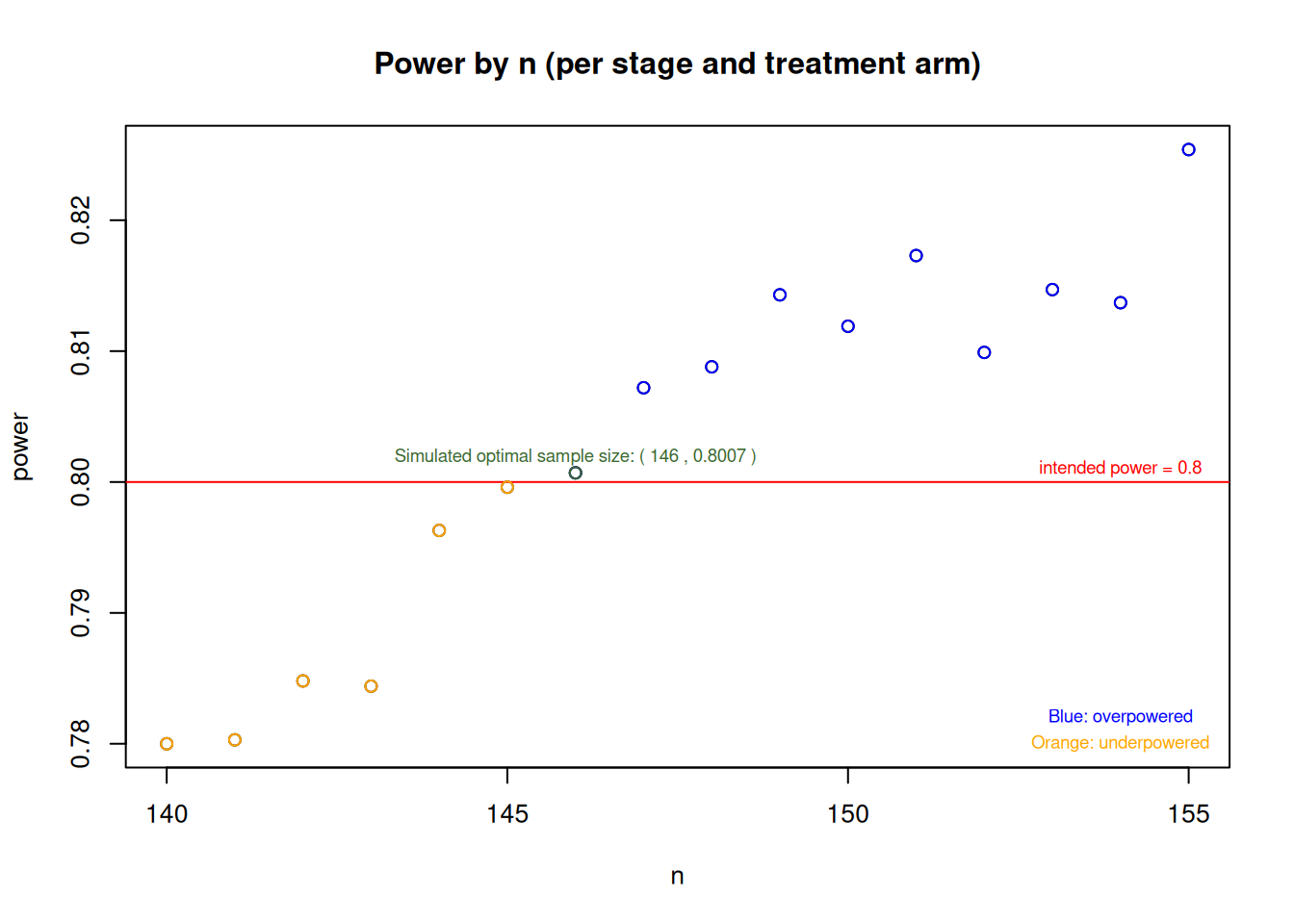
Further, it should be noted here that even if one explicitly has \(\pi_2=0..1\) under the null hypothesis, testing the hypothesis \(H_0: \frac{\pi_1}{\pi_2}\geq1\) means that whenever \(\pi_1\geq\pi_2\) with \(\pi_2, \, \pi_1 \in (0,1]\), one has a scenario where the null hypothesis is true. Consequently, one should properly check if the type I error rate is controlled not only assuming \(\pi_2=0.1\), but also considering the other scenarios when \(\pi_2 \neq 0.1\). For the second simulation, considering only the cases where rate equality holds, following plot obtained by simulation indicate that, given the study configurations here, the type I error rate is controlled under various control event rate assumptions:

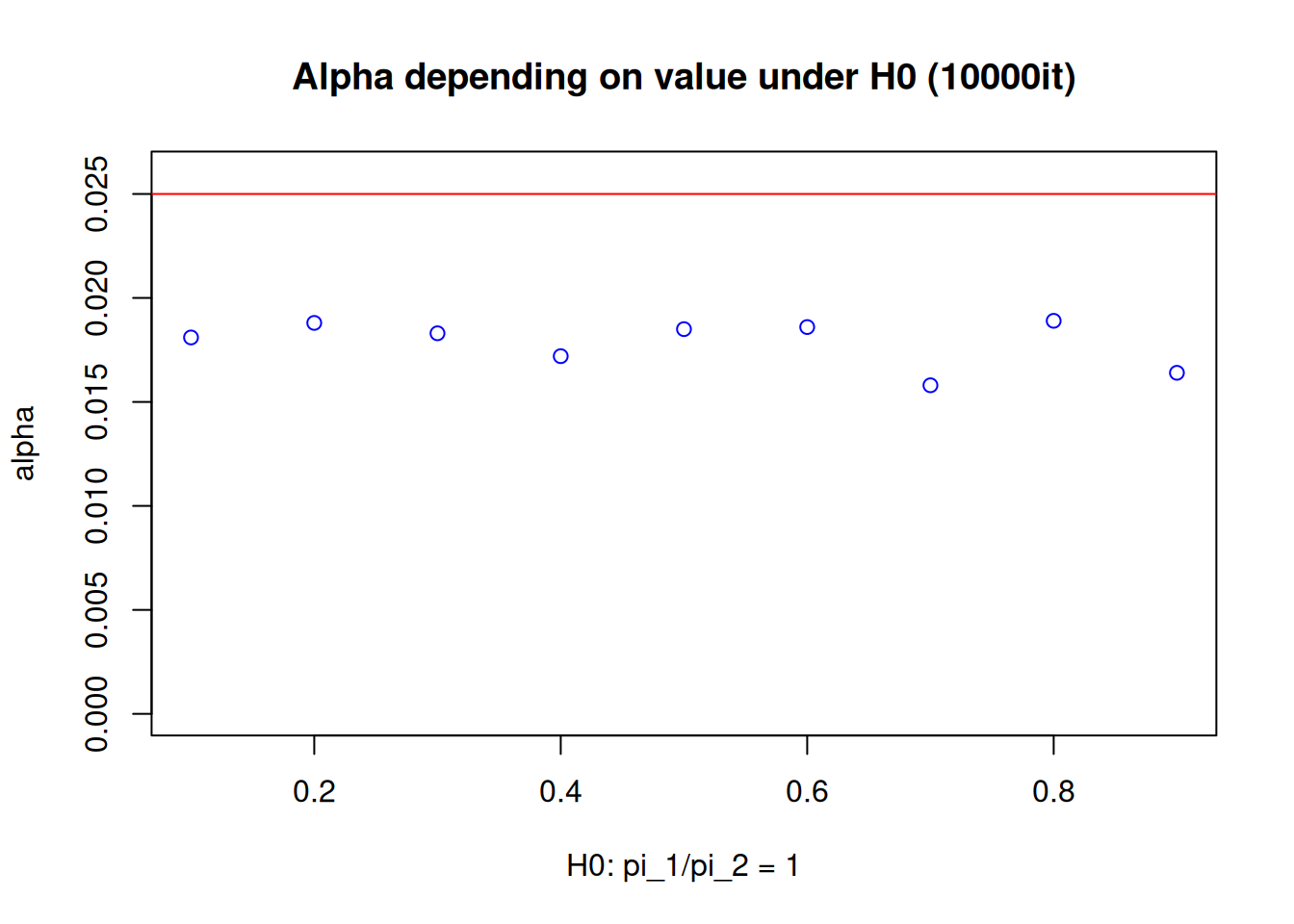
Illustrative analysis with generic Data

In the next chapters, different hypothetical binary endpoint datasets are generated and analyzed using the getAnalysisResults() command. As previously mentioned, rpact itself doesn’t support landmark analysis using the Greenwoods standard error (SE) formula. Thus the first two analyses base on the empirical event rates only. Afterwards, gestate and survival are then used to show how one could merge the packages to perform the intended analysis using boundaries obtained by rpact and test statistics obtained by survival probabilities and standard errors estimated using gestate and survival.

First theoretical path

In the first stage analysis, one first has to manually enter a dataset for data observed in the trial:

genData_1 <- getDataset(
    events1      = 4,
    events2      = 8,
    events3      = 16,
    sampleSizes1 = 153,
    sampleSizes2 = 157,
    sampleSizes3 = 156
)

genData_1 |> summary()

Dataset of multi-arm rates

The dataset contains the sample sizes and events of two treatment groups and one control group.

Stage 1 1 1
Group 1 2 3
Sample size 153 157 156
Number of events 4 8 16

This dataset is a generic realization of data from the first stage in a design with binary endpoint under the input assumption of having a \(50\%\) rate reduction in the treatment groups given \(\pi_2=0.1\). The highest index (\(3\)) corresponds with the events occurred in the control group and with the underlying sample sizes, respectively. The other indices represent active treatment groups. Data here is chosen such that one can see lower event rates in the active treatment groups. Note the slight imbalances in sample sizes, which might occur due to dropouts or recruitment issues.

Actual analysis of the first stage using Simes as intersection test goes as follows:

results_1 <- getAnalysisResults(
    design = d_IN,
    dataInput = genData_1,
    directionUpper = FALSE,
    intersectionTest = "Simes"
)
results_1 |> summary()

Multi-arm analysis results for a binary endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm test for rates, Simes intersection test, normal approximation test. H0: pi(i) - pi(control) = 0 against H1: pi(i) - pi(control) < 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) -0.076
Cumulative effect size (2) -0.052
Cumulative treatment rate (1) 0.026
Cumulative treatment rate (2) 0.051
Cumulative control rate 0.103
Stage-wise test statistic (1) -2.730
Stage-wise test statistic (2) -1.716
Stage-wise p-value (1) 0.0032
Stage-wise p-value (2) 0.0431
Adjusted stage-wise p-value (1, 2) 0.0063
Adjusted stage-wise p-value (1) 0.0032
Adjusted stage-wise p-value (2) 0.0431
Overall adjusted test statistic (1, 2) 2.493
Overall adjusted test statistic (1) 2.730
Overall adjusted test statistic (2) 1.716
Test action: reject (1) FALSE
Test action: reject (2) FALSE
Conditional rejection probability (1) 0.2907
Conditional rejection probability (2) 0.1204
95% repeated confidence interval (1) [-0.212; 0.043]
95% repeated confidence interval (2) [-0.191; 0.079]
Repeated p-value (1) 0.1150
Repeated p-value (2) 0.2429

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Although having obviously lower event rates in the first stage already, none of the \(2\) hypotheses can be rejected, which can manually be tested comparing e.g. the overall adjusted test statistics for the global intersection hypothesis of having no effect in neither one of the active treatment arms to the efficacy bound and see that \(2.493 < 3.710\), i.e. no rejection of global intersection. Neither stop due to futility appears since no futility boundary is crossed at stage \(1\), which means that both treatment arms are to be carried forward to a second stage analysis. For obtaining non-significance in stage \(1\), one could also compare repeated p-values to full \(\alpha\).

Proceeding to second stage, a generic dataset might look as follows, while the second vector entries represent second stage data:

# assuming there was no futility or efficacy stop study proceeds to randomize subjects
genData_2 <- getDataset(
    events1      = c(4, 7),
    events2      = c(8, 7),
    events3      = c(16, 15),
    sampleSizes1 = c(153, 155),
    sampleSizes2 = c(157, 155),
    sampleSizes3 = c(156, 155)
)
genData_2 |> summary()

Dataset of multi-arm rates

The dataset contains the sample sizes and events of two treatment groups and one control group. The total number of looks is two; stage-wise and cumulative data are included.

Stage 1 1 1 2 2 2
Group 1 2 3 1 2 3
Stage-wise sample size 153 157 156 155 155 155
Cumulative sample size 153 157 156 308 312 311
Stage-wise number of events 4 8 16 7 7 15
Cumulative number of events 4 8 16 11 15 31

Here, again, event rates are lower in treatment groups.

results_2 <- getAnalysisResults(
    design = d_IN,
    dataInput = genData_2,
    directionUpper = FALSE,
    intersectionTest = "Simes"
)
results_2 |> summary()

Multi-arm analysis results for a binary endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm test for rates, Simes intersection test, normal approximation test. H0: pi(i) - pi(control) = 0 against H1: pi(i) - pi(control) < 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) -0.076 -0.064
Cumulative effect size (2) -0.052 -0.052
Cumulative treatment rate (1) 0.026 0.036
Cumulative treatment rate (2) 0.051 0.048
Cumulative control rate 0.103 0.100
Stage-wise test statistic (1) -2.730 -1.770
Stage-wise test statistic (2) -1.716 -1.770
Stage-wise p-value (1) 0.0032 0.0384
Stage-wise p-value (2) 0.0431 0.0384
Adjusted stage-wise p-value (1, 2) 0.0063 0.0384
Adjusted stage-wise p-value (1) 0.0032 0.0384
Adjusted stage-wise p-value (2) 0.0431 0.0384
Overall adjusted test statistic (1, 2) 2.493 3.014
Overall adjusted test statistic (1) 2.730 3.182
Overall adjusted test statistic (2) 1.716 2.464
Test action: reject (1) FALSE TRUE
Test action: reject (2) FALSE FALSE
Conditional rejection probability (1) 0.2907 0.7911
Conditional rejection probability (2) 0.1204 0.5133
95% repeated confidence interval (1) [-0.212; 0.043] [-0.130; -0.005]
95% repeated confidence interval (2) [-0.191; 0.079] [-0.119; 0.011]
Repeated p-value (1) 0.1150 0.0086
Repeated p-value (2) 0.2429 0.0274

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Performing the same comparisons as in stage \(1\), one can see: The global null is to be rejected (\(3.014 > 2.511\)). Subsequently, the hypothesis for the first active treatment is rejected, since \(3.182 > 2.511\) indicating that the first active arm performs better than control. The same result can be obtained by recognizing that the repeated p-value (1) of \(0.0086\) falls below \(0.025\). The consequence is that this arm can be discontinued early due to efficacy. However, since the second treatment arm is not tested significant (\(2.464 < 2.511\)) and early stopping for efficacy is true only when all active treatments appear to be significant, study will continue up to the the final stage with the second treatment arm only. Again, no futility stop occurs. It should be noted here that the adjusted stage-wise p-values cannot directly be used for testing, but the values do only base on the second stage data. Since an inverse normal combination test is performed with weights given by \(\frac{1}{3}\) here, the first and second stage p-values can be used to calculate the overall adjusted test statistics, exemplarily \(\frac{\sqrt{\frac{1}{3}}*\Phi^{-1}(1-0.0063)+\sqrt{\frac{1}{3}}*\Phi^{-1}(1-0.0384)}{\sqrt{\frac{2}{3}}} \approx 3.014\).

Third-stage-dataset:

genData_3 <- getDataset(
    events1      = c(4, 7, NA),
    events2      = c(8, 7, 6),
    events3      = c(16, 15, 16),
    sampleSizes1 = c(153, 155, NA),
    sampleSizes2 = c(157, 155, 156),
    sampleSizes3 = c(156, 155, 160)
)
genData_3 |> summary()

Dataset of multi-arm rates

The dataset contains the sample sizes and events of two treatment groups and one control group. The total number of looks is three; stage-wise and cumulative data are included.

Stage 1 1 1 2 2 2 3 3 3
Group 1 2 3 1 2 3 1 2 3
Stage-wise sample size 153 157 156 155 155 155 NA 156 160
Cumulative sample size 153 157 156 308 312 311 NA 468 471
Stage-wise number of events 4 8 16 7 7 15 NA 6 16
Cumulative number of events 4 8 16 11 15 31 NA 21 47

Final analysis:

results_3 <- getAnalysisResults(
    design = d_IN,
    dataInput = genData_3,
    directionUpper = FALSE,
    intersectionTest = "Simes"
)
results_3 |> summary()

Multi-arm analysis results for a binary endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm test for rates, Simes intersection test, normal approximation test. H0: pi(i) - pi(control) = 0 against H1: pi(i) - pi(control) < 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) -0.076 -0.064
Cumulative effect size (2) -0.052 -0.052 -0.055
Cumulative treatment rate (1) 0.026 0.036
Cumulative treatment rate (2) 0.051 0.048 0.045
Cumulative control rate 0.103 0.100 0.100
Stage-wise test statistic (1) -2.730 -1.770
Stage-wise test statistic (2) -1.716 -1.770 -2.149
Stage-wise p-value (1) 0.0032 0.0384
Stage-wise p-value (2) 0.0431 0.0384 0.0158
Adjusted stage-wise p-value (1, 2) 0.0063 0.0384 0.0158
Adjusted stage-wise p-value (1) 0.0032 0.0384
Adjusted stage-wise p-value (2) 0.0431 0.0384 0.0158
Overall adjusted test statistic (1, 2) 2.493 3.014 3.702
Overall adjusted test statistic (1) 2.730 3.182
Overall adjusted test statistic (2) 1.716 2.464 3.253
Test action: reject (1) FALSE TRUE TRUE
Test action: reject (2) FALSE FALSE TRUE
Conditional rejection probability (1) 0.2907 0.7911
Conditional rejection probability (2) 0.1204 0.5133
95% repeated confidence interval (1) [-0.212; 0.043] [-0.130; -0.005]
95% repeated confidence interval (2) [-0.191; 0.079] [-0.119; 0.011] [-0.099; -0.013]
Repeated p-value (1) 0.1150 0.0086
Repeated p-value (2) 0.2429 0.0274 0.0006

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Considering either e.g. overall adjusted test statistics for intersection and single hypothesis or repeated p-values, or directly referring to Test action: reject (2), one can conclude that the study claimed success since the first active treatment arm has already been tested significantly in the second stage while the second active treatment arm appears to be superior to control in the final stage.

Visualization of the analyses can be done graphically by illustrating the repeated confidence intervals, while one can see how the intervals keep narrowing along the stages because of increasing cumulative sample sizes and consistent trend observed across stages:

results_3 |> plot(type = 2)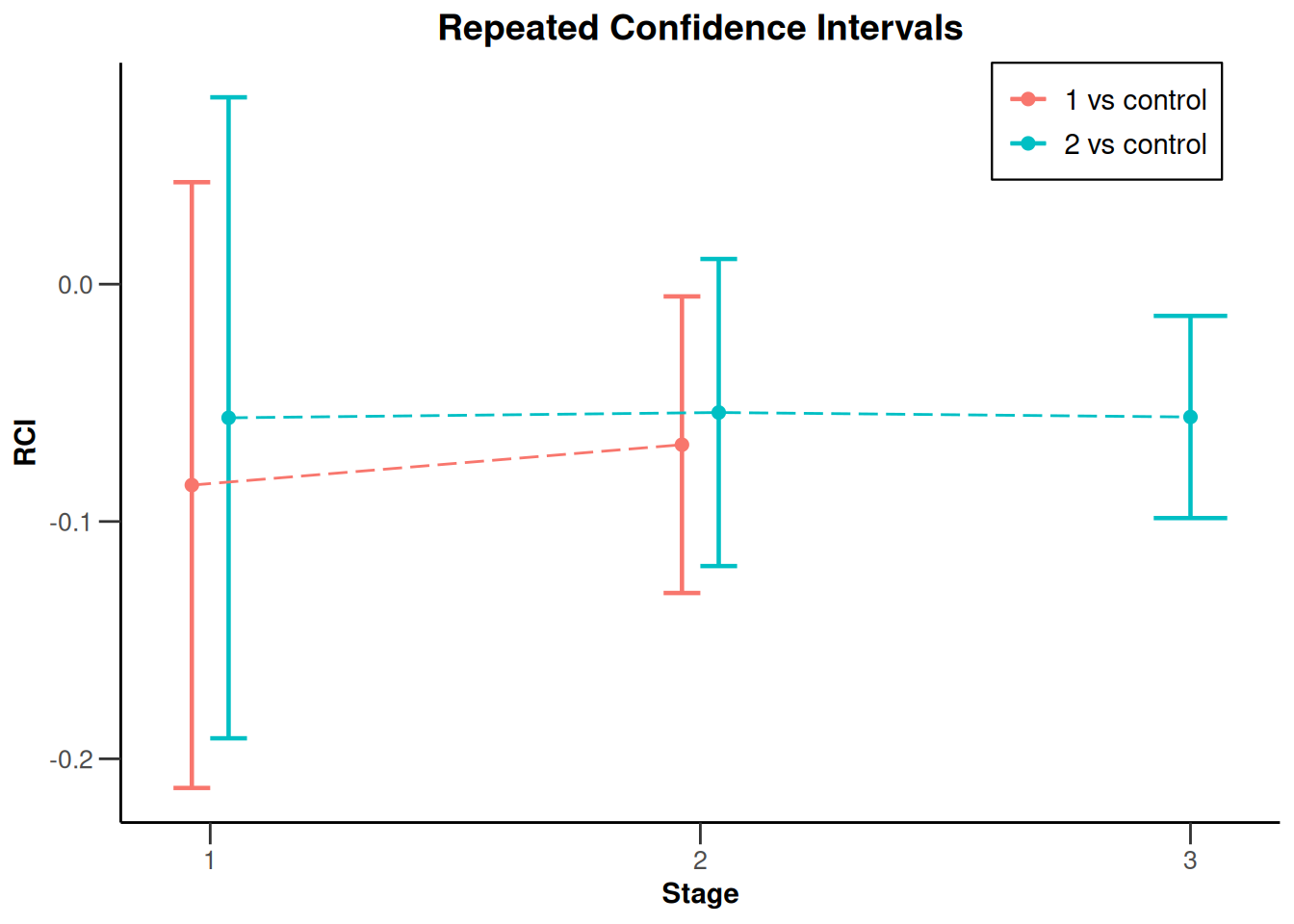

Second theoretical path

Assume that the first stage dataset does not differ from the first generic example (thus, nor the analysis results), then a second stage dataset could be:

genData_4 <- getDataset(
    events1      = c(4, 9),
    events2      = c(8, 23),
    events3      = c(16, 15),
    sampleSizes1 = c(153, 155),
    sampleSizes2 = c(157, 155),
    sampleSizes3 = c(156, 155)
)

Note the high event number in the second active treatment arm.

Analysis results:

results_4 <- getAnalysisResults(
    design = d_IN,
    dataInput = genData_4,
    directionUpper = FALSE,
    intersectionTest = "Simes"
)
results_4 |> summary()

Multi-arm analysis results for a binary endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm test for rates, Simes intersection test, normal approximation test. H0: pi(i) - pi(control) = 0 against H1: pi(i) - pi(control) < 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) -0.076 -0.057
Cumulative effect size (2) -0.052 0.000
Cumulative treatment rate (1) 0.026 0.042
Cumulative treatment rate (2) 0.051 0.099
Cumulative control rate 0.103 0.100
Stage-wise test statistic (1) -2.730 -1.275
Stage-wise test statistic (2) -1.716 1.385
Stage-wise p-value (1) 0.0032 0.1011
Stage-wise p-value (2) 0.0431 0.9170
Adjusted stage-wise p-value (1, 2) 0.0063 0.2023
Adjusted stage-wise p-value (1) 0.0032 0.1011
Adjusted stage-wise p-value (2) 0.0431 0.9170
Overall adjusted test statistic (1, 2) 2.493 2.352
Overall adjusted test statistic (1) 2.730 2.832
Overall adjusted test statistic (2) 1.716 0.234
Test action: reject (1) FALSE FALSE
Test action: reject (2) FALSE FALSE
Conditional rejection probability (1) 0.2907 0.4500
Conditional rejection probability (2) 0.1204 0.0009
95% repeated confidence interval (1) [-0.212; 0.043] [-0.125; 0.003]
95% repeated confidence interval (2) [-0.191; 0.079] [-0.080; 0.075]
Repeated p-value (1) 0.1150 0.0340
Repeated p-value (2) 0.2429 0.2429

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

As one can see, the global null hypothesis can not be rejected since \(2.352 < 2.511\). However, the second treatment arm results in a stop due to futility, since, after not rejecting the global null, \(0.234 < 0.414\) as indicated by the overall adjusted test statistic. That means this study course would lead to continuation only with active treatment arm \(1\).

Subsequent final stage dataset:

genData_5 <- getDataset(
    events1      = c(4, 9, 7),
    events2      = c(8, 23, NA),
    events3      = c(16, 15, 16),
    sampleSizes1 = c(153, 155, 165),
    sampleSizes2 = c(157, 155, NA),
    sampleSizes3 = c(156, 155, 160)
)
genData_5 |> summary()

Dataset of multi-arm rates

The dataset contains the sample sizes and events of two treatment groups and one control group. The total number of looks is three; stage-wise and cumulative data are included.

Stage 1 1 1 2 2 2 3 3 3
Group 1 2 3 1 2 3 1 2 3
Stage-wise sample size 153 157 156 155 155 155 165 NA 160
Cumulative sample size 153 157 156 308 312 311 473 NA 471
Stage-wise number of events 4 8 16 9 23 15 7 NA 16
Cumulative number of events 4 8 16 13 31 31 20 NA 47

Note that recruitment for treatment arm \(2\) has been terminated after stage \(2\).

Final stage analysis:

results_5 <- getAnalysisResults(
    design = d_IN,
    dataInput = genData_5,
    directionUpper = FALSE,
    intersectionTest = "Simes"
)
results_5 |> summary()

Multi-arm analysis results for a binary endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm test for rates, Simes intersection test, normal approximation test. H0: pi(i) - pi(control) = 0 against H1: pi(i) - pi(control) < 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) -0.076 -0.057 -0.058
Cumulative effect size (2) -0.052 0.000
Cumulative treatment rate (1) 0.026 0.042 0.042
Cumulative treatment rate (2) 0.051 0.099
Cumulative control rate 0.103 0.100 0.100
Stage-wise test statistic (1) -2.730 -1.275 -2.024
Stage-wise test statistic (2) -1.716 1.385
Stage-wise p-value (1) 0.0032 0.1011 0.0215
Stage-wise p-value (2) 0.0431 0.9170
Adjusted stage-wise p-value (1, 2) 0.0063 0.2023 0.0215
Adjusted stage-wise p-value (1) 0.0032 0.1011 0.0215
Adjusted stage-wise p-value (2) 0.0431 0.9170
Overall adjusted test statistic (1, 2) 2.493 2.352 3.089
Overall adjusted test statistic (1) 2.730 2.832 3.481
Overall adjusted test statistic (2) 1.716 0.234
Test action: reject (1) FALSE FALSE TRUE
Test action: reject (2) FALSE FALSE FALSE
Conditional rejection probability (1) 0.2907 0.4500
Conditional rejection probability (2) 0.1204 0.0009
95% repeated confidence interval (1) [-0.212; 0.043] [-0.125; 0.003] [-0.102; -0.017]
95% repeated confidence interval (2) [-0.191; 0.079] [-0.080; 0.075]
Repeated p-value (1) 0.1150 0.0340 0.0010
Repeated p-value (2) 0.2429 0.2429

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Since per definition, success of one treatment arm suffices to declare study success, that is the conclusion one comes to due to significance of treatment arm \(1\). Stopping treatment arm \(2\) earlier therefore did not influence the positive result.

Landmark analysis with Greenwood’s formula

A landmark analysis is an analysis where, given a predefined and fixed point in time, survival probabilities at that specific time point are to be compared between different groups, such as active treatment and control group.

As previously mentioned, rpact itself does not support the procedure of comparing survival probabilities (more precisely estimates) at a specific point in time with standard error being calculated by Greenwoods formula, but bases on simple rate comparisons only. However, a R package called gestate supports various survival analysis methods, including landmark analysis. Firstly, one needs to load the package:

library(gestate)

Then, since gestates’ functionality bases on curve subjects and the analysis approach bases on survival data, the distribution of the data from treatment and control groups need to be specified. Assume that the data in the control group follows an exponential distribution Exp(\(\lambda_c\))-distribution with \(\lambda_c=0.1\) and the treatment groups follow Exp(\(\lambda_{t1}\))- and Exp(\(\lambda_{t2}\))-distribution with \(\lambda_{t1}=\lambda_{t2}=0.1*0.5=0.05\) respectively (hazard ratio of \(0.5\), heuristically representing the assumed treatment effect of a \(50\%\) rate-reduction), while other options would be to assume Weibull or piecewise Exponential distribution. This is initialized using:

effect <- 0.5

# initializing assumed distributions of different treatment arms as well as control
dist_c <- Exponential(lambda = 0.1)
dist_t1 <- Exponential(lambda = 0.1 * (1 - effect))
dist_t2 <- Exponential(lambda = 0.1 * (1 - effect))

Then, another curve that needs to be initialized is the recruitment curve. Gestate covers the potential assumptions of e.g. having instantaneous, linear or piecewise linear recruitment. In many applications, assuming linear (e.g. constant rate) recruitment might be suitable, thus this is what might be used here as well. Note that the subject number equal the numbers that have been calculated in chapter \(2\) and, since measuring study duration in month is common, one may assume a total recruitment length of \(18 \, month = 1.5 \, years\). The data will later on be used to estimate survival probabilities and standard errors, subsequently to be used as input for the rpact continuous endpoint module. Since the mean, standard deviation and sample sizes in the dataset input all need to be stage-wise because of the use of inverse normal combination test, data simulation will also be done separately per stage per arm, resulting in a maximum of 9 simulated datasets in this application. Further, since the information levels are equally spread along the three stages, each stage-wise dataset will base on a recruitment of \(157\) subjects and a recruitment length of \(6 \, month\). Assuming an individual observation time of \(1 \, month\), one results in a total duration of \(7 \, month\) per stage:

# equally sized arms and stages
n <- 157

# maximum duration of each stage
maxtime <- 7

# initialize recruitment for control group
recruitment_c <- LinearR(Nactive = 0, Ncontrol = n, rlength = 6)

# initialize recruitment for treatment groups, here: equal
recruitment_t1 <- LinearR(Nactive = n, Ncontrol = 0, rlength = 6)
recruitment_t2 <- LinearR(Nactive = n, Ncontrol = 0, rlength = 6)

As already mentioned in chapter \(1\) (initialization of design), the interim analyses are to be performed at \(I_1 = \frac{1}{3}\) and \(I_2 = \frac{2}{3}\) with \(I\) denoting the information fraction and the index denoting the stage. Since information here stands in \(1:1\) correlation with sample size one can conclude that interims should be performed after \(6\) month and after \(12\) month of recruitment. Censoring could be specified through the variables active_dcurve, control_dcurve, however, in trials where no or only few censoring/dropout might be a reasonable assumption, these variables can be left on default (=Blank()). The only remaining type of censoring is censoring due to end of observation, e.g. subjects having had no event before study ends are considered censored.

Having made assumptions on data distribution, recruitment and censoring, simulating patient level survival data works as follows. It should be noted here that following simulations and data manipulations are demonstrated for the first stage data, however, second and third stage data is simulated and manipulated similarly.

# simulating data for all arms and stages independently (needed for dataset input)

# first stage, all arms, last index represents the stage
example_data_long_t1_1 <- simulate_trials(
    active_ecurve = dist_t1,
    control_ecurve = Blank(),
    rcurve = recruitment_t1,
    assess = maxtime,
    iterations = 1,
    seed = 1,
    detailed_output = TRUE
)

example_data_long_t2_1 <- simulate_trials(
    active_ecurve = dist_t2,
    control_ecurve = Blank(),
    rcurve = recruitment_t2,
    assess = maxtime,
    iterations = 1,
    seed = 2,
    detailed_output = TRUE
)

example_data_long_c_1 <- simulate_trials(
    active_ecurve = Blank(),
    control_ecurve = dist_c,
    rcurve = recruitment_c,
    assess = maxtime,
    iterations = 1,
    seed = 3,
    detailed_output = TRUE
)

kable(head(example_data_long_t1_1, 10))
Time Censored Trt Iter ETime CTime Rec_Time Assess Max_F RCTime
4.136118 1 2 1 15.103637 Inf 2.8638823 7 Inf 4.136118
2.375578 1 2 1 23.632856 Inf 4.6244223 7 Inf 2.375578
2.914134 0 2 1 2.914134 Inf 0.1667227 7 Inf 6.833277
2.795905 0 2 1 2.795905 Inf 3.1638647 7 Inf 3.836135
1.718086 1 2 1 8.721372 Inf 5.2819144 7 Inf 1.718086
4.761620 1 2 1 57.899371 Inf 2.2383802 7 Inf 4.761620
6.712245 1 2 1 24.591241 Inf 0.2877548 7 Inf 6.712245
6.168230 1 2 1 10.793657 Inf 0.8317695 7 Inf 6.168230
5.071047 1 2 1 19.131350 Inf 1.9289527 7 Inf 5.071047
2.940920 0 2 1 2.940920 Inf 0.9289897 7 Inf 6.071010

The table above provide information on patient level, such as time (to event), treatment group, time of event (if observed), assessment timing and recruitment time. To achieve that every subject only has an individual observation time of \(1 \, month\), one can manually set the censoring indicator to \(1\) whenever no event has happened or the simulation indicates that an event has happened only after the fixed observation time.

# Check: if time to event (first column) is >=1, subject is censored
example_data_long_t1_1[which(example_data_long_t1_1[, 1] > 1), 2] <- 1
example_data_long_t2_1[which(example_data_long_t2_1[, 1] > 1), 2] <- 1
example_data_long_c_1[which(example_data_long_c_1[, 1] > 1), 2] <- 1

After doing this, since the administrative censoring due to end of observation has manually been manipulated, the time of censoring in the last column can manually be corrected according to the changes:

# if censoring indicator==1, the censoring time is set to event time
# according to the previous changes

# stage 1
example_data_long_t1_1[which(example_data_long_t1_1[, 2] == 1), 9] <-
    example_data_long_t1_1[which(example_data_long_t1_1[, 2] == 1), 1]

example_data_long_t2_1[which(example_data_long_t2_1[, 2] == 1), 9] <-
    example_data_long_t2_1[which(example_data_long_t2_1[, 2] == 1), 1]

example_data_long_c_1[which(example_data_long_c_1[, 2] == 1), 9] <-
    example_data_long_c_1[which(example_data_long_c_1[, 2] == 1), 1]

Though working on subject level data (if available) is commonly recommended, one could be interested in tables containing time, number of subjects at risk, survival probabilities and respective standard errors, henceforth referred to as life tables. After setting the assessment time to the defined \(7 \, month\), for creating the life tables, the commands Surv() and survfit() from the R package survival are used:

# needs to be run in case package has not yet been installed
library(survival)

# setting desired assessment time
example_data_short_t1_1 <- set_assess_time(example_data_long_t1_1, maxtime)
example_data_short_t2_1 <- set_assess_time(example_data_long_t2_1, maxtime)
example_data_short_c_1 <- set_assess_time(example_data_long_c_1, maxtime)

# Creating live tables for each group depending on the stage
# at first landmark time point
lt_t1_1 <- summary(survfit(Surv(
    example_data_short_t1_1[, "Time"],
    1 - example_data_short_t1_1[, "Censored"]
) ~ 1, error = "greenwood"))
lt_t2_1 <- summary(survfit(Surv(
    example_data_short_t2_1[, "Time"],
    1 - example_data_short_t2_1[, "Censored"]
) ~ 1, error = "greenwood"))
lt_c_1 <- summary(survfit(Surv(
    example_data_short_c_1[, "Time"],
    1 - example_data_short_c_1[, "Censored"]
) ~ 1, error = "greenwood"))

kable(head(cbind(
    "Time" = lt_t1_1$time, "n.risk" = lt_t1_1$n.risk,
    "n.event" = lt_t1_1$n.event, "surv.prob." = lt_t1_1$surv,
    "Greenwoods SE" = lt_t1_1$std.err
), 10))
Time n.risk n.event surv.prob. Greenwoods SE
0.4050083 157 1 0.9936306 0.0063491
0.7430455 156 1 0.9872611 0.0089502
0.7453705 155 1 0.9808917 0.0109263
1.0411090 152 1 0.9744385 0.0126170
1.1852241 143 1 0.9676242 0.0142506
1.1887832 142 1 0.9608100 0.0156951
1.3882469 136 1 0.9537452 0.0170959
1.7934816 127 1 0.9462354 0.0185375
1.8221775 125 1 0.9386655 0.0198748
1.9769123 119 1 0.9307776 0.0212154

This table created above contains time, number of subjects at risk, number of events, survival probability estimation and standard error estimation, thus allowing for creating a Kaplan-Meier-Plot to visualize the development of survival probability in time. Note that choosing error="greenwood" leads to the desired SE estimation. One could also discretize the time into intervals to obtain life tables with consistent time steps, if desired. Exemplary Kaplan-Meier-Plots for the different treatment groups at the different stages are created below:

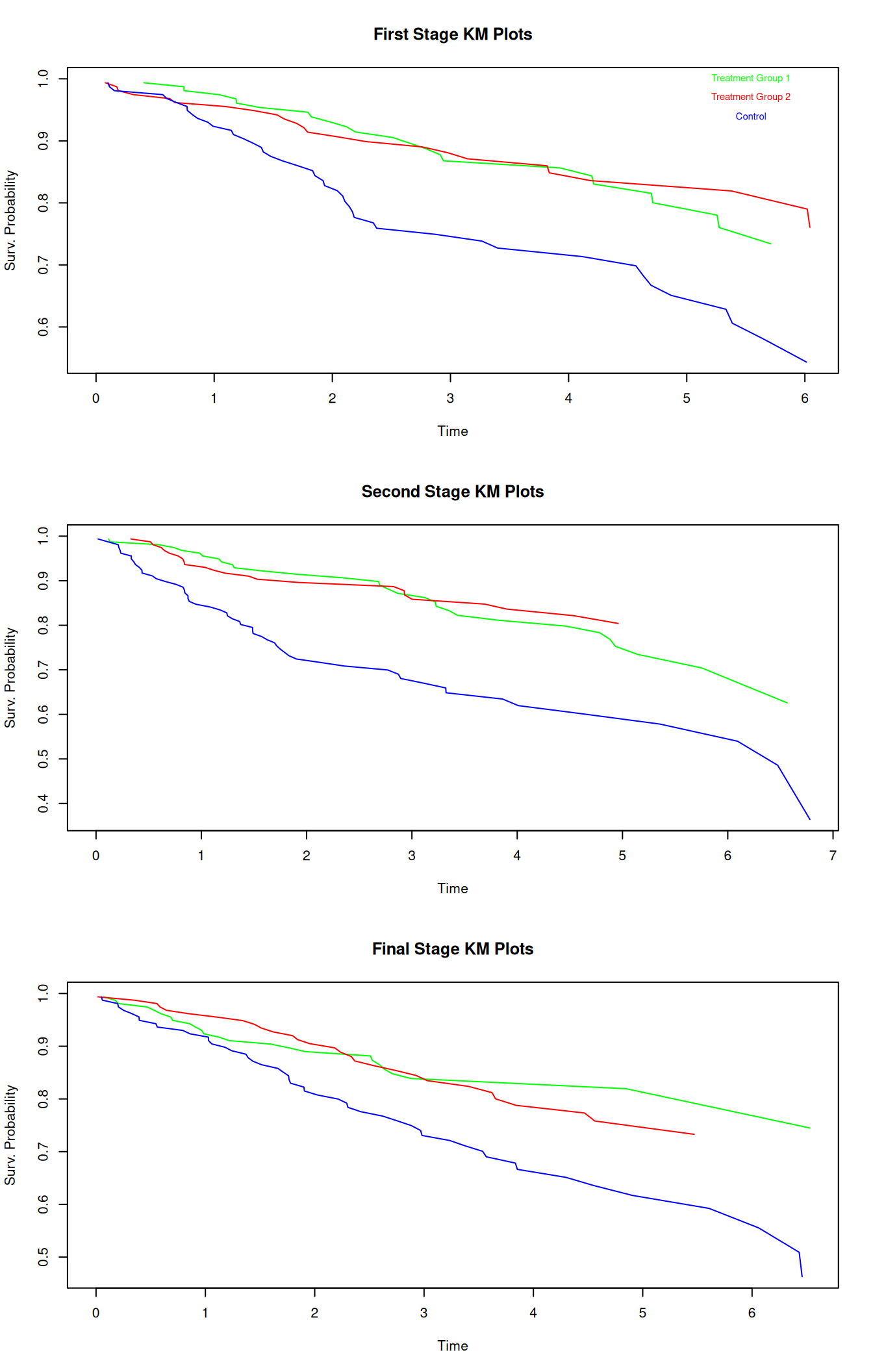
While the survival probabilities from the treatment arms develop rather similarly for the independently simulated stages, the figures demonstrate that, besides few early exceptions, the survival probabilities from the control group falls below the survival probabilities of the treatment groups almost constantly, indicating that the groups might actually (i.e. potentially statistically significant) differ.

As previously mentioned, the continuous module of rpact is now used to perform the landmark analysis of the gestate-simulated data. Note here that this is a valid approximation whenever assuming the survival probability estimates to be normally distributed is reasonable. To initialize continuous datasets, estimated survival probabilities from the life tables above will be used as mean, the transformed Greenwood SE estimations will be used as standard deviation and the sample size from the earlier sample size calculations is used, making the simplifying assumption of no dropouts. The first stage continuous dataset therefore is:

lm <- 7

# first stage dataset
dataset_1 <- getDataset(
    # accessing the survival probability values at the timepoint closest to the desired one
    means1 = c(lt_t1_1$surv[which(abs(lt_t1_1$time - lm) == min(abs(lt_t1_1$time - lm)))]),
    means2 = c(lt_t2_1$surv[which(abs(lt_t2_1$time - lm) == min(abs(lt_t2_1$time - lm)))]),
    means3 = c(lt_c_1$surv[which(abs(lt_c_1$time - lm) == min(abs(lt_c_1$time - lm)))]),
    stDevs1 = c(lt_t1_1$std.err[which(abs(lt_t1_1$time - lm) ==
        min(abs(lt_t1_1$time - lm)))] * sqrt(n)),
    stDevs2 = c(lt_t2_1$std.err[which(abs(lt_t2_1$time - lm) ==
        min(abs(lt_t2_1$time - lm)))] * sqrt(n)),
    stDevs3 = c(lt_c_1$std.err[which(abs(lt_c_1$time - lm) ==
        min(abs(lt_c_1$time - lm)))] * sqrt(n)),
    n1 = c(n),
    n2 = c(n),
    n3 = c(n)
)
dataset_1 |> summary()

Dataset of multi-arm means

The dataset contains the sample sizes, means, and standard deviations of two treatment groups and one control group.

Stage 1 1 1
Group 1 2 3
Sample size 157 157 157
Mean 0.734 0.761 0.543
Standard deviation 0.657 0.661 0.811

The explicit estimates can be seen using the summary()-command.

Note that the highest index (\(=3\)) represents the control group. Since the time in the life table data has not been structured into intervals of equal length, the datasets do mostly not have survival probabilities and standard error entries exactly at the given landmark time point, which is why the closest point in time is chosen here. Analysis of the data according to the group sequential design in this vignette can then be done by:

result_1 <- getAnalysisResults(
    dataInput = dataset_1, design = d_IN,
    intersectionTest = "Simes",
    normalApproximation = TRUE, varianceOption = "pairwisePooled"
)
result_1 |> summary()

Multi-arm analysis results for a continuous endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm t-test, Simes intersection test, normal approximation test, pairwise pooled variances option. H0: mu(i) - mu(control) = 0 against H1: mu(i) - mu(control) > 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) 0.191
Cumulative effect size (2) 0.217
Cumulative (pooled) standard deviation 0.714
Stage-wise test statistic (1) 2.287
Stage-wise test statistic (2) 2.601
Stage-wise p-value (1) 0.0111
Stage-wise p-value (2) 0.0046
Adjusted stage-wise p-value (1, 2) 0.0093
Adjusted stage-wise p-value (1) 0.0111
Adjusted stage-wise p-value (2) 0.0046
Overall adjusted test statistic (1, 2) 2.354
Overall adjusted test statistic (1) 2.287
Overall adjusted test statistic (2) 2.601
Test action: reject (1) FALSE
Test action: reject (2) FALSE
Conditional rejection probability (1) 0.2359
Conditional rejection probability (2) 0.2530
95% repeated confidence interval (1) [-0.133; 0.514]
95% repeated confidence interval (2) [-0.107; 0.542]
Repeated p-value (1) 0.1425
Repeated p-value (2) 0.1331

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Since the overall adjusted test statistic for the intersection hypotheses (\(=2.354\)) does not exceed the first stage critical value of \(3.710\), the intersection hypothesis of having no effect in either one of the treatment groups cannot be rejected, while e.g. repeated p-values lead to the same results. Furthermore, since all of the applicable test statistics do not fall below the futility bound of \(0.149\), the study ordinarily proceeds to the second stage:

dataset_2 <- getDataset(
    means1 = c(
        lt_t1_1$surv[which(abs(lt_t1_1$time - lm) == min(abs(lt_t1_1$time - lm)))],
        lt_t1_2$surv[which(abs(lt_t1_2$time - lm) == min(abs(lt_t1_2$time - lm)))]
    ),
    means2 = c(
        lt_t2_1$surv[which(abs(lt_t2_1$time - lm) == min(abs(lt_t2_1$time - lm)))],
        lt_t2_2$surv[which(abs(lt_t2_2$time - lm) == min(abs(lt_t2_2$time - lm)))]
    ),
    means3 = c(
        lt_c_1$surv[which(abs(lt_c_1$time - lm) == min(abs(lt_c_1$time - lm)))],
        lt_c_2$surv[which(abs(lt_c_2$time - lm) == min(abs(lt_c_2$time - lm)))]
    ),
    stDevs1 = c(
        lt_t1_1$std.err[which(abs(lt_t1_1$time - lm) ==
            min(abs(lt_t1_1$time - lm)))] * sqrt(n),
        lt_t1_2$std.err[
            which(abs(lt_t1_2$time - lm) == min(abs(lt_t1_2$time - lm)))
        ] * sqrt(n)
    ),
    stDevs2 = c(
        lt_t2_1$std.err[which(abs(lt_t2_1$time - lm) ==
            min(abs(lt_t2_1$time - lm)))] * sqrt(n),
        lt_t2_2$std.err[which(abs(lt_t2_2$time - lm) ==
            min(abs(lt_t2_2$time - lm)))] * sqrt(n)
    ),
    stDevs3 = c(
        lt_c_1$std.err[which(abs(lt_c_1$time - lm) == min(abs(lt_c_1$time - lm)))]
        * sqrt(n),
        lt_c_2$std.err[which(abs(lt_c_2$time - lm) == min(abs(lt_c_2$time - lm)))]
        * sqrt(n)
    ),
    n1 = c(n, n),
    n2 = c(n, n),
    n3 = c(n, n)
)

result_2 <- getAnalysisResults(
    dataInput = dataset_2, design = d_IN,
    intersectionTest = "Simes", normalApproximation = TRUE,
    varianceOption = "pairwisePooled"
)
result_2 |> summary()

Multi-arm analysis results for a continuous endpoint (2 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm t-test, Simes intersection test, normal approximation test, pairwise pooled variances option. H0: mu(i) - mu(control) = 0 against H1: mu(i) - mu(control) > 0.

Stage 1 2 3
Fixed weight 0.577 0.577 0.577
Cumulative alpha spent 0.0001 0.0060 0.0250
Stage levels (one-sided) 0.0001 0.0060 0.0231
Efficacy boundary (z-value scale) 3.710 2.511 1.993
Futility boundary (z-value scale) 0.149 0.414
Cumulative effect size (1) 0.191 0.226
Cumulative effect size (2) 0.217 0.329
Cumulative (pooled) standard deviation 0.714 0.931
Stage-wise test statistic (1) 2.287 1.769
Stage-wise test statistic (2) 2.601 3.512
Stage-wise p-value (1) 0.0111 0.0384
Stage-wise p-value (2) 0.0046 0.0002
Adjusted stage-wise p-value (1, 2) 0.0093 0.0004
Adjusted stage-wise p-value (1) 0.0111 0.0384
Adjusted stage-wise p-value (2) 0.0046 0.0002
Overall adjusted test statistic (1, 2) 2.354 4.015
Overall adjusted test statistic (1) 2.287 2.868
Overall adjusted test statistic (2) 2.601 4.323
Test action: reject (1) FALSE TRUE
Test action: reject (2) FALSE TRUE
Conditional rejection probability (1) 0.2359 0.7272
Conditional rejection probability (2) 0.2530 0.9870
95% repeated confidence interval (1) [-0.133; 0.514] [-0.005; 0.441]
95% repeated confidence interval (2) [-0.107; 0.542] [0.096; 0.527]
Repeated p-value (1) 0.1425 0.0119
Repeated p-value (2) 0.1331 0.0007

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Again referring to the overall adjusted test statistics, since \(4.015 > 2.511\), the global intersection hypothesis can be rejected in the second stage. Subsequently, the hypothesis of no effect in the first treatment group can be rejected because \(2.868 > 2.511\) and the hypothesis of no effect in the second treatment group can be rejected due to \(4.323\) exceeding the applicable critical value. Another testing approach would be to compare repeated p-values listed at the end of the output (\(0.0119, \, 0.0007\)) to the full significance level \(\alpha=0.025\).

As mentioned in the context of the simulations in chapter 5, study success can only be concluded when both treatment arms have been tested significantly against control. As this appears to be the case here, the study would have successfully finished at the second stage.

Closing remarks

This vignette demonstrated how to implement a MAMS study design given the case the futility bounds are only known on treatment effect scale, to perform simulations with special regards to treatment selection as well as how to analyze generic data using the binary module or perform landmark analysis with the support of gestate. Especially considering the final chapter about the landmark analysis, further investigations on how the results and characteristics such as \(\alpha\)-level control and/or the power behave could be done in subsequent research.

System: rpact 4.1.1, R version 4.4.2 (2024-10-31 ucrt), platform: x86_64-w64-mingw32

To cite R in publications use:

R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.

To cite package ‘rpact’ in publications use:

Wassmer G, Pahlke F (2024). rpact: Confirmatory Adaptive Clinical Trial Design and Analysis. R package version 4.1.1, https://www.rpact.com, https://github.com/rpact-com/rpact, https://rpact-com.github.io/rpact/, https://www.rpact.org.