Analysis of a Multi-Arm Design with a Binary Endpoint using rpact

Analysis
Rates
Multi-arm
This document shows how to analyse and interpret multi-arm designs for testing proportions with rpact.
Author

Gernot Wassmer Friedrich Pahlke

Published

February 16, 2024

Introduction

This vignette provides examples of how to analyse a trial with multiple arms and a binary endpoint. It shows how to calculate the conditional power at a given stage and to select/deselect treatment arms. For designs with multiple arms, rpact enables the analysis using the closed combination testing principle. For a description of the methodology please refer to Part III of the book “Group Sequential and Confirmatory Adaptive Designs in Clinical Trials” (Wassmer and Brannath, 2016).

Suppose the trial was conducted as a multi-arm multi-stage trial with three active treatments arms and a control arm when the trial started. In the interim stages, it should be possible to de-select treatment arms if the treatment effect is too small to show significance - assuming reasonable sample size - at the end of the trial. This should hold true even if a certain sample size increase was taken into account. The endpoint is a failure and it is intended to test each active arm against control. This is to test the hypotheses \[ H_{0i}:\pi_{\text{arm}i} = \pi_\text{control} \qquad\text{against} \qquad H_{1i}:\pi_{\text{arm}i} < \pi_\text{control}\;, \;i = 1,2,3\,,\] in the many-to-one comparisons setting. That is, it is intended to show that the failure rate is smaller in active arms as compared to control and so the power is directed towards negative values of \(\pi_{\text{arm}i} - \pi_\text{control}\).

Create the design

First, load the rpact package

library(rpact)
packageVersion("rpact") # version should be version 3.0 or later
[1] '4.0.0'

In rpact, we first have to select the combination test with the corresponding stopping boundaries to be used in the closed testing procedure. We choose a design with critical values within the Wang & Tsiatis \(\Delta\)-class of boundaries with \(\Delta = 0.25\). Planning two interim stages and a final stage, assuming equally sized stages, the design is defined through

designIN <- getDesignInverseNormal(
    kMax = 3, alpha = 0.025,
    typeOfDesign = "WT", deltaWT = 0.25
)
kable(summary(designIN))
Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA NA NA
WT 3 1 0.3333333 0.025 0.2 FALSE 0.25 1 0 0.0030614 2.741137 0.0030614
WT 3 2 0.6666667 0.025 0.2 FALSE 0.25 1 0 0.0123724 2.305012 0.0105830
WT 3 3 1.0000000 0.025 0.2 FALSE 0.25 1 0 0.0250000 2.082813 0.0186341

This definition fixes the weights in the combination test which are the same over the three stages. This is a reasonable choice although the amount of information seems to be not the same over the stages (see Wassmer, 2010).

Analysis

First stage

In each treatment and the control arm, subjects were randomized such that around 40 subjects per arm will be observed. Assume that the following actual sample sizes and failures in the control and the three experimental treatment arms were obtained for the first stage of the trial:

Arm n Failures
Active 1 42 7
Active 2 39 8
Active 3 38 14
Control 41 18

These data are defined as an rpact dataset with the function getDataset() for the later use in getAnalysisResults() through

dataRates <- getDataset(
    events1      =  7,
    events2      =  8,
    events3      = 14,
    events4      = 18,
    sampleSizes1 = 42,
    sampleSizes2 = 39,
    sampleSizes3 = 38,
    sampleSizes4 = 41
)

That is, you can use the getDataset() function in the usual way and simply extend it to the multiple treatment arms situation. Note that the arm with the highest index always refers to the control group. For the control group, specifically, it is mandatory to enter values over all stages. As we will see below, it is possible to omit information of de-selected active arms.

Using

results <- getAnalysisResults(
    design = designIN, dataInput = dataRates,
    directionUpper = FALSE
)
kable(summary(results))

one obtains the test results for the first stage of this trial (note the directionUpper = FALSE specification that yields small \(p\)-values for negative test statistics):

Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA
1 FALSE TRUE Dunnett 0.1666667 0.4390244 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE TRUE Dunnett 0.1666667 0.4390244 NA NA NA NA NA
1 FALSE TRUE Dunnett 0.1666667 0.4390244 NA NA NA NA NA
2 FALSE TRUE Dunnett 0.2051282 0.4390244 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE TRUE Dunnett 0.2051282 0.4390244 NA NA NA NA NA
2 FALSE TRUE Dunnett 0.2051282 0.4390244 NA NA NA NA NA
3 FALSE TRUE Dunnett 0.3684211 0.4390244 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE TRUE Dunnett 0.3684211 0.4390244 NA NA NA NA NA
3 FALSE TRUE Dunnett 0.3684211 0.4390244 NA NA NA NA NA

First of all, at the first interim no hypothesis can be rejected with the closed combination test. This is seen from the test action: reject (i) variable. It is remarkable, however, that the \(p\)-value for the comparison of treatment arm 1 against control (p = 0.0034) is quite small and even the \(p\)-value for the global intersection is (p(1, 2, 3) = 0.0095) is not too far from showing significance. It is important to know that, by default, the Dunnett many-to-one comparison test for binary data is used as the test for the intersection hypotheses, and the approximate pairwise score test (which is the signed square root of the \(\chi^2\) test) is used for the calculation of the separate \(p\)-values. Note that in this presentation the intersection tests for the whole closed system of hypotheses is provided such that the closed test can completely be reproduced.

The repeated \(p\)-values (0.0519, 0.0948, and 0.4568, respectively) precisely correspond with the test decision meaning that a repeated \(p\)-value is smaller or equal to the overall significance level (0.025) if and only if the corresponding hypothesis can be rejected at the considered stage. This direct correspondence is not generally true for the repeated confidence intervals (i.e., they can contain the value zero although the null hypothesis can be rejected), but it is true for the situation at hand. The repeated confidence intervals can be displayed with the plot(, type = 2) command by

plot(results, type = 2)

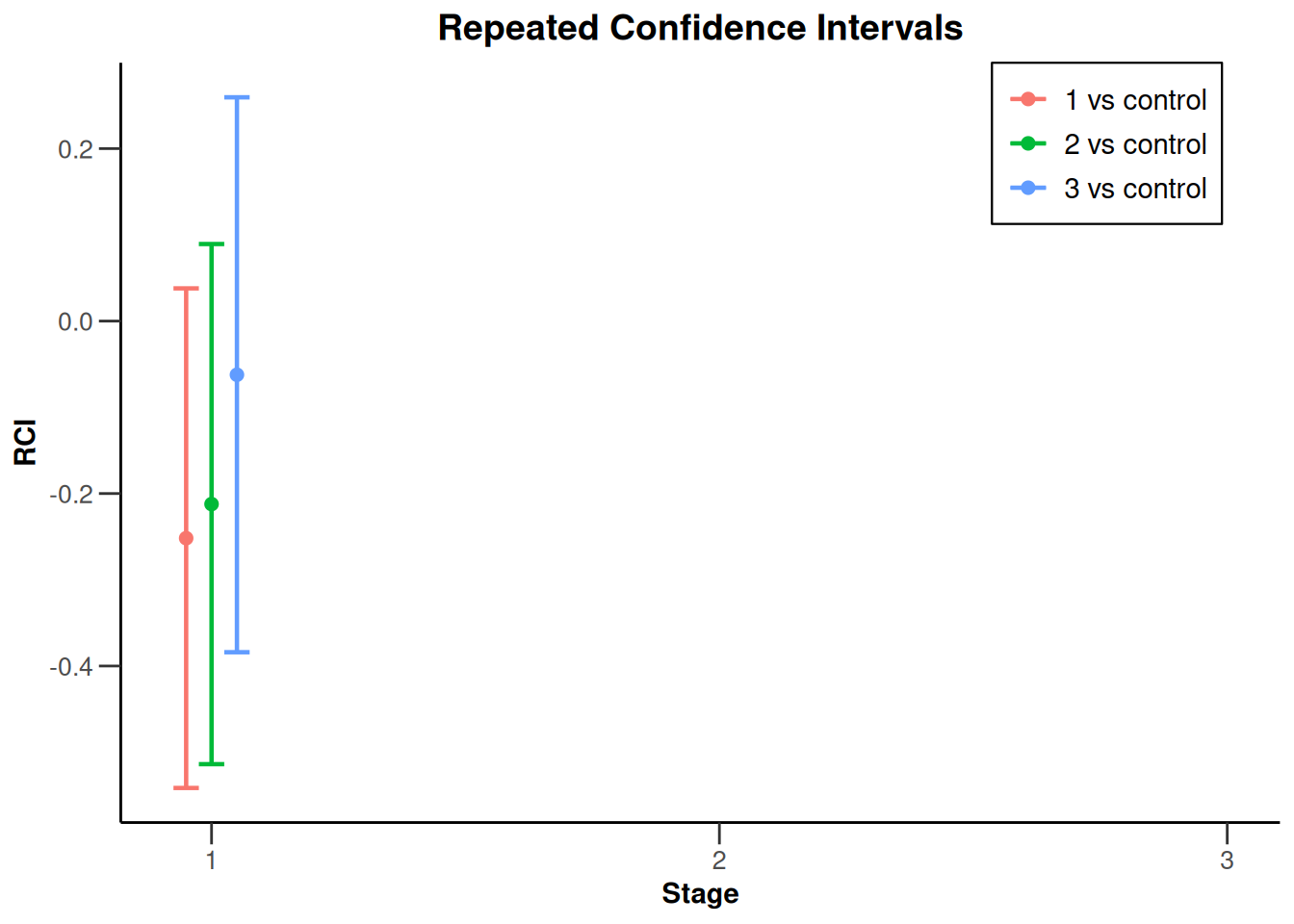
For assessing the conditional power, a sample size specification for the remaining stages needs to be done. We assume that around 80 subjects will be obtained per considered comparison (i.e., for both treatment arms together) and per stage. Use ?getAnalysisResults() to obtain the information about how to specify the parameter nPlanned. Assuming 80 subjects you have to re-run (options("rpact.summary.output.size" = "small") reduces the output of the summary)

options("rpact.summary.output.size" = "small")
results <- getAnalysisResults(
    design = designIN, dataInput = dataRates,
    directionUpper = FALSE, nPlanned = c(80, 80)
)
kable(summary(results))

to obtain

Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA NA
1 FALSE NA TRUE Dunnett 0.1666667 0.4390244 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE NA TRUE Dunnett 0.1666667 0.4390244 NA 0.9671737 NA NA NA
1 FALSE NA TRUE Dunnett 0.1666667 0.4390244 NA 0.9990060 NA NA NA
2 FALSE 80 TRUE Dunnett 0.2051282 0.4390244 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE 80 TRUE Dunnett 0.2051282 0.4390244 NA 0.8437870 NA NA NA
2 FALSE 80 TRUE Dunnett 0.2051282 0.4390244 NA 0.9846324 NA NA NA
3 FALSE 80 TRUE Dunnett 0.3684211 0.4390244 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE 80 TRUE Dunnett 0.3684211 0.4390244 NA 0.0238724 NA NA NA
3 FALSE 80 TRUE Dunnett 0.3684211 0.4390244 NA 0.1229080 NA NA NA

The Conditional power (i) variable shows very high power (esp. for the final stage) for treatment arms 1 and 2, but not for arm 3. Note that the conditional power is calculated under the assumption that the observed rates are the true rates. This can be changed, however, by setting piControl and/or piTreatments equal to the desired values (piTreatments can even be a vector), e.g.,

results <- getAnalysisResults(
    design = designIN, dataInput = dataRates,
    directionUpper = FALSE, nPlanned = c(80, 80),
    piTreatments = c(0.17, 0.2, 0.37),
    piControl = 0.44
)
kable(summary(results))
Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA NA
1 FALSE NA 0.17 0.44 TRUE Dunnett 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE NA 0.17 0.44 TRUE Dunnett NA 0.9647708 NA NA NA
1 FALSE NA 0.17 0.44 TRUE Dunnett NA 0.9988472 NA NA NA
2 FALSE 80 0.20 0.44 TRUE Dunnett 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE 80 0.20 0.44 TRUE Dunnett NA 0.8594191 NA NA NA
2 FALSE 80 0.20 0.44 TRUE Dunnett NA 0.9879184 NA NA NA
3 FALSE 80 0.37 0.44 TRUE Dunnett 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE 80 0.37 0.44 TRUE Dunnett NA 0.0235481 NA NA NA
3 FALSE 80 0.37 0.44 TRUE Dunnett NA 0.1212694 NA NA NA

Note that the title of the summary describes the situation under which the conditional power calculation is performed.

plot(results, type = 1, piTreatmentRange = c(0, 0.5), legendPosition = 3)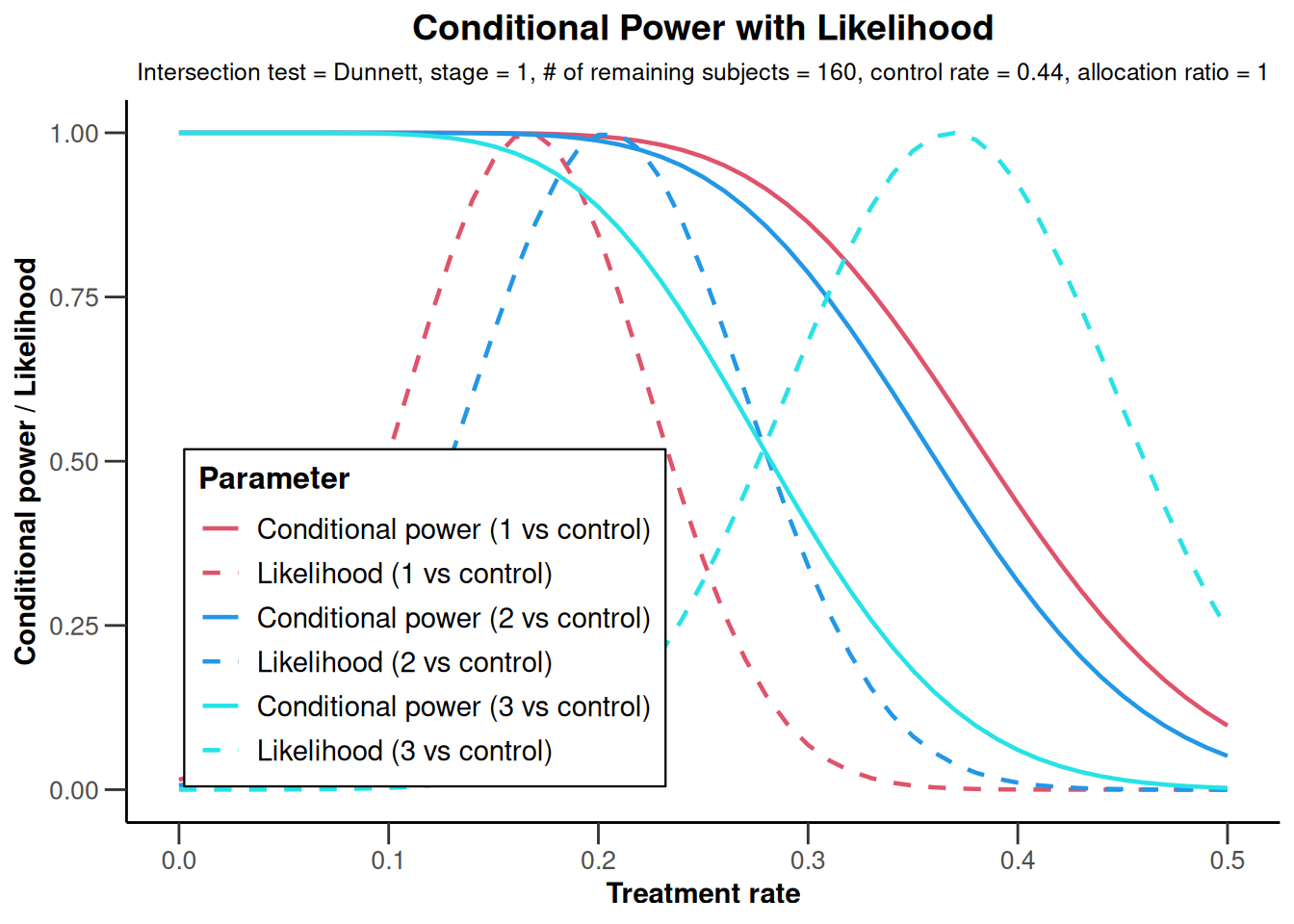

Altogether, based on the results of the first interim the decision to drop treatment arm 3 and to recruit further 40 patients to each treatment arms 1 and 2 (and to the control group) was taken.

Second stage

Also for the second stage, in each of the reaming treatment arms and the control arm, subjects were randomized such that around 40 subjects per arm will be observed. Assume the following failures and actual sample sizes in the control and the two remaining arms:

Arm n Failures
Active 1 37 9
Active 2 41 13
Active 3
Control 42 19

With getDataset(), these data for the second stage are appended to the first stage data as follows:

dataRates <- getDataset(
    events1 = c(7, 9),
    events2 = c(8, 13),
    events3 = c(14, NA),
    events4 = c(18, 19),
    sampleSizes1 = c(42, 37),
    sampleSizes2 = c(39, 41),
    sampleSizes3 = c(38, NA),
    sampleSizes4 = c(41, 42)
)

and the stage 2 results are obtained with

Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA
1 FALSE TRUE Dunnett 0.2025316 0.4457831 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE TRUE Dunnett 0.2025316 0.4457831 0.6571987 NA -0.4292516 -0.0370500 0.0065470
1 FALSE TRUE Dunnett 0.2025316 0.4457831 NA NA NA NA NA
2 FALSE TRUE Dunnett 0.2625000 0.4457831 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE TRUE Dunnett 0.2625000 0.4457831 0.3588963 NA -0.3802891 0.0239505 0.0255661
2 FALSE TRUE Dunnett 0.2625000 0.4457831 NA NA NA NA NA
3 FALSE TRUE Dunnett NA 0.4457831 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE TRUE Dunnett NA 0.4457831 NA NA NA NA NA
3 FALSE TRUE Dunnett NA 0.4457831 NA NA NA NA NA

Treatment arm 1 is significantly better than control, see Test action: reject (1), and reflected in both Repeated $p$-value (1) and the Repeated confidence interval (1) excluding 0. For treatment arm 2, however, significance could not be shown, although both, the global intersection hypothesis and the single hypothesis referring to treatment arm 2, can be rejected with the corresponding combination test. The reason for non-significance is the overall adjusted test statistic for testing \(H_{02}\cap H_{03}\) which is 2.295 < 2.305.

In order to show significance also for treatment arm 2, one might calculate the power if the sample size was reduced to 20 subjects per considered arm (treatment arm 2 and control). This is achieved through

Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA NA
1 FALSE NA TRUE Dunnett 0.2025316 0.4457831 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE NA TRUE Dunnett 0.2025316 0.4457831 0.6571987 NA -0.4292516 -0.0370500 0.0065470
1 FALSE NA TRUE Dunnett 0.2025316 0.4457831 NA 0.9830449 NA NA NA
2 FALSE NA TRUE Dunnett 0.2625000 0.4457831 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE NA TRUE Dunnett 0.2625000 0.4457831 0.3588963 NA -0.3802891 0.0239505 0.0255661
2 FALSE NA TRUE Dunnett 0.2625000 0.4457831 NA 0.8069037 NA NA NA
3 FALSE 40 TRUE Dunnett NA 0.4457831 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE 40 TRUE Dunnett NA 0.4457831 NA NA NA NA NA
3 FALSE 40 TRUE Dunnett NA 0.4457831 NA NA NA NA NA

showing that conditional power might be reduced to around 80% if the sample size was decreased. However, as showing in this graph

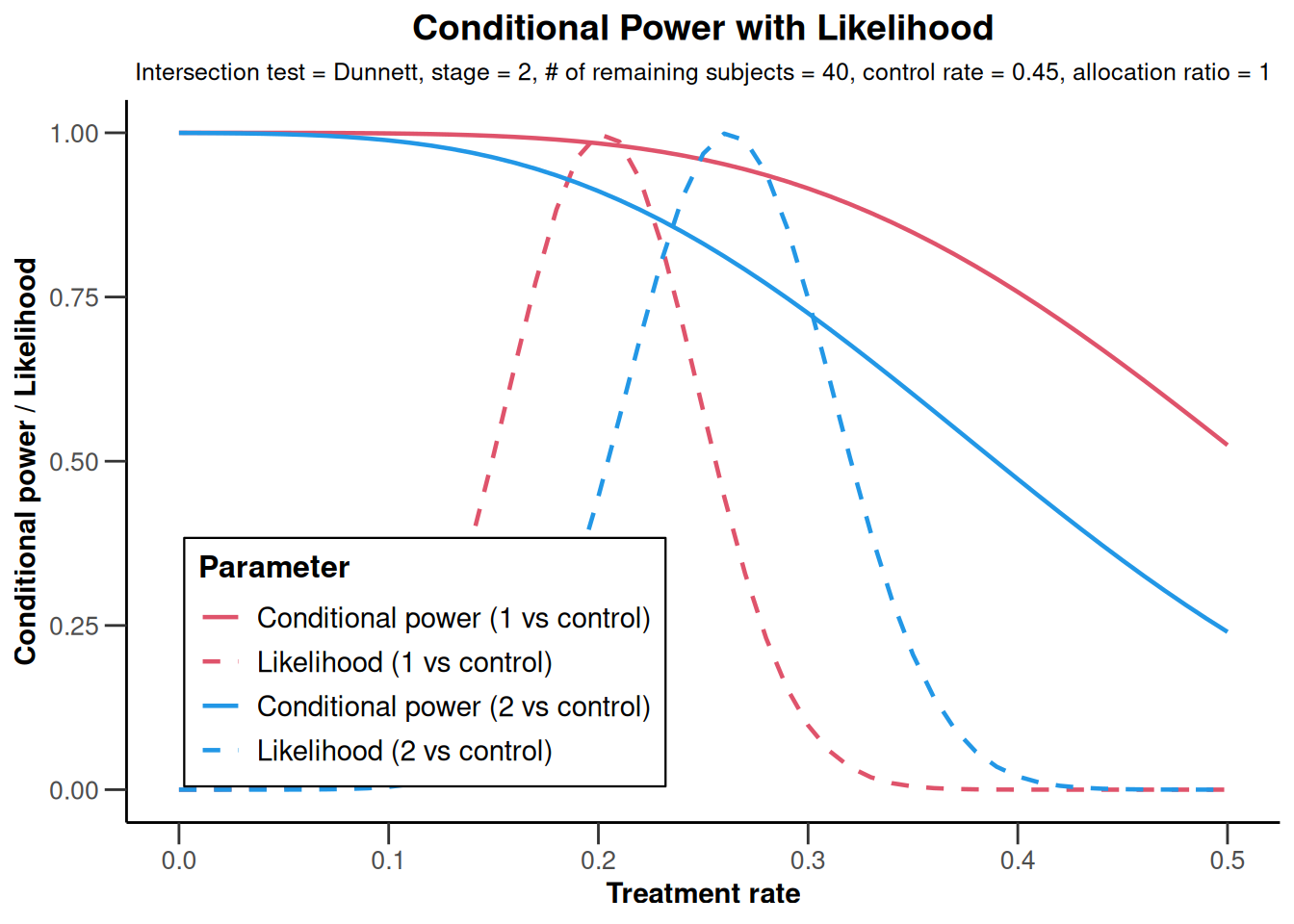
this is predominantly due to the relatively large observed overall failure rate in stage 2. Assuming a failure rate of (say) 20% yields conditional power of 91.1% which is obtained from

results <- getAnalysisResults(
    design = designIN, dataInput = dataRates,
    directionUpper = FALSE, nPlanned = 40,
    piTreatments = 0.2
)
kable(round(100 * results$conditionalPower[2, 3], 1))

Therefore, it might be reasonable to drop treatment arm 1 (for which significance was already shown) and compare treatment arm 2 only against control in the final stage.

Final stage

Assume the following sample sizes and failures for the final stage where only (additional) active arm 2 and control data were obtained.

Arm n Failures
Active 1
Active 2 18 7
Active 3
Control 19 11

These data for the final stage are entered as follows:

dataRates <- getDataset(
    events1 = c(7, 9, NA),
    events2 = c(8, 13, 7),
    events3 = c(14, NA, NA),
    events4 = c(18, 19, 11),
    sampleSizes1 = c(42, 37, NA),
    sampleSizes2 = c(39, 41, 18),
    sampleSizes3 = c(38, NA, NA),
    sampleSizes4 = c(41, 42, 19)
)

and

results <- getAnalysisResults(
    design = designIN, dataInput = dataRates,
    directionUpper = FALSE
)
kable(summary(results))

provides the results (significance for treatment arm 2 could additionally be shown):

Warning in is.na(parameterValues): is.na() auf Nicht-(Liste oder Vektor) des
Typs 'environment' angewendet
object NA NA NA NA NA NA NA NA NA NA
1 FALSE TRUE Dunnett NA 0.4705882 0.2646612 NA -0.5414861 0.0379012 0.0519075
1 FALSE TRUE Dunnett NA 0.4705882 0.6571987 NA -0.4292516 -0.0370500 0.0065470
1 FALSE TRUE Dunnett NA 0.4705882 NA NA NA NA NA
2 FALSE TRUE Dunnett 0.2857143 0.4705882 0.1708350 NA -0.5138410 0.0893263 0.0947951
2 FALSE TRUE Dunnett 0.2857143 0.4705882 0.3588963 NA -0.3802891 0.0239505 0.0255661
2 FALSE TRUE Dunnett 0.2857143 0.4705882 NA NA -0.3507685 -0.0121601 0.0069943
3 FALSE TRUE Dunnett NA 0.4705882 0.0201567 NA -0.3840376 0.2594915 0.4568425
3 FALSE TRUE Dunnett NA 0.4705882 NA NA NA NA NA
3 FALSE TRUE Dunnett NA 0.4705882 NA NA NA NA NA

Summarizing the results, plot(results, type = 2, legendPosition = 4) produces a plot of the sequence of repeated confidence intervals over the stages:

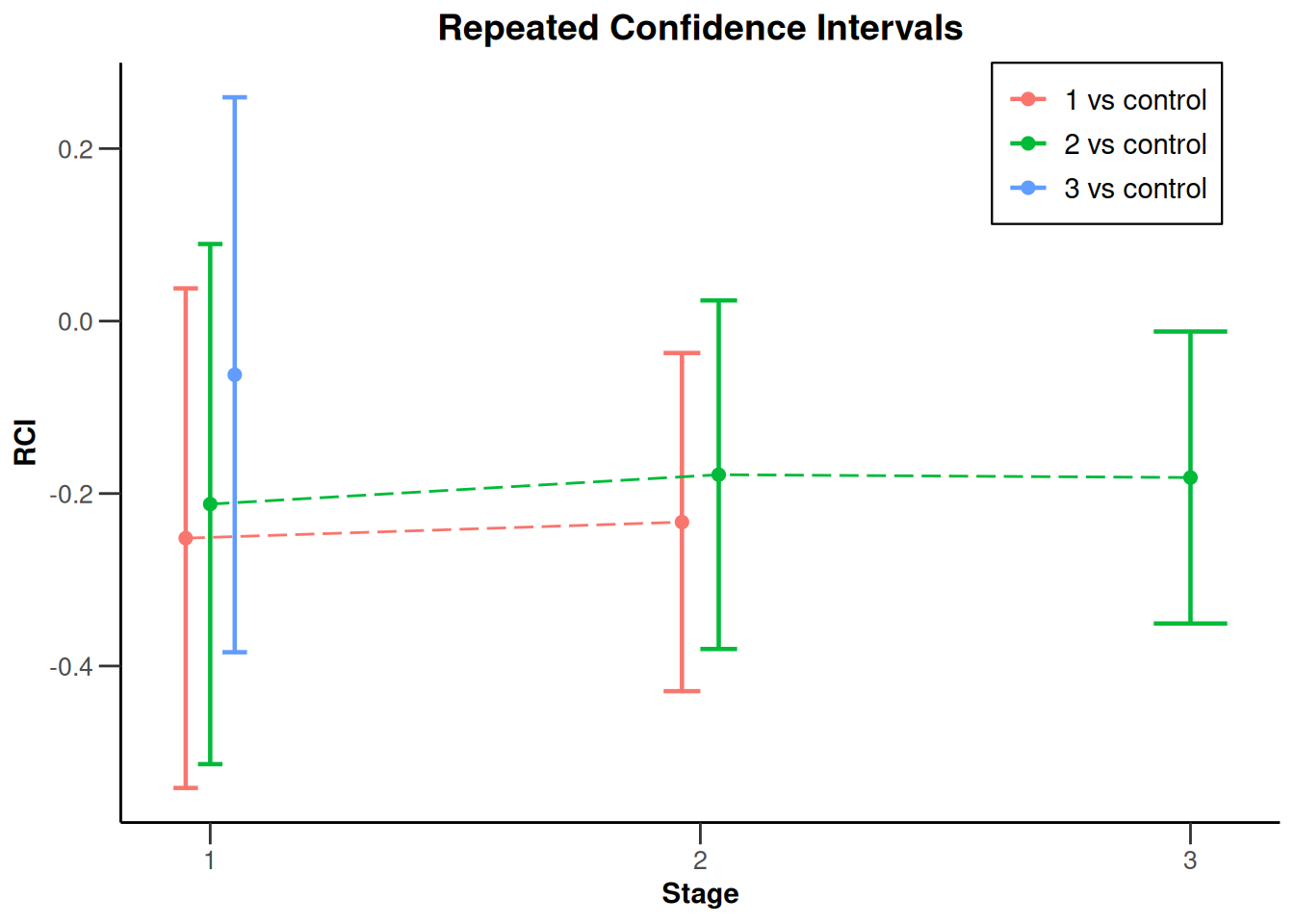
Closing remarks

This example describes a range of design modifications, namely selecting treatments arms and performing sample size recalculation for both stages. It is important to recognize that neither the type of adaptation nor the adaptation rule was pre-specified. Despite this, the closed combination test provides control of the experimentwise error rate in the strong sense. To utilize the whole repertoire of possible adaptations, one might also use the conditional rejection probability (i) values in order to completely redefine the design, which includes, for example, to change the number of remaining stages, to change the type of intersection test, or even to add a treatment arm.

Note that in multi-arm designs no final analysis \(p\)-values, confidence intervals, and median unbiased treatment effect estimates are calculated. This is in contrast to the single hypothesis adaptive designs where, using the stage-wise ordering of the sample space, at the final stage such calculations were done with rpact (for example, see the vignette Analysis of a group sequential trial with a survival endpoint).***

System: rpact 4.0.0, R version 4.3.3 (2024-02-29 ucrt), platform: x86_64-w64-mingw32

To cite R in publications use:

R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. To cite package ‘rpact’ in publications use:

Wassmer G, Pahlke F (2024). rpact: Confirmatory Adaptive Clinical Trial Design and Analysis. R package version 4.0.0, https://www.rpact.com, https://github.com/rpact-com/rpact, https://rpact-com.github.io/rpact/, https://www.rpact.org.